Algoritmy numerickej aproximácie (riešené príklady)

Toto je projekt, na ktorom sa ešte stále pracuje!!

Aj keď sú v tomto dokumente použiteľné informácie, ešte nie je dokončený. Svoje návrhy môžete vyjadriť v diskusii o tejto stránke.

Algoritmy a programovanie - zbierka úloh

Štruktúry

Rekurzia

Dynamická alokácia pamäti

>Algoritmy numerickej interpolácie
>Algoritmy numerickej aproximácie
>Numerické integrovanie
>Numerické derivovanie

Obsah

1 Zadanie
2 Vstupné údaje
- 2.1 Vzorový vstup
- 2.2 Vzorový výstup
3 Analýza matematických vzťahov
4 Analýza programátorského riešenia
- 4.1 Návrh dátových štruktúr
5 Riešenie v jazyku C
- 5.1 Použitie v programe
6 Overenie vypočítaných hodnôt

Zadanie

Riešte problém aproximácie dát. K dispozícii máme n bodov v rovine (ich súradnice x a y). Úlohou bude vypočítať rovnicu aproximujúcej krivky metódou najmenších štvorcov pre:

Lineárnu aproximáciu v tvare [math]y=ax+b[/math]
Logaritmickú aproximáciu v tvare [math]y=a \ln{x} + b[/math]
Exponenciálnu aproximáciu v tvare [math]y=b e^{ax}[/math]
Mocninovú aproximáciu v tvare [math]y=bx^a[/math]

Porovnajte výsledok funkcie s výsledkom v tabuľkovom procesore, kde do (bodového) grafu zo vstupných bodov pridáte spojnicu trendu typu lineárna, resp. logaritmická, mocninová exponenciálna.

Vstupné údaje

Ako vzorku vstupných bodov budeme uvažovať body z intervalu <1,8>. Pre generovanie vstupných hodnôt použijem funkciu [math]f(x)=x^4-exp(x)[/math]

Vzorový vstup

[math]x_i[/math]	[math]y_i[/math]
1.50	0.58
2.00	8.61
3.00	60.91
4.00	201.40
5.00	476.59
6.00	892.57
7.00	1304.37
8.00	1115.04

Vzorový výstup

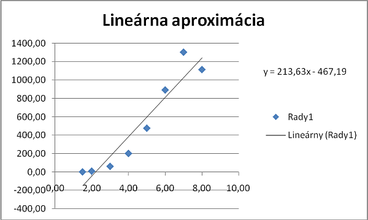
y = 213.634 x - 467.195
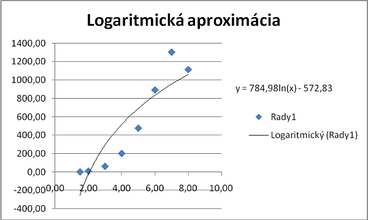
y = 784.982 ln x - 572.83
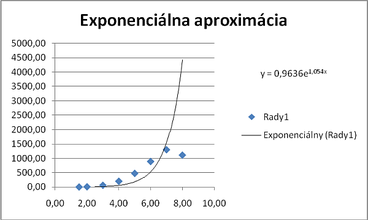
y = 6.9628 e^(1.054x)
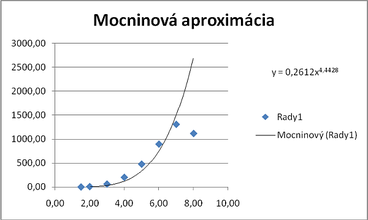
y = 0.2609 x^(4.443)

Analýza matematických vzťahov

Poznámka: v tomto texte nie sú uvádzané celé postupy výpočtu, nakoľko v tomto predmete nie sú primárnym cieľom matematické dôkazy. Študent si postup môže ľahko overiť sám.

Lineárna aproximácia: y=ax+b

Pre lineárnu aproximáciu platia vzťahy:

[math]\begin{align} & b\sum\limits_{i=1}^{n}{{{x}_{i}}}+a\sum\limits_{i=1}^{n}{{{x}^{2}}_{i}}=\sum\limits_{i=1}^{n}{{{x}_{i}}{{y}_{i}}} \\ & nb+a\sum\limits_{i=1}^{n}{{{x}_{i}}}=\sum\limits_{i=1}^{n}{{{y}_{i}}} \\ \end{align}[/math]

Čo môžeme pomocou maticového zápisu zapísať nasledovne:

[math]\left[ \begin{matrix} \sum\limits_{i=1}^{n}{{{x}^{2}}_{i}} & \sum\limits_{i=1}^{n}{{{x}_{i}}} \\ \sum\limits_{i=1}^{n}{{{x}_{i}}} & n \\ \end{matrix} \right]\cdot \left[ \begin{matrix} a \\ b \\ \end{matrix} \right]=\left[ \begin{matrix} \sum\limits_{i=1}^{n}{{{x}_{i}}{{y}_{i}}} \\ \sum\limits_{i=1}^{n}{{{y}_{i}}} \\ \end{matrix} \right][/math]

Riešenie tejto sústavy rovníc je:

[math]\begin{align} & a=\frac{n\sum\limits_{i=1}^{n}{{{x}_{i}}{{y}_{i}}}-\sum\limits_{i=1}^{n}{{{x}_{i}}}\sum\limits_{i=1}^{n}{{{y}_{i}}}}{n\sum\limits_{i=1}^{n}{x_{i}^{2}}-{{\left( \sum\limits_{i=1}^{n}{{{x}_{i}}} \right)}^{2}}} \\ & b=\frac{\sum\limits_{i=1}^{n}{{{y}_{i}}}-a\sum\limits_{i=1}^{n}{{{x}_{i}}}}{n} \\ \end{align}[/math]

Logaritmická aproximácia: [math]y=a*\ln x + b[/math]

Hľadáme najlepšiu aproximáciu pre logaritmickú rovnicu: [math]y=a*\ln x + b[/math]. Postup výpočtu je rovnaký ako v prvom prípade. Jediná zmena v riešení je tá, že os x je v logaritmickej mierke. Dostávame teda sústavu 2 rovníc:

[math]\left[ \begin{matrix} \sum\limits_{i=1}^{n}{{{\left( \ln {{x}_{i}} \right)}^{2}}} & \sum\limits_{i=1}^{n}{\left( \ln {{x}_{i}} \right)} \\ \sum\limits_{i=1}^{n}{\left( \ln {{x}_{i}} \right)} & n \\ \end{matrix} \right]\cdot \left[ \begin{matrix} a \\ b \\ \end{matrix} \right]=\left[ \begin{matrix} \sum\limits_{i=1}^{n}{\left( \ln {{x}_{i}} \right){{y}_{i}}} \\ \sum\limits_{i=1}^{n}{{{y}_{i}}} \\ \end{matrix} \right][/math]

Riešenie tejto sústavy rovníc je:

[math]\begin{align} & a=\frac{n\sum\limits_{i=1}^{n}{\left( \ln {{x}_{i}} \right){{y}_{i}}}-\sum\limits_{i=1}^{n}{\ln {{x}_{i}}}\sum\limits_{i=1}^{n}{{{y}_{i}}}}{n\sum\limits_{i=1}^{n}{{{\left( \ln {{x}_{i}} \right)}^{2}}}-{{\left( \sum\limits_{i=1}^{n}{\ln {{x}_{i}}} \right)}^{2}}} \\ & b=\frac{\sum\limits_{i=1}^{n}{{{y}_{i}}}-a\sum\limits_{i=1}^{n}{\ln {{x}_{i}}}}{n} \\ \end{align}[/math]

Exponenciálna aproximácia: [math]y=b{{e}^{ax}}[/math]

Rovnicu [math]y=b{{e}^{ax}}[/math] si upravíme tak, že ju zapíšeme v logaritmickom tvare:

[math]\begin{align} & \ln y=\ln \left( b{{e}^{ax}} \right) \\ & \ln y=\ln b+\ln {{e}^{ax}} \\ & \ln y=ax+\ln b\,\,\left[ B=\ln b \right] \\ & \ln y=ax+B \\ \end{align}[/math]

Opäť dostávame sústavu 2 rovníc o 2 neznámych. V rovniciach je použitá substitúcia [math]B=\ln b[/math].

[math]\left[ \begin{matrix} \sum\limits_{i=1}^{n}{{{x}^{2}}_{i}} & \sum\limits_{i=1}^{n}{{{x}_{i}}} \\ \sum\limits_{i=1}^{n}{{{x}_{i}}} & n \\ \end{matrix} \right]\cdot \left[ \begin{matrix} a \\ B \\ \end{matrix} \right]=\left[ \begin{matrix} \sum\limits_{i=1}^{n}{{{x}_{i}}\ln {{y}_{i}}} \\ \sum\limits_{i=1}^{n}{\ln {{y}_{i}}} \\ \end{matrix} \right][/math]

Riešenie tejto sústavy rovníc je:

[math]\begin{align} & a=\frac{n\sum\limits_{i=1}^{n}{{{x}_{i}}\ln {{y}_{i}}}-\sum\limits_{i=1}^{n}{{{x}_{i}}}\sum\limits_{i=1}^{n}{\ln {{y}_{i}}}}{n\sum\limits_{i=1}^{n}{x_{i}^{2}}-{{\left( \sum\limits_{i=1}^{n}{{{x}_{i}}} \right)}^{2}}} \\ & B=\frac{\sum\limits_{i=1}^{n}{\ln {{y}_{i}}}-a\sum\limits_{i=1}^{n}{{{x}_{i}}}}{n} \\ \end{align}[/math]

kde [math]B=\ln b[/math].

Mocnimová aproximácia: [math]y=b{{x}^{a}}[/math]

Rovnicu [math]y=b{{x}^{a}}[/math] si upravíme tak, že ju zapíšeme v logaritmickom tvare:

[math]\begin{align} & \ln y=\ln \left( b{{x}^{a}} \right) \\ & \ln y=\ln b+\ln {{x}^{a}} \\ & \ln y=\ln b+a\ln x\,\,\left[ B=\ln b \right] \\ & \ln y=B+a\ln x \\ \end{align}[/math]

Dostávame sústavu 2 rovníc o 2 neznámych. V rovniciach je použitá substirúcia [math]B=\ln b[/math].

[math]\left[ \begin{matrix} \sum\limits_{i=1}^{n}{\ln {{x}_{i}}^{2}} & \sum\limits_{i=1}^{n}{\ln {{x}_{i}}} \\ \sum\limits_{i=1}^{n}{\ln {{x}_{i}}} & n \\ \end{matrix} \right]\cdot \left[ \begin{matrix} a \\ B \\ \end{matrix} \right]=\left[ \begin{matrix} \sum\limits_{i=1}^{n}{\ln {{x}_{i}}\ln {{y}_{i}}} \\ \sum\limits_{i=1}^{n}{\ln {{y}_{i}}} \\ \end{matrix} \right][/math]

Riešením je:

[math]\begin{align} & a=\frac{n\sum\limits_{i=1}^{n}{\ln {{x}_{i}}\ln {{y}_{i}}}-\sum\limits_{i=1}^{n}{\ln {{x}_{i}}}\sum\limits_{i=1}^{n}{\ln {{y}_{i}}}}{n\sum\limits_{i=1}^{n}{{{\left( \ln {{x}_{i}} \right)}^{2}}}-{{\left( \sum\limits_{i=1}^{n}{\ln {{x}_{i}}} \right)}^{2}}} \\ & B=\frac{\sum\limits_{i=1}^{n}{\ln {{y}_{i}}}-a\sum\limits_{i=1}^{n}{\ln {{x}_{i}}}}{n} \\ \end{align}[/math]

kde [math]B=\ln b[/math].

Analýza programátorského riešenia

Návrh dátových štruktúr

V úlohe budeme pracovať s bodmi v rovine, ktoré sú charakterizované x a y súradnicou. Preto si vytvoríme štruktúru Bod, ktorá bude takýto bod reprezentovať:

struct Bod{
   double x,y;
};

V zadaní je úlohou vypočítať rovnicu najlepšie aproximujúcej krivky (lineárnej, logaritmickej, exponenciálnej alebo mocninovej). Tieto krivky sú charakterizované (okrem svojej matematickej funkcie, ktorú vyjadríme neskôr) koeficientami a a b. Na to, aby sme rozlíšili o akú krivku ide, vytvorme si vymenovaný zoznam TYP_KRIVKY, ktorý bude ma 4 symbolické hodnoty:

enum TYP_KRIVKY{
   LIN, LOG, EXP, MOC
};

Význam týchto skratiek si zadefinujme nasledovne:

LIN - lineárna krivka s rovnicou [math]y=ax+b[/math]
LOG - lineárna krivka s rovnicou [math]y=a \ln{x} + b[/math]
EXP - lineárna krivka s rovnicou [math]y=b e^{ax}[/math]
MOC - lineárna krivka s rovnicou [math]y=bx^a[/math]

Teraz si môžeme zadefinovať štruktúru Krivka ako trojicu: typ (TYP_KRIVKY), koeficient a a koeficient b.

struct Krivka{
   TYP_KRIVKY typ;
   double a,b;
};

Riešenie v jazyku C

Vytvoríme funkciu Krivka minSq(Bod *body, int n) kde v poli body sú vstupné údaje, n je počet bodov. Funkcia bude vracať dátovú struktúru typu Krivka, kde budú informácie o tvare aproximujúcej krivky.

 1 Krivka minSq_lin(Bod *body, int n)
 2 {  // y=a+bx
 3    double sx=0,sxx=0,sy=0,sxy=0;
 4     for(int i=0;i<n;i++)
 5     {    sx+=body[i].x;
 6          sy+=body[i].y;
 7          sxy+=body[i].x * body[i].y;
 8          sxx+=body[i].x * body[i].x;
 9     }
10     Krivka k;
11     k.a=(n*sxy-sy*sx)/(n*sxx-sx*sx);
12     k.b=(sy-a*sx)/n;
13     k.typ=LIN;
14     return k;
15 }

Podobným spôsobom môžeme vytvoriť ďalšie 3 funkcie minSq_log, minSq_exp minSq_moc. Ukážeme si ale všeobecnejší tvar funkcie minSq, kde pridáme ďalší parameter, ktorý bude hovoriť aký typ aproximácie sa má vypočítať.

 1 Krivka minSq(Bod *body, int n, TYP_KRIVKY typ_proximacie)
 2 {  
 3    double sx=0,sxx=0,sy=0,sxy=0,slxly;
 4    double slx=0,slxx=0,sly=0,slxy=0,sxly=0;
 5     for(int i=0;i<n;i++)
 6     {    sx+=body[i].x;
 7          slx+=log(body[i].x);
 8          sy+=body[i].y;
 9          sly+=log(body[i].y);
10          sxy+=body[i].x * body[i].y;
11          slxy+=log(body[i].x) * body[i].y;
12          sxly+=body[i].x * log(body[i].y);
13          slxly+=log(body[i].x) *log(body[i].y);
14          sxx+=body[i].x * body[i].x;
15          slxx+=log(body[i].x) * log(body[i].x);
16     }
17     Krivka k;
18     switch(typ_proximacie)
19     {
20       case LIN:
21           k.a=(n*sxy-sy*sx)/(n*sxx-sx*sx);
22           k.b=(sy-k.a*sx)/n;
23           break;
24       case LOG:
25           k.a=(n*slxy-sy*slx)/(n*slxx-slx*slx);
26           k.b=(sy-k.a*slx)/n;
27           break;
28       case EXP:
29           k.a=(n*sxly-sly*sx)/(n*sxx-sx*sx);
30           k.b=(sly-k.a*sx)/n;
31           k.b=exp(k.b);
32           break;
33       case MOC:
34           k.a=(n*slxly-sly*slx)/(n*slxx-slx*slx);
35           k.b=(sly-k.a*slx)/n;
36           k.b=exp(k.b);
37           break;
38     }
39     k.typ=typ_proximacie;
40     return k;
41 }

Použitie v programe

Pre názornosť nebudeme v programe dáta načítavať z klávesnice, ale vstupné údaje budú zadané priamo v zdrojovom kóde. Modifikácia zdrojového kódu s načítaním vstupných hodnôt je jednoduchá a určite ju každý zvládne sám.

V zdrojovom kóde pribudla ešte funkcia vypisRovnicuKrivky, ktorá vypíše rovnicu krivky v čitateľnom tvare pre človeka. Vo výpise sú vynechané všetky funkcie, ktoré sú boli v tomto príklade vysvetlené a ich zdrojový kód bol napísaný skôr.

 1 #include <iostream.h>
 2 #include <conio.h>
 3 #include <math.h>
 4 
 5 struct Bod {double x,y;};
 6 enum TYP_KRIVKY{ LIN, LOG, EXP, MOC};
 7 struct Krivka{
 8    TYP_KRIVKY typ;
 9    double a,b;
10 };
11 
12 //Krivka minSq(Bod *body, int n, TYP_KRIVKY typ_proximacie)
13 
14 void vypisRovnicuKrivky(Krivka k)
15 {
16    cout<<"y=";   
17    switch(k.typ)
18    {
19       case LIN:
20            cout<<k.a<<" x";
21            if(k.b>0) cout<<"+";
22            cout<<k.b;
23           break;
24       case LOG:
25            cout<<k.a<<" ln x";
26            if(k.b>0) cout<<"+";
27            cout<<k.b;
28           break;
29       case EXP:
30            cout<<k.b<<" e^(";
31            cout<<k.a<<" x)";
32           break;
33       case MOC:
34            cout<<k.b<<" x^(";
35            cout<<k.a<<" )";
36           break;
37     }     
38 }
39 int main()
40 {  const int n=8;
41    Bod body[n]={
42       {1.50,0.58},
43       {2.00,8.61},
44       {3.00,60.91},
45       {4.00,201.40},
46       {5.00,476.59},
47       {6.00,892.57},
48       {7.00,1304.37},
49       {8.00,1115.04}		
50    }; 
51   Krivka Q;
52   Q=minSq(body,n,EXP); // LOG, LIN, EXP
53   vypisRovnicuKrivky(Q);
54   getch();
55 }

Overenie vypočítaných hodnôt

V nasledujúcich obrázkoch sú vstupné body z príkladu znázornené v tabuľkovom procesore a je vypočítaná najlepšia aproximujúca krivka (MS Excel ju nazýva spojnica trendu).

Algoritmy numerickej aproximácie (riešené príklady)

Obsah

Zadanie

Vstupné údaje

Vzorový vstup

Vzorový výstup

Analýza matematických vzťahov

Lineárna aproximácia: y=ax+b

Logaritmická aproximácia: [math]y=a*\ln x + b[/math]

Exponenciálna aproximácia: [math]y=b{{e}^{ax}}[/math]

Mocnimová aproximácia: [math]y=b{{x}^{a}}[/math]

Analýza programátorského riešenia

Návrh dátových štruktúr

Riešenie v jazyku C

Použitie v programe

Overenie vypočítaných hodnôt

Navigačné menu

Osobné nástroje

Menné priestory

Varianty

Zobrazenia

Viac

Hľadať

Navigácia

Rýchle linky

Nástroje