Aplikácie teórie grafov a teórie hier v rozhodovacích problémoch

|
Trenčianska Univerzita Alexandra Dubčeka v Trenčíne
Fakulta Mechatroniky |

|
| Autor: | Ľubomír Milko
|
| Pedagogický vedúci: | Ing. Juraj Ďuďák |
| Študijný odbor: | Mechatronika
|
| Akademický rok | 2009/2010
|
Obsah
| Abstrakt
Táto práca obsahuje charakteristiku teórie hier a teórie grafov a následne popisuje použitie princípov z tejto oblasti v základných druhoch rozhodovacích problémov. Vo štvrtej kapitole sa podrobnejšie opisujú princípy analýzy a riešenia hier, ktoré môžu byť reprezentované hernými stromami. Posledná časť práce je venovaná implementácii rozobraných princípov voľby vhodného ťahu v doskovej hre dáma. |
| Abstract
tu bude anstrakt v AJ |
Úvod
Problémy vyžadujúce správne rozhodovanie s ohľadom na následky zvoleného rozhodnutia nás sprevádzajú v takmer všetkých oblastiach ľudskej činnosti od hrania rôznych spoločenských hier až po pokročilé riadenie cestnej siete, správne ekonomické rozhodnutia alebo stratégiu vojenských konfliktov. Postupné snahy o matematickú interpretáciu a riešenie týchto problémy voľby správneho rozhodnutia vyústili v samostatné odvetvie aplikovanej matematiky s názvom teória hier. V tejto teórii sa rozhodovacie problémy znázorňujú ako množina stratégií, ktoré možno prijať a množina následkov, ktoré vzniknú v dôsledku zvolenej stratégie. Následky sú často číselnou interpretáciou daného stavu. Na praktickú interpretáciu tohto súboru množín sa využíva teória grafov. Tieto dve teórie možno použiť na vyriešenie mnohých praktických rozhodovacích problémov. Zaujímavým praktickým a názorným príkladom aplikácie môže byť aj hľadanie optimálneho ťahu v doskových hrách akou je napríklad dáma. Súčasťou tejto práce je teda aj podrobnejšia ukážka využitia teórie hier a teórie grafov v tomto type hier. Cieľom tejto práce potom je:
- charakteristika teórie hier a teórie grafov,
- popis interpretácie základných rozhodovacích problémov pomocou týchto teórií,
- praktické použitie popísaných teoretických princípov pri voľbe vhodného ťahu v doskovej hre dáma.
Zoznam použitých skratiek a symbolov
- hra
- strategická interakcia medzi jednotlivcami
- hráč
- účastník hry
- minimax
- algoritmus, ktorý prechádzaním herného stromu vyberá optimálny ťah v hre
- pozícia
- aktuálny stav hry
- strom
- typ grafu, využívaný na znázornenie hier v rozšírenej forme
- ťah
- zvolená a uskutočnená stratégia hráča v danom bode hry
Teória hier
Základné pojmy a charakteristika teórie hier
Teória hier je odvetvím aplikovanej matematiky, ktorá sa snaží matematicky zachytiť správanie v strategických situáciách, kde úspech jednotlivca pri vykonaní určitej voľby závisí od volieb ostatných [1].
Súbor situácií, v ktorých sa každý účastník môže nachádzať je v teórii hier nazývaný hra. Hra je akousi strategickou interakciou medzi jednotlivcami. Každý účastník (prvok, ktorý sa aktívne zúčastňuje hry) je označený ako hráč. Každý hráč má v daných momentoch možnosť voľby akcie, ktorá ďalej ovplyvní priebeh hry. Každá z možných akcií, ktoré hráč môže vykonať sa označuje ako ťah. Súbor ťahov, ktoré hráč použije v hre je označovaný ako stratégia.
Teória hier skúma predpokladané a skutočné správanie sa hráčov v hrách, rovnako ako aj optimálne stratégie. Zdanlivo odlišné typy interakcií medzi hráčmi a hrou sa môžu prejavovať podobnými štruktúrami pohnútok, takže všetky môžu byť reprezentované ako príklady jednej konkrétnej hry. V počiatkoch bola teória hier rozvíjaná na analyzovanie súťaží (situácií), kde každému hráčovi sa darilo lepšie na úkor ostatných [1]. Jedná sa o tzv. hry s nulovým súčtom. Išlo napr. o analýzu rôznych vojenských konfliktov, prípadne spoločenských hier. Neskôr sa teória hier rozšírila na analyzovanie širokého spektra interakcií, ktoré sú klasifikované podľa niekoľkých kritérií. Dnes pojem teória hier zahŕňa množstvo teórií, ktoré možno aplikovať v rôznych rozhodovacích problémoch, kde hráčmi môžu byť ľudia, počítače, zvieratá, rastliny, atď.
Tradičné aplikácie teórie hier sa snažia v hrách nájsť stav rovnováhy. To znamená nájsť súbor stratégií, kde je nepravdepodobné, že jednotlivé prvky budú meniť svoje správanie. Na riešenie týchto problémov bolo vyvinutých veľa konceptov, z ktorých najznámejšia je Nashova rovnováha [1].
Nashova rovnováha
Je to koncept riešenia hier zahŕňajúcich dvoch alebo viac hráčov, kde každý hráč pozná stratégie rovnováhy (teda najlepšie stratégie, aké môžu zvoliť ostatní, aby získali čo najviac) ostatných hráčov a žiadny hráč nemá čo získať zmenou iba svojej vlastnej stratégie. Ak každý hráč zvolil stratégiu a žiadny hráč nemôže profitovať zmenou svojej stratégie, pokiaľ ostatní hráči ponechajú svoje stratégie nezmenené, potom daný súbor strategických rozhodnutí a odpovedajúcich odmien stanovuje Nashov stav rovnováhy. Inými slovami, byť v Nashovom stave rovnováhy znamená, že každý hráč odpovie negatívne na otázku : “Ak s určitosťou poznám stratégie ostatných hráčov, môžem profitovať zmenou mojej stratégie ?“ [1]. Jedným z najznámejších typov takejto hry je napr. väzňova dilema spopularizovaná matematikom Albertom W. Tuckerom.
Väzňova dilema
Opis problému je nasledovný: Dvaja väzni vykradli banku a boli neskôr chytení políciou. Vo väzení ich zavrú do samostatných ciel. Väzni nemajú možnosť spolu komunikovať. Polícia nemá dosť dôkazov aby uväznila oboch. Obaja dostanú od polície ponuku spolupracovať (zradiť komplica), výmenou za nízky trest pre seba. Možné výsledky sú takéto:
- Ak budú obaja navzájom spolupracovať, budú ich držať najviac rok vo vyšetrovacej väzbe.
- Ak jeden z väzňov zradí komplica, pustia ho ihneď na slobodu, ale komplic dostane 10 rokov väzenia.
- Ak sa priznajú/zradia obaja, rozdelia si 10 ročný trest, čiže každý dostane 5 rokov.
Z hľadiska skupinového správania sa je najvýhodnejšie riešenie ak obaja spolupracujú, pretože vtedy je celkový čas ktorý obaja strávia vo väzení najmenší. Z hľadiska sebeckého správania sa každého z nich je najjednoduchšie priznať sa, pretože tak môže dostať v horšom prípade 5 rokov, oproti možnostiam 1 alebo 10 rokov ak sa neprizná [11].
Stručný vývoj teórie hier
Prvá známa zmienka o teórii hier sa vyskytla v liste z roku 1713 napísanom Jamesom Waldegraveom. V tomto liste Waldegrave navrhol tzv. zmiešanú minimax stratégiu ako riešenie kartovej hry pre dvoch hráčov nazývanej “le Her”. Neskôr roku 1838 využil hernú teoretickú analýzu Antoine Augustin Cournot vo svojej knihe Výskumy matematických princípov teórie bohatstva. V tejto svojej práci Cournot pojednáva o duopoloch a prezentuje riešenie, ktoré je obmedzenou verziou Nashovej rovnováhy.
Hoci bola Cournotova analýza viac všeobecná ako Waldegraveova, teória hier stále neexistovala ako samostatná oblasť vedy, až pokiaľ John von Neumann, ktorý je považovaný za zakladateľa teórie hier, nepublikoval sériu prác na túto tému v roku 1928. Neskôr, v roku 1944, Von Neumann spolu s Oskarom Morgensternom vydal knihu Teória hier a ekonomické správanie. Táto kniha obsahuje metódy hľadania riešení hier dvoch hráčov s nulovým súčtom. Počas tohto obdobia bola teória hier primárne zameraná na teóriu kooperatívnych hier, ktorá analyzovala optimálne stratégie pre skupiny jednotlivcov za predpokladu, že môžu medzi sebou presadiť dohodu o vhodnej spoločnej stratégii.
V roku 1950 sa objavila prvá zmienka o väzňovej dileme a organizácia RAND (Research ANd Development) podnikla experiment na základe tejto hry. V tomto čase aj John Nash vyvinul kritérium pre vzájomnú koexistenciu stratégie hráčov, známe ako Nashova rovnováha. Toto kritérium možno aplikovať na širšie spektrum hier, než kritérium, ktoré navrhli Neumann a Morgenstern. Toto kritérium je dostatočne univerzálne a umožňuje analýzu kooperatívnych aj nekooperatívnych hier.
Teória hier zaznamenala náhly vzostup v 50-tych rokoch, kedy boli vymyslené nové herné koncepty ako napríklad: jadrá, rozšírená forma hier, fiktívne hry, atď. V tomto období sa aj objavili prvé aplikácie teórie hier vo filozofii a politike.
V roku 1956 Reinhard Selten uviedol svoj koncept riešenia tzv. perfektnej rovnováhy v určitej podmnožine hry, ktorá vylepšila Nashovu rovnováhu.
V 70-tych rokoch bola teória hier výrazne aplikovaná v biológii, hlavne ako dôsledok práce Johna Maynarda Smitha a jeho evolučne stabilnej stratégie. Navyše boli uvedené a analyzované ďalšie koncepty rozširujúce teóriu hier.
V roku 2005, herní teoretik Thomas Schelling získal Nobelovu cenu za prácu na dynamických modeloch, ktoré boli prvotnými ukážkami evolučnej hernej teórie.
V roku 2007 boli Roger Myerson, spolu s Leonidom Hurwiczom a Ericom Maskinom ocenení Nobelovou cenou za ekonomiku za položenie základov teórie dizajnu mechanizmov hier.
Oblasti využitia teórie hier
Teória hier bola využívaná hlavne na štúdium správania ľudí a zvierat. Primárne bola rozvíjaná v ekonomike na pochopenie rôznych druhov ekonomického správania, zahŕňajúcich správanie firiem, trhu a zákazníkov. Postupne sa využitie teórie hier v spoločenských vedách zväčšovalo a poznatky z teórie hier sa začali aplikovať aj na politické, sociologické a psychologické javy.
Hernú teoretickú analýzu spočiatku využíval Ronald Fisher na štúdium správania zvierat v 30-tych rokoch (hoci ešte predtým urobil k tejto téme niekoľko neformálnych vyjadrení Charles Darwin). Neskôr boli analytické metódy, ktoré využíval aj Fisher pomenované teória hier. Výsledky rozvoja tejto oblasti v ekonomike boli neskôr rozsiahlo aplikované v biológii Johnom M. Smithom v jeho knihe Evolúcia a teória hier.
Poznatky z teórie hier sa využívajú aj na predpovedanie a vyloženie etického a normatívneho správania. Vo filozofii sa teória hier aplikovala na pochopenie dobrého alebo správneho správania. Počiatky využitia teórie hier na tomto poli môžu byť datované až do čias Platóna.
Prvotné aplikácie teórie hier v politických vedách je možno nájsť v práci Anthonyho Downsa. Významnou je napr. jeho kniha Ekonomická teória demokracie (1957).
V ekonomike je teória hier využívaná na analýzu veľkého množstva ekonomických javov ako napr. trh, aukcie, výpredaje, duopoly, oligopoly, sociálna sieť a volebné systémy. Tento výskum sa zvyčajne zameriava na určitý súbor stratégií známych ako equilibrium (rovnováha) v hrách. V nekooperatívnych hrách je najznámejším z týchto konceptov spomínaná Nashova rovnováha.
V posledných rokoch zohráva teória hier významnú úlohu aj v počítačových vedách a logike. Hry sú napr. využívané na modelovanie interaktívnych výpočtov.
Využitie teórie hier však možno nájsť aj v telekomunikáciách, doprave, psychológii, vojenských vedách, hazarde a mnohých iných oblastiach.
Spôsoby reprezentácie rozhodovacích problémov
Hry skúmané v teórii hier sú dobre definovateľnými matematickými objektmi. Hra pozostáva zo súboru hráčov, súboru ťahov (alebo stratégií), ktoré môžu hráči vykonať a daného ohodnotenia, pre každú kombináciu stratégií. Pre nekooperatívne hry , kde hráči navzájom nemôžu spolupracovať sa využíva rozšírená alebo normálna forma reprezentácie hry. Kooperatívne hry sú často reprezentované charakteristickou funkciou.
Rozšírená forma
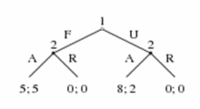
Rozšírená forma môže byť použitá na opis hier s určitým dôležitým poradím vykonávania jednotlivých ťahov (stratégií). Takéto hry sú často reprezentované ako herné stromy. Každý vrchol (uzol) tu predstavuje rozhodovací bod hráča. Hráč je označený číslom pri každom vrchole. Čiary smerujúce z každého vrcholu reprezentujú možnú akciu (ťah) príslušného hráča. Odmeny (hodnotenie) hráčov sú reprezentované na konci posledných spodných čiar.
V hre znázornenej na obrázku 1 sú dvaja hráči. Hráč 1 začína a má možnosti F alebo U. Hráč 2 vidí ťah Hráča 1 a vyberá si medzi ťahmi A a R. Ak uvažujeme, že Hráč 1 vyberie U a Hráč 2 zvolí možnosť A, potom Hráč 1 získa hodnotenie 8 a Hráč 2 získa hodnotenie 2.
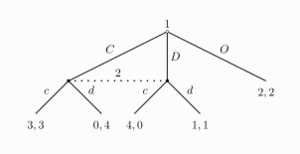
Rozšírenou formou sa dajú zachytiť aj hry so simultánnym pohybom a hry s neúplnou informáciou. V takomto prípade buď bodkovaná čiara spája uzly na znázornenie, že sa jedná o rovnaký súbor informácií (teda, že hráči nevedia, v ktorom bode sa nachádzajú) alebo je okolo takýchto uzlov nakreslená uzavretá čiara [1].
Normálna forma
Normálna (alebo strategická) forma hry je reprezentovaná maticou, ktorá zobrazuje hráčov, stratégie a odmeny. Pre každú kombináciu ťahov (stratégií) priraďuje zodpovedajúce ohodnotenie (odmenu) každému z hráčov. V tabuľke 1 je znázornená tzv. väzňova dilema. Väzeň 1 vyberá svoju stratégiu jednania z riadkov a väzeň 2 zo stĺpcov. Každý z väzňov má na výber dve stratégie, reprezentované dvomi riadkami a dvomi stĺpcami. Vo vnútri buniek sú zapísané počty rokov (odmena) , ktoré budú musieť stráviť vo väzení pri zvolených stratégiách . Nevýhodné odmeny sú zvyčajne pre upresnenie zapísané zápornou hodnotou. Prvé číslo znázorňuje odmena väzňa 1, druhé číslo je odmena väzňa 2.
Za predpokladu, že väzeň 1 zvolí možnosť spolupracovať a väzeň 2 bude tiež spolupracovať získajú obaja ohodnotenie -1. Ak je hra reprezentovaná touto formou predpokladá sa, že hráči vykonávajú svoje ťahy (stratégie) súčasne alebo prinajmenšom nepoznajú ťah súpera. V opačnom prípade sa hry znázorňujú rozšírenou formou.
Forma charakteristickej funkcie
Využíva sa pri kooperatívnych hrách, kde nie sú určené žiadne individuálne odmeny pre hráčov. Namiesto toho charakteristická funkcia definuje ohodnotenie každého spojenectva. Štandardným predpokladom je že prázdna koalícia získa ohodnotenie 0.
Pôvod tejto formy pochádza z knihy von Neumanna a Morgensterna, ktorí pri štúdiu koaličných hier vyjadrených normálnou formou usúdili, že ak sa vytvorí koalícia K, hrá proti inej koalícii N (N\K) rovnako ako keby sa hrala hra dvoch hráčov. Existujú rôzne modely odvodenia koaličných odmien z normálnej formy hry, ale nie všetky hry v charakteristickej forme môžu byť odvodené z hier určených normálnou formou.
Formálne je hra určená formou charakteristickej funkcie daná dvojicou (N,ϑ), kde N označuje súbor hráčov a ϑ:2^N→R je charakteristická funkcia [1].
Forma rozdeľujúcej funkcie
Rozšírenie formy charakteristickej funkcie, kde odmena koalície nezávisí iba na jej členoch, ale tiež na spôsobe akým sú rozdelení ostatní hráči [1].
Typy hier
Kooperatívne a nekooperatívne hry
Hra je kooperatívna ak hráči majú možnosť vytvoriť medzi sebou určité zväzky - koalície. V takomto druhu hier sa od hráčov vyžaduje dodržanie týchto ich záväzkov. V nekooperatívnych hrách sa takéto záväzky nedodržiavajú. Často je tiež v kooperatívnych hrách usudzované, že hráči môžu navzájom komunikovať (teda, že vedia navzájom o svojich stratégiách vo vytvorenom zväzku). Pri nekooperatívnych hrách je na druhú stranu väčšinou možné modelovať situácie do najmenších detailov a vyvodzovať presné dôsledky. Kooperatívne hry sa sústreďujú na hru ako celok. Určitým spojením medzi kooperatívnymi a nekooperatívnymi hrami sú tzv. hybridné hry, ktoré obsahujú elementy z oboch typov [1].
Symetrické a asymetrické hry
Symetrické hry sú také, kde odmeny (ohodnotenia) za zvolenie určitej stratégie závisia iba od ostatných stratégií, ktoré zvolia ostatní hráči a nie od toho, kto volí danú stratégiu. Inak povedané, ak môžeme zameniť hráčov a odmeny budú stále rovnaké, potom hra je symetrická. Väčšina bežne študovaných hier 2x2 je symetrická. Príkladom je napr. väzňova dilema. Tabuľka 2 je ukážka symetrickej hry v normálnej forme.
Väčšina asymetrických hier sú hry, kde hráči nemajú na výber rovnaké stratégie. Je tiež ale možné, že hra, ktorá má pre oboch hráčov stratégie identické, nie je symetrická. Takéto hry sa líšia v ohodnotení stratégií v závislosti od toho, aký hráč danú stratégiu vykonal [1].
Hry s nulovým a nenulovým súčtom
Hry s nulovým súčtom sú špeciálnym typom hier s konštantným súčtom, v ktorých voľby hráčov nemôžu ani zvýšiť a ani znížiť zdroje, ktoré sú k dispozícii. V hrách s nulovým súčtom je celkové ohodnotenie všetkých hráčov vždy rovné nule (hráč môže profitovať iba na adekvátny úkor ostatných). Príkladom takýchto hier sú aj doskové spoločenské hry ako šach, dáma alebo napr. poker. Tabuľka 3 znázorňuje hru dvoch hráčov s nulovým súčtom.
Mnoho hier však sú hry s nenulovým súčtom (vrátane väzňovej dilemy). Zisk jedného hráča tu nemusí nutne znamenať stratu hráča druhého.
Hry s konštantným súčtom zodpovedajú javom ako krádeže a hazardné hry, ale nie základným ekonomickým princípom, kde je možné potenciálne nadobudnúť zisk z obchodu [1].
Simultánne a ťahové (sekvenčné) hry
Simultánne hry sú také, pri ktorých hráči vykonávajú svoje stratégie (ťahy) súčasne alebo ak neťahajú súčasne, tak hráči, ktorí sú na ťahu neskôr nevedia o predošlých akciách svojich súperov.
V sekvenčných hrách majú tzv. neskorší hráči určité poznatky o predošlých akciách ostatných. Tieto poznatky však môžu byť len veľmi obmedzené. Môžu byť napr. informovaní len o tom, že nejaký hráč nevykonal určitú stratégiu, no nevedia, ktorú z možných stratégií vykonal. Na reprezentáciu simultánnych hier sa často volí normálna forma a na reprezentáciu sekvenčných rozšírená forma [1].
Hry s úplnými a neúplnými informáciami
Hry s úplnými informáciami sú dôležitou podmnožinou sekvenčných hier. Pri hrách s úplnými informáciami všetci hráči vedia o všetkých predošlých ťahoch ostatných hráčov. To znamená, že takýmto druhom hier nemôžu byť simultánne hry, pri ktorých už z princípu ostatní hráči nevedia o všetkých predošlých akciách svojich spoluhráčov.Väčšina hier analyzovaných v hernej teórii sú však hry s neúplnou informáciou. Hry s úplnou informáciou predstavujú aj rôzne doskové spoločenské hry ako napr. šach, Go, dáma a iné.
Hry s úplnými informáciami bývajú často zamieňané s hrami s kompletnými informáciami, čo sú hry, pri ktorých každý hráč pozná stratégie a ohodnotenia ostatných hráčov, nemusí však vedieť o tom aké akcie vykonali, teda, ktoré stratégie zvolili. Obrázok 2 ukazuje znázornenie hry s neúplnými informáciami v rozšírenej forme.
Nekonečne dlhé hry
Hry analyzované ekonómami a reálnymi hráčmi sú obecne ukončené po určitom konečnom počte krokov. V matematike a teórii množín však sú objektom štúdia aj hry, ktoré trvajú nekonečný počet ťahov s víťazom (alebo daným ohodnotením) známym až po ukončení všetkých ťahov.
Záujem sa v takomto prípade hier nesústreďuje ani tak na najoptimálnejší spôsob hry ako zisťovanie, či pre určitého hráča existuje alebo neexistuje tzv. výherná stratégia. Existencia takýchto stratégií má významné dôsledky v deskriptívnej teórii množín [1].
Metahry
Sú to hry, ktorých hra znamená rozvoj pravidiel, cieľa alebo predmetu inej hry. Metahry sa snažia o maximalizovanie praktickej hodnoty vyvinutého súboru pravidiel. Teória metahier je spojená s dizajnom mechanizmov hier [1].