Aplikácia stromov a princípov z teórie hier v niektorých ťahových hrách

Obsah práce

1.	Teória hier
2.	Teória grafov
3.	Aplikácia stromov a princípov z teórie hier v niektorých ťahových hrách
4.	Implementácia algoritmov z teórie hier a teórie grafov do spoločenskej hry dáma

Aplikácia stromov a princípov z teórie hier v niektorých ťahových hrách

Herné stromy

Obr. 11 – Ukážka herného stromu pre hru piškvorky

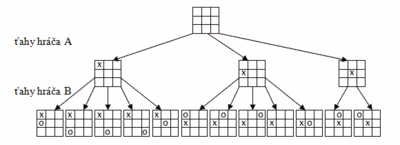
Herné stromy sú najčastejšie využívaným variantom reprezentácie väčšiny jednoduchších spoločenských hier. V teórii hier sa takýto popis označuje ako rozšírená forma. Herný strom tvorí orientovaný graf, ktorého vrcholy (uzly) predstavujú jednotlivé pozície v hre (rozloženie na hernej doske) a orientované hrany reprezentujú jednotlivé ťahy (polťahy). Pri hrách pre dvoch hráčov jeden ťah pozostáva z dvoch polťahov, pričom polťah je ťah vykonaný jedným z hráčov. Strom potom pozostáva z vrstiev vrcholov (pozícií), ktoré sa postupne zväčšujú v závislosti od zložitosti hry. Jednotlivé vrcholy vznikajú ako následok všetkých možných polťahov striedavo vždy od jedného z hráčov. Na obr. 11 (prebraný z ) je ukážka časti herného stromu pre hru piškvorky. Tento strom má hĺbku dva polťahy. Kvôli jednoduchosti sú uvedené len varianty možných ťahov (stred okraja, vrchol, stred hracieho poľa). Inak by boli jednotlivé vrstvy pozícií podstatne rozsiahlejšie (už druhá vrstva by obsahovala 9 rôznych pozícií, pretože hráč môže v skutočnosti urobiť ťah na jedno z 9 políčok).

Úplný herný strom predstavuje celý priebeh hry od začiatku až do konca. Východiskový (koreňový) vrchol úplného herného stromu teda reprezentuje počiatočnú pozíciu hry. Z neho potom vychádzajú orientované hrany jednotlivých polťahov, ktoré smerujú do vrcholov, ktoré potom predstavujú zmenené pozície po vykonaní ťahu. Koncové vrcholy, tzv. listové vrcholy, sú v úplnom strome tvorené všetkými možnými koncovými pozíciami v hre. Tvoria ich teda všetky výherné (pre jedného alebo druhého hráča) a remízové pozície. Úlohou hráča je potom vykonať takú sekvenciu ťahov, ktorá povedie až k pre neho výhernému listovému vrcholu, prípadne k remíze.

Riešenie herných stromov

Obr. 12 – Úplný farebný herný strom

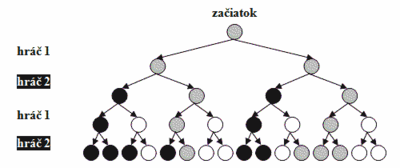
Riešením herného stromu je nájdenie postupnosti ťahov, ktoré určite povedú k výhre alebo remíze (každý hráč ma svoje riešenie herného stromu). Princíp nájdenia takejto sekvencie ťahov môžeme opísať pomocou úplného farebného herného stromu (Obr. 12). V hre, ktorú znázorňuje tento strom môže každý hráč vykonať vždy len dva ťahy.

Postup vyfarbenia jednotlivých vrcholov je rekurzívny, pretože začína od listových vrcholov (uzlov), ktoré predstavujú konečné pozície hry. Algoritmus vyfarbovania je nasledujúci:

1. Vyfarbi poslednú vrstvu pozícií (listové vrcholy). Čierna farba znamená výhru pre prvého hráča. Biela označuje výhru druhého hráča. Remíza je vyznačená šedou farbou.
2. Prejdi do vyššej vrstvy. Ak je niektorý z vrcholov v najbližšej nižšej vrstve zafarbený opačne ako farba hráča, ktorý bol naposledy na ťahu, zafarbi aj aktuálny vrchol touto farbou protihráča. Nadradený vrchol potom bude rovnakej farby ako je farba hráča, ktorý je aktuálne na ťahu. Ak sú oba najbližšie nižšie vrcholy zafarbené rovnakou farbou jedného z hráčov, zafarbi aj aktuálny vrchol touto farbou. Inak vyfarbi aktuálny vrchol ako remízu.
3. Rovnakým postupom ako v bode č. 2 vyfarbi všetky vrcholy smerom nahor. Koreňový vrchol potom predstavuje povahu hry (v našom prípade je hra neutrálna, teda obaja hráči majú možnosť výhry).

Každá zo sekvencie vrcholov, ktoré vedú k vyriešeniu hry (k víťazstvu alebo remíze) sa nazýva rozhodovací strom. Veľkosť (rozmer) rozhodovacieho stromu je daná počtom listových vrcholov. Veľkosťou a tvarom rozhodovacích stromov sa určuje komplexnosť hier a ich vlastnosti.

Ohodnocovanie pozícií v hernom strome

Na určenie vhodnej postupnosti ťahov vedúcich k určitému víťazstvu (príp. remíze) nutne potrebujeme poznať úplný herný strom. Bez listových vrcholov s koncovými pozíciami hry totiž nevieme k akému konečnému stavu môže viesť určitý ťah. Vytvorenie úplného herného stromu je však, až na pár výnimiek, pre väčšinu hier príliš zdĺhavé a vo veľa prípadoch prakticky nemožné. V hre piškvorky (na 9 políčkach) napríklad môže vzniknúť 5478 rôznych legálnych pozícií. Po odčítaní otočených a zrkadlových pozícií ich však je len 765. Oproti tomu v dáme je legálny počet pozícií odhadovaný na 10²⁰. Šach môže mať takýchto pozícií približne 10⁴⁰. Pri určení nasledujúceho optimálneho ťahu z danej pozície teda budeme musieť v drvivej väčšine prípadov vychádzať z neúplného herného stromu. Postup je principiálne rovnaký ako pri ukážkovej metóde vyfarbovania, avšak listy stromu nie sú koncovými pozíciami hry a okrem rozhodovania úvodného ťahu, nesymbolizuje ani koreňový uzol počiatočnú pozíciu. Keďže teda nevieme či sa bude jednať o výhru jedného alebo druhého hráča alebo pôjde o remízu, musíme nejakým spôsobom zhodnotiť stav hry v listovom vrchole a z neho potom rekurzívne metódou principiálne zhodnou s vyfarbovaním určiť nasledujúci optimálny ťah z koreňového uzla. Najbežnejším spôsobom je ohodnotenie každej listovej pozície určitou číselnou hodnotou. Táto hodnota potom reprezentuje celkový stav hry v danej pozícii, pričom pre jedného z hráčov je výhodné ak je táto hodnota čo najvyššia a pre druhého zase opačne. Ohodnotenie potom vzniká tak, že sa najprv ohodnotí pozícia kladne len z hľadiska jedného hráča a potom záporne z hľadiska druhého hráča. Tieto ohodnotenia sa potom sčítajú a vznikne celkové ohodnotenie pozície. Z toho vyplýva, že nerozhodný stav hry je ohodnotený číslom nula. Ohodnotenie pozície je závislé na pravidlách hry. Pri dáme je napr. možné hodnotiť počty figúrok (napr. každá figúrka má hodnotu 10).

Algoritmus minimax

Všeobecný popis

Obr. 13 – Princíp algoritmu minimax

Minimaxová metóda je jednou z najčastejšie využívaných metód pri hľadaní optimálnych ťahov v ohodnotenom hernom strome. Minimax využíva hlavnú devízu počítačov a to ich rýchlosť a pamäť. Jedná sa teda o algoritmus, ktorý používa hrubú silu k nájdeniu optimálneho ťahu z danej pozície. Rôzne upravené a optimalizované formy tohto algoritmu sú použité v drvivej väčšine šachových a podobných programov. Existujú aj iné techniky, ktoré sa snažia viac napodobniť ľudské myslenie (neurónové siete, evolučné algoritmy), no minimaxová metóda je zatiaľ najúčinnejšia. Názov minimax vznikol podľa princípu ohodnocovania jednotlivých vrcholov v hernom strome, kde jeden hráč si volí tie pozície, ktoré sú ohodnotené čo najvyššie (tento hráč maximalizuje) a druhý hráč si volí pozície, ktoré majú ohodnotenie čo najnižšie (minimalizuje). Pri hrách s viacerými hráčmi je samozrejme situácia komplikovanejšia. Pritom sa predpokladá, že obaja hráči uskutočnia vždy pre nich ten najlepší možný ťah.

Princíp algoritmu minimax

Algoritmus najprv prechádza od koreňového vrcholu herného stromu postupne až k listomlistom (generuje sa herný strom), ktoré sa ohodnotia ohodnocovacou funkciou. Listové vrcholy sú určené hĺbkou prehľadávania, ktorá definuje počet vrstiev herného stromu (pri hĺbke 5 má herný strom 5 vrstiev, kde vrcholy poslednej vrstvy sú považované za listové). Ak je vygenerovaná pozícia (teda vrchol v hernom strome), ktorá znamená koniec hry ešte pred dosiahnutím danej hĺbky, je aj takýto vrchol považovaný za listový. Alternatívou k priamemu určeniu hĺbky prehľadávania je určenie časovej konštanty, ktorá určuje ako dlho môže herný strom zväčšovať počet svojich úrovní.

Po ohodnotení listových vrcholov sa v hernom strome postupuje späť smerom ku koreňovému vrcholu (k počiatočnej pozícii) a ohodnocujú sa ostatné vrcholy stromu. Podľa toho, ktorý hráč je v hernom strome aktuálne na ťahu (záleží, či maximalizuje alebo minimalizuje) každý uzol nadobúda maximálnu alebo minimálnu hodnotu zo svojich priamych “potomkov”. Takto sa postupuje až ku koreňovému vrcholu (ten obsahuje pozíciu, z ktorej hľadáme optimálny ťah), ktorý je potom ohodnotený najlepšou hodnotou, akú hráč môže z danej počiatočnej (koreňovej) pozície dosiahnuť.

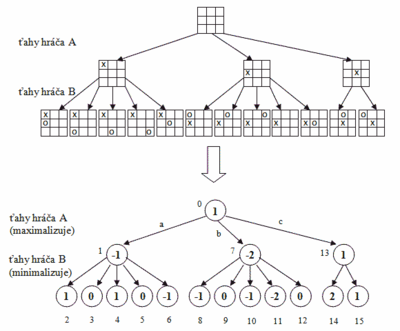
Princíp algoritmu je ukázaný na Obr. 13. Pre väčšiu názornosť v spodnom obrázku nie sú znázornené pozície predstavované jednotlivými vrcholmi. Hĺbka prehľadávania je pre jednoduchosť len 2. Takže celý herný strom je zložený zo všetkých možných polťahov hráča A a následne všetkých možných polťahov hráča B. Strom teda znázorňuje jeden herný ťah. Čísla v jednotlivých vrcholoch predstavujú ohodnotenie danej pozície a čísla pri každom vrchole znázorňujú poradie prechádzania (a vytvárania) vrcholov v hernom strome. Šípky znázorňujú jednotlivé ťahy.

Začína sa z nulovej (koreňovej) pozície a ako prvý je na ťahu hráč A, ktorý podľa dohody maximalizuje (vyberá si také ťahy, ktoré budú mať za následok pozície s čo najvyšším ohodnotením). Vygeneruje sa prvý možný ťah – a hráča A, následkom čoho vznikne pozícia označená číslom 1. Potom sa postupne podľa znázorneného číselného poradia generujú všetky možné ťahy hráča B. Keďže pozície vytvorené následkom ťahov hráča B sú zároveň listovými vrcholmi, tak sa v minimaxovej funkcii ohodnotia. Po vygenerovaní všetkých ťahov hráča B (označených 2 až 6) sa funkcia naspäť vráti k vrcholu č.1 a ohodnotí ho najmenšou (pretože hráč B minimalizuje) hodnotou z hodnôt pozícií patriacich pod vrchol 1. Pridelí sa mu teda hodnota -1. Rovnako sa postupuje aj pre ťahy b a c. Keď už sú ohodnotené všetky vrcholy v druhej úrovni stromu (vrcholy č. 1,7,13), funkcia sa rekurzívne vráti ku koreňovému vrcholu a ohodnotí ho najvyššou (pretože hráč A maximalizuje) hodnotou z vrcholov o jednu úroveň nižších. Zistili sme teda, že z koreňovej pozície (vrchol 0) bude najlepšie urobiť ťah c , ktorý pri najlepšom ťahu hráča B vráti hodnotu 1, ktorá je výhodná pre hráča A. Ak by hráč A urobil na začiatku ťah b, bol by to pre neho najhorší ťah, pretože výsledná pozícia po dvoch polťahoch by mohla mať hodnotu až -2, čo je veľmi výhodné pre hráča B.

Alfa-Beta orezávanie

Obr. 14 – Princíp alfa-beta orezávania

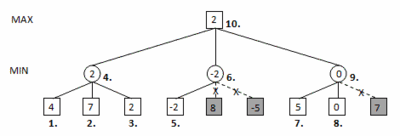
Ide o techniku, ktorej účelom je urýchliť prehľadávanie stromu v metóde minimax. Dosahuje sa to zmenšením počtu vetiev, ktoré musí algoritmus prejsť. Výhodou použitia tejto techniky je, že nemení výslednú hodnotu (koreňovú) hodnotu nájdenú pomocou minimaxovej metódy. Použitie minimaxu s alfa-beta orezávaním teda produkuje rovnaké výsledky ako samotný algoritmus minimax. Názov alfa-beta orézavanie je odvodený od dvoch premenných, ktoré sa v tomto algoritme používajú. Premenná alfa predstavuje minimálne isté skóre maximalizujúceho hráča a beta maximálne isté skóre minimalizujúceho hráča. Inak povedané alfa je maximálna dolná hranica možných ťahov maximalizujúceho hráča a beta minimálna horná hranica možných ťahov minimalizujúceho hráča. Tieto dve premenné udávajú interval hodnôt prehľadávaných pozícií. Princíp algoritmu je zobrazený na obrázku 14.

Prvý je na ťahu maximalizujúci hráč. Po ňom ide minimalizujúci hráč a urobí ťah, ktorý zároveň vedie ku koncovej pozícii hry. Tu sa zmenené pozície hry ohodnotia (podľa poradia pri jednotlivých políčkach). Minimalizujúci hráč potom vyberie ťah, ktorý bude mať za následok pozíciu s čo najmenšou hodnotou. To je hodnota 2, ktorá sa presunie do ohodnotenia pozície o vrstvu vyššie. Maximalizujúci hráč potom urobí druhý svoj možný ťah a následne ťahá minimalizujúci hráč. Znova sa ohodnotí koncová pozícia (políčko č.5), ktorá má hodnotu -2. Je jasné, že minimalizujúci hráč si vyberie pozíciu buď s touto hodnotou (-2) alebo ešte nižšou. Pre maximalizujúceho hráča je však podstatné, aby hodnota bola čo najvyššia a po prvom ťahu by pozícia mala hodnotu 2, čo je lepšie ako -2 (prípadne ešte menej), takže ďalej už ťahy minimalizujúceho hráča skúmať netreba, pretože pre maximalizujúceho hráča je jasné, že jeho druhý ťah je nevýhodný. Rovnaká situácia nastane aj pri treťom možnom ťahu maximalizujúceho hráča, kedy znova minimalizujúci hráč môže urobiť ťah, ktorý bude mať za následok pozíciu s hodnotou menšou ako 2. Preto ani tu netreba uvažovať všetky ťahy minimalizujúceho hráča.