ElectriX: Rozdiel medzi revíziami
d |
|||
| Riadok 9: | Riadok 9: | ||
| Opis || <span itemprop="description">Výuková aplikácia pre výpočet parametrov jednoduchých elektrických obvodov.</span> | | Opis || <span itemprop="description">Výuková aplikácia pre výpočet parametrov jednoduchých elektrických obvodov.</span> | ||
|- | |- | ||
| − | | Použité knižnice || Knižnica [[Meracie komponenty| | + | | Použité knižnice || Knižnica [[Meracie komponenty|info.kiwiki.measurelib]] |
|- | |- | ||
| Ikona || [[Súbor:electrix_ico.png|96px|link=measureDemo]] | | Ikona || [[Súbor:electrix_ico.png|96px|link=measureDemo]] | ||
Aktuálna revízia z 20:34, 25. marec 2013
| Jazyk EN SK | Navigácia | Android projekty -> Meracie komponenty -> ElectriX |
| Názov | ElectriX |
| Verzia | 1 (junior) |
| Opis | Výuková aplikácia pre výpočet parametrov jednoduchých elektrických obvodov. |
| Použité knižnice | Knižnica info.kiwiki.measurelib |
| Ikona | 
|
| Kompatibilita | Minimálna verzia OS Android: 2.2 -FroYo (API 8) |
| Vhodné pre | Tablety, telefóny s uhlopriečkou viac ako 3" |
| Jazyk | Angličtina, Slovenčina (EN, SK) |
| Stiahnutie |  
|
| Autor | Juraj Ďuďák (Redaktor:Juraj) |
Obsah
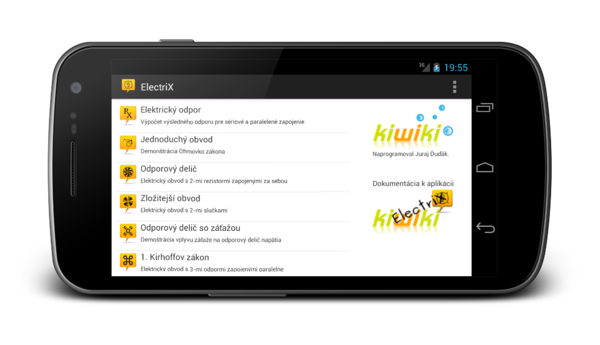
Vlastnosti
- Aplikácia simuluje jednoduché elektrické obvody.
- Obsiahnuté príklady demonštrujú aplikáciu Kirhoffových zákonov.
- V aktuálnej verzii sú k dispozícii nasledovné elektrické obvody:
- Elektrický odpor - Výpočet výsledného odporu pre sériové a paralelené zapojenie
- Jednoduchý obvod - Demonštrácia Ohmovko zákona
- Odporový delič - Elektrický obvod s 2-mi rezistormi zapojenými za sebou
- Zložitejší obvod - Elektrický obvod s 2-mi slučkami
- Odporový delič so záťažou - Demoštrácia vplyvu záťaže na odporový delič napätia
- 1. Kirhoffov zákon - Elektrický obvod s 3-mi odpormi zapojenými paralelne
Hlavná obrazovka aplikácie ElecriX
Ovládanie
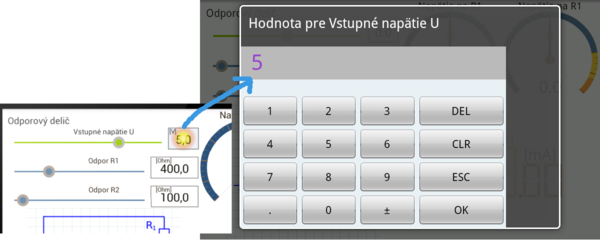
Zmena parametrov pripravených obvodov sa deje prostredníctvom príslušných označených posuvníkov. Po takejto zmene je okamžite prepočítaný celý obvod a hodnoty sledovaných veličín sa zobrazia na pripravených meracích prístrojoch. Pre presné zadanie hodnoty je možnosť využiť softvérovú numerickú klávesnicu, ktorá sa vyvolá kliknutím/tapnutím na časť posubníka, kde je zobrazená jeho hodnota. Tento postup je naznačený na nasledujúcom obrázku.
Analýza riešení elektrických obvodov
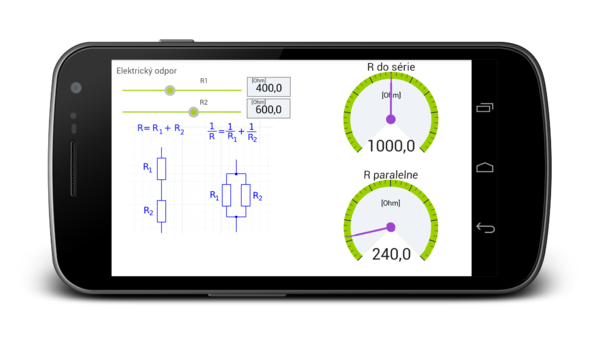
Elektrický odpor
Ukážka výpočtu výsledného elektrického odporu z dvoch rezistorov zapojených do série a paralelne.
Použité vzťahy
- Sériové zapojenie: [math]R = R_1 + R_2[/math]
- Paralelné zapojenie: [math]\frac{1}{R}=\frac{1}{R_1}+\frac{1}{R_2}, R=\frac{R_1R_2}{R_1+R_2}[/math]
Náhľad
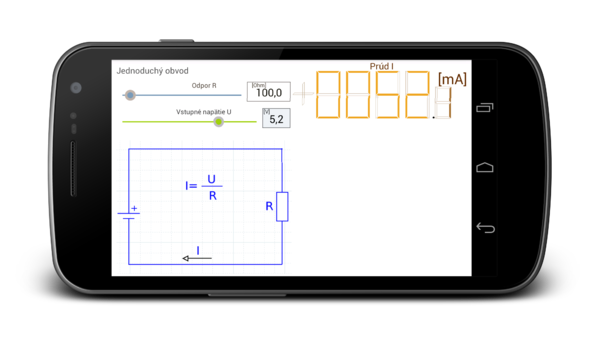
Jednoduchý elektrický obvod
Ukážka výpočtu výsledného elektrického odporu z dvoch rezistorov zapojených do série a paralelne.
Použité vzťahy
- Pre toto zapojenie platí Ohmov zákon: U=R*I
- Pre výpočet prúdu teda platí: I=U/R
Náhľad
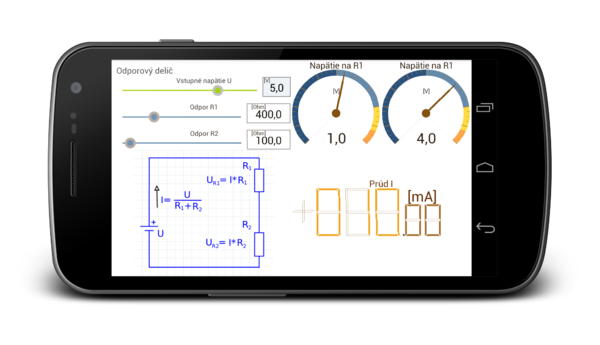
Odporový delič
Jednoduchý elektrický obvod s 2-mi rezistiormi zapojenými za sebou. Na každom odpore je úbytok napätia úmerný vzájomnému pomeru hodnôt rezistorov. Súčet týchto úbytkov je rovný napájaciemu napätiu U.
Použité vzťahy
- Pre toto zapojenie platí Ohmov zákon: U=R*I, kde odpor R je súčtom odporov R1+R2; Platí teda: U=(R1+R2)*I
- Pre úbytok napätia na jednotlivých odporoch platí:
- [math]U(R_1)=I*R_1[/math]
- [math]U(R_2)=I*R_2[/math]
Náhľad
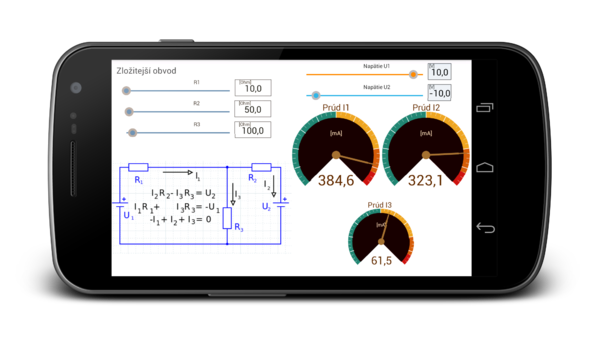
Zložitejší obvod
Elektrický obvod s dvoma slučkami. Pre riešenie tohto obvodu sú použité 1. a 2. Kirhoffov zákon [1].
Použité vzťahy
Označíme si smery elektrického prúdu tak, ako je na nasledujúcom obrázku.
Pre prvú slučku platí rovnica: [math]-U_1 + I_1R_1+ I_3R_3 = 0[/math]. Pre druhú slučku: [math]U_2+I_2R_2-I_3R_3 = 0[/math]. Pre prúdy platí: [math]I_1-I_2-I_3=0[/math]
Rovnice si môžeme prepísať nasledovne:
[math] \begin{matrix} I_1R_1 & & +I_3R_3 & =U_1\\ & I_2R_2 & -I_3R_3 & =U_2\\ I_1 & -I_2 & -I_3 & = 0 \end{matrix} [/math]
V maticovom tvare majú rovnice tvar:
[math] \begin{pmatrix} R_1 & 0 & R_3\\ 0 & R_2 & -R_3\\ 1 & -1 & -1 \end{pmatrix}\cdot \begin{pmatrix} I_1\\ I_2\\ I_3 \end{pmatrix} = \begin{pmatrix} U_1\\ -U_2\\ 0 \end{pmatrix} [/math]
Túto sústavu rovníc môžeme prepísať symbolicky ako:
[math]\mathbf{R}\cdot \mathbf{I}=\mathbf{U}[/math]
potom je riešenie:
[math]\mathbf{I}=\mathbf{R^{-1}}\cdot \mathbf{U}[/math]
kde [math]\mathbf{R^{-1}}[/math] je inverzná matica. Postup pre výpočet inverznej matice je známy [2][3]. Výsledná inverzná matica [math]\mathbf{R^{-1}}[/math] má hodnotu:
[math] \mathbf{R^{-1}}=\begin{pmatrix} -R_2+R_3& -R_3&-R_2R_3 \\ -R_3 & -R_1-R_3 & R_1R_3\\ -R_2 & R_1 & R_1R_2 \end{pmatrix}\cdot \frac{1}{D} [/math]
Kde D je determinant matice:
[math]D = -(R_1*R_2 + R_2*R_3 + R_1*R_3)[/math]
Riešením rovnice je:
[math] \mathbf{I}=\mathbf{R^{-1}}\cdot \mathbf{U} = \frac{1}{D} \begin{pmatrix} -R_2-R_3 & -R_3 & -R_2R_3\\ -R_3 & -R_1-R_3 & R_1R_3\\ -R_2 & R_1 & R_1R_2 \end{pmatrix} \cdot \begin{pmatrix} U_1\\ -U_2\\ 0 \end{pmatrix} = \frac{1}{D} \begin{pmatrix} -U_1(R_2+R_3) + U_2R_3\\ -U_1R_3 - U_2(R_1+R_3)\\ -U_1R_2-U_2R_1 \end{pmatrix} [/math]
Konečné vyjadrenie riešenia:
[math]I_1 = \frac{-U_1(R_3-R_2) + U_2R_3}{D}[/math]
[math]I_2 = \frac{-U_1R_3 + U_2(R_1+R_3) }{D}[/math]
[math]I_3 = \frac{-U_1R_2 + U_2R_1}{D}[/math]
Náhľad
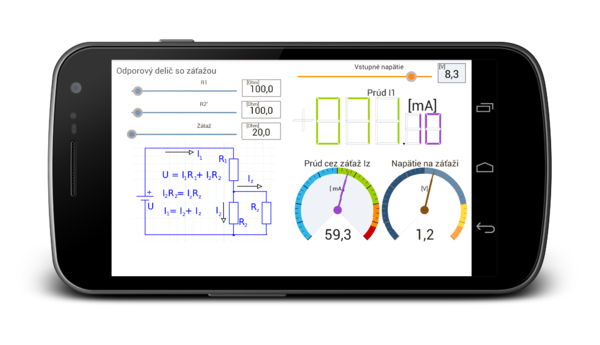
Odporový delič so záťažou
Tento príklad je len špeciálnym prípadom prechádzajúceho príkladu. Rozdiel je v tom, že v druhej vetve nie je zapojený zdroj elektrického napätia. V tomto príklade nás zaujíma úbytok napätia na záťaži (odpor Rz) a prúd prechádzajúci záťažou (Iz).
Použité vzťahy
Sústava rovníc pre tento príklad:
[math] \begin{pmatrix} R_1 & R_2 & 0\\ 0 & R_2 & -R_z\\ 1 & -1 & -1 \end{pmatrix} \cdot \begin{pmatrix} I_1\\ I_2\\ I_z \end{pmatrix}= \begin{pmatrix} U\\ 0\\ 0 \end{pmatrix} [/math]
Inverzná matica R^(-1) je:
[math] \mathbf{R^{-1}}= \begin{pmatrix} R_2+R_z & X & X\\ R_z & X & X\\ R_z & X & X \end{pmatrix} [/math]
X sú prvky matice, ktoré nepotrebujeme počítať, pretože vektor pravej strany rovnice má v druhom a treťom riadku nuly. Výsledné prúdy majú hodnoty:
[math]I_1= \frac{U(R_2+Rz)}{D}[/math]
[math]I_2= \frac{URz}{D}[/math]
[math]I_z= \frac{UR_2}{D}[/math]
kde D je determinant matice R a je rovný:
[math]D=R_1R_2 + R_2R_z + R_1R_z[/math]
Náhľad
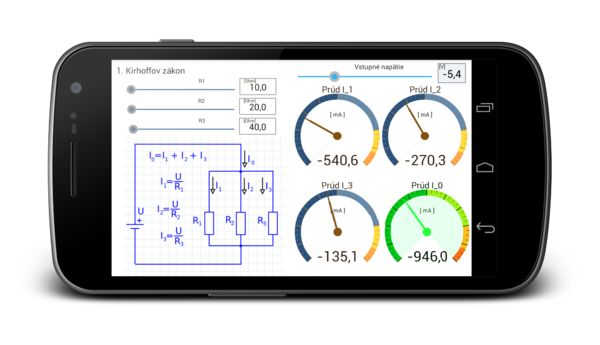
1. Kirhoffov zákon
Nasledujúci príklad demonštruje použitie 1. Kirhoffového zákona. V obvode sú zapojené 3 rezistory v paralelnom zapojení, teda úbytok napätia na týchto rezistoroch je rovnaký. Líšia sa len hodnoty prúdov, ktoré tečú cez tieto vetvy obvodu.
Použité vzťahy
Úbytok napätia na odporoch je totožný s hodnotou napájacieho napätia U. Pre jednotlivé prúdy platia vzťahy:
- [math]I_1 = \frac{U}{R_1}[/math]
- [math]I_2 = \frac{U}{R_2}[/math]
- [math]I_3 = \frac{U}{R_3}[/math]
- Celkový prúd je rovný [math]I = I_1+I_2+I_3[/math]
Náhľad