Analógové spracovanie signálov - filtre: Rozdiel medzi revíziami
| (12 medziľahlých úprav od 3 ďalších používateľov nie je zobrazených) | |||
| Riadok 1: | Riadok 1: | ||
| − | + | [[Kategória:Konfigurovateľné mikroprocesorové systémy]] | |
| − | + | [[Kategória:Analógové spracovanie signálov]] | |
| − | ---- | + | {{sablona_mikroprocoserove_systemy|Analógové spracovanie signálov|Prevodníky ADC|Aproximačné prevodníky|Delta-Sigma prevodníky|Prevodníky DAC|Analógové spracovanie signálov - zosilňovače|Analógové spracovanie signálov - komparátor|Spracovanie prerušenia od komparátora|Analógové spracovanie signálov - filtre|Návrh a realizácia filtrov|Šumy v elektronických systémoch}} |
| − | + | ==Analógové filtre== | |
| − | |||
| − | |||
Analógové filtre sú základným stavebným kameňom pre spracovanie signálu. Majú veľké použitie v elektronike. Medzi ich mnohé aplikácie je oddelenia audio signálu pred aplikáciou do basy, oddelenie viac telefónnych hovorov v jedenom kanály, výber zvolenej rozhlasovej stanice v rozhlasovom prijímači a odmietnutie druhých. Pasívne lineárne elektronické analógové filtre možno opísať lineárnymi diferenciálnymi rovnicami. Filtre sú zložené z kondenzátorov, tlmiviek a odporov. Sú navrhnuté na plynulú reguláciu analógového signálu. Analógové filtre sú najčastejšie používané v aplikáciách, kde je potrebné zosilniť určitú frekvenciu a zamietnúť inú z analógového signálu. Analógové filtre hrali dôležitú úlohu vo vývoji elektroniky. Najmä v oblasti telekomunikácií. Filtre mali zásadný význam v technologickom pokroku a boli zdrojom obrovských ziskov pre telekomunikačné spoločnosti. Dnes má často prednosť vykonávať filtrovanie v digitálnej oblasti, kde sa ľahšie plnia zložité algoritmy, ale analógové filtre stále nachádzajú uplatnenie najmä pri jednoduchých úlohách. Pri vyšších frekvenciách je digitálna technológia stále nepraktická, alebo aspoň, menej efektívna z hľadiska nákladov. Je možné navrhnúť lineárne analógové mechanické filtre pomocou mechanických súčastí, ktoré filtrujú mechanickými vibráciami alebo akustickými vĺnami. V skutočnosti niektoré z prvých nápadov pre filtre boli akustické rezonátory, pretože technológia elektroniky bola zle chápaná v tej dobe. V zásade možno design týchto filtrov dosiahnuť výhradne v oblasti elektronických náprotivkov mechanických veličín. | Analógové filtre sú základným stavebným kameňom pre spracovanie signálu. Majú veľké použitie v elektronike. Medzi ich mnohé aplikácie je oddelenia audio signálu pred aplikáciou do basy, oddelenie viac telefónnych hovorov v jedenom kanály, výber zvolenej rozhlasovej stanice v rozhlasovom prijímači a odmietnutie druhých. Pasívne lineárne elektronické analógové filtre možno opísať lineárnymi diferenciálnymi rovnicami. Filtre sú zložené z kondenzátorov, tlmiviek a odporov. Sú navrhnuté na plynulú reguláciu analógového signálu. Analógové filtre sú najčastejšie používané v aplikáciách, kde je potrebné zosilniť určitú frekvenciu a zamietnúť inú z analógového signálu. Analógové filtre hrali dôležitú úlohu vo vývoji elektroniky. Najmä v oblasti telekomunikácií. Filtre mali zásadný význam v technologickom pokroku a boli zdrojom obrovských ziskov pre telekomunikačné spoločnosti. Dnes má často prednosť vykonávať filtrovanie v digitálnej oblasti, kde sa ľahšie plnia zložité algoritmy, ale analógové filtre stále nachádzajú uplatnenie najmä pri jednoduchých úlohách. Pri vyšších frekvenciách je digitálna technológia stále nepraktická, alebo aspoň, menej efektívna z hľadiska nákladov. Je možné navrhnúť lineárne analógové mechanické filtre pomocou mechanických súčastí, ktoré filtrujú mechanickými vibráciami alebo akustickými vĺnami. V skutočnosti niektoré z prvých nápadov pre filtre boli akustické rezonátory, pretože technológia elektroniky bola zle chápaná v tej dobe. V zásade možno design týchto filtrov dosiahnuť výhradne v oblasti elektronických náprotivkov mechanických veličín. | ||
| − | + | ==Historický vývoj== | |
| − | Existujú tri hlavné fázy v histórii vývoja pasívnych analógových filtrov: | + | Existujú tri hlavné fázy v histórii vývoja pasívnych analógových filtrov:<br> 1. Jednoduché filtre. Frekvenčné závislosti pre kondenzátory a cievky boli známe veľmi skoro. Rezonančný jav bol tiež známy veľmi skoro a bolo možné vyrábať jednoduché filtre s týmito komponentmi. Aj keď pokusy boli vykonané v roku 1880 pri uplatnení na telegraf, tieto návrhy sa ukázali ako nedostatočné.<br> 2. Grafické filtre. Grafický filter vznikol z teórie prenosovej linky. Prvýkrát boli filtre vyrobené tak, že mali presne kontrolovateľné pásmo priepusti a ďalšie parametre. Tento vývoj bol v roku 1920 ale filtre vyrobené na tento spôsob boli širšie použité až v roku 1980. Dnes klesá použitie týchto filtrov, pretože sa znížilo používanie analógových telekomunikačných zariadení. Ich použitie malo hospodársky veľký význam pre použitie na medzimestské a medzinárodné telefónne linky. <br> 3. Syntéza sieťových filtrov. Matematické základy boli položené v rokoch 1930 a 1940. Po skončení druhej svetovej vojny sa stali primárnym nástrojom filtrov. Podstatou je, že vytvára dizajn, ktorý bude (aspoň pokiaľ by boli použité ideálne komponenty) presne reprodukovať odpovede pôvodne uvedených v čiernej skrinke. <br> |
<font size = "4">'''Návrh filtrov'''</font> | <font size = "4">'''Návrh filtrov'''</font> | ||
| Riadok 22: | Riadok 20: | ||
* Linkwitz-Rileyov filter | * Linkwitz-Rileyov filter | ||
| − | + | ==Butterworthov filter== | |
Butterworth bol známy riešením matematických problémov, ktoré boli považované za nemožné. Jeho práca ďaleko predbehla svoju dobu a filter nebol v spoločnom užívaní viac ako 30 rokov po jeho uverejnení. V tej dobe filtre boli z veľkej časti určené metódou pokus, omyl, pre ich matematickú zložitosť. Butterworth uvádza cieľ svojej práce: "Ideálny elektrický filter by mal nielen úplne odmietnuť nežiaduce kmitočty, ale mal by tiež mať jednotnú citlivosť pre potrebnú frekvenciu." V čase, keď frekvenčné charakteristiky filtrov obsahovali značné množstvo zvlnenia v priepustnom pásme a výber komponentov nebol dobrý Butterworth ukázal, že pre nízke prepuste by mohlo byť filter navrhnutý tak aby jeho frekvenčná charakteristika bola | Butterworth bol známy riešením matematických problémov, ktoré boli považované za nemožné. Jeho práca ďaleko predbehla svoju dobu a filter nebol v spoločnom užívaní viac ako 30 rokov po jeho uverejnení. V tej dobe filtre boli z veľkej časti určené metódou pokus, omyl, pre ich matematickú zložitosť. Butterworth uvádza cieľ svojej práce: "Ideálny elektrický filter by mal nielen úplne odmietnuť nežiaduce kmitočty, ale mal by tiež mať jednotnú citlivosť pre potrebnú frekvenciu." V čase, keď frekvenčné charakteristiky filtrov obsahovali značné množstvo zvlnenia v priepustnom pásme a výber komponentov nebol dobrý Butterworth ukázal, že pre nízke prepuste by mohlo byť filter navrhnutý tak aby jeho frekvenčná charakteristika bola | ||
| − | + | <math>G=\sqrt{\frac{1}{1+{{\omega }^{2n}}}}</math> | |
kde ω je uhlová frekvencia v radiánoch za sekundu, n je počet reaktívnych prvkov vo filtri. Butterworth sa zaoberal vo svojej práci iba filtrami s párnym počtom pólov. Jeho odozva frekvencií 2, 4, 6, 8, a 10 a pole filtrov je zobrazená ako A, B, C, D, E na obrázku. | kde ω je uhlová frekvencia v radiánoch za sekundu, n je počet reaktívnych prvkov vo filtri. Butterworth sa zaoberal vo svojej práci iba filtrami s párnym počtom pólov. Jeho odozva frekvencií 2, 4, 6, 8, a 10 a pole filtrov je zobrazená ako A, B, C, D, E na obrázku. | ||
| Riadok 34: | Riadok 32: | ||
| align="center" width=500 | [[Súbor:Analógové_filtre_01.jpg ]] | | align="center" width=500 | [[Súbor:Analógové_filtre_01.jpg ]] | ||
|- | |- | ||
| − | | align="center" width=500 | | + | | align="center" width=500 | Frekvenčná odozva z pôvodnej práce Butterwortha |
|} | |} | ||
</center> | </center> | ||
| Riadok 40: | Riadok 38: | ||
Butterworth vyriešiť rovnice pre dva a štyri prúty filtra a ukázal, ako by mohol byť odstupňovaný elektronkovým zosilňovačom. Butterworth zistil, že to bolo možné nastaviť zložkou hodnoty filtra na kompenzáciu odporu vinutia z tlmivky. Butterworth tiež ukázal, že jeho základný filter môže byť upravený na nízku priepusť, vysokú priepusť, band-pass, a band-stop verzie. On zistil, že tento typ filtra by mohol byť vytvorený s nepárnym počtom pólov. Butterworthov filter je jeden typ filtra pre spracovanie signálu. Je navrhnutý tak, aby frekvenčná odozva bola plochá priepustného pásma. Frekvenčná charakteristika filtra Butterwortha je maximálne plochá (nemá vlnky) v priepustnom pásme. | Butterworth vyriešiť rovnice pre dva a štyri prúty filtra a ukázal, ako by mohol byť odstupňovaný elektronkovým zosilňovačom. Butterworth zistil, že to bolo možné nastaviť zložkou hodnoty filtra na kompenzáciu odporu vinutia z tlmivky. Butterworth tiež ukázal, že jeho základný filter môže byť upravený na nízku priepusť, vysokú priepusť, band-pass, a band-stop verzie. On zistil, že tento typ filtra by mohol byť vytvorený s nepárnym počtom pólov. Butterworthov filter je jeden typ filtra pre spracovanie signálu. Je navrhnutý tak, aby frekvenčná odozva bola plochá priepustného pásma. Frekvenčná charakteristika filtra Butterwortha je maximálne plochá (nemá vlnky) v priepustnom pásme. | ||
| − | + | ==Prenosová funkcia== | |
Ako všetky filtre, typický prototyp je filter nízka priepusť, ktorý môže byť upravený do vysokej priepuste, alebo umiestnený v sérii s ostatnými a tvoriť band-pass a band-stop filtre.<br>Zisk G (ω) na n-tú nízka priepusť: | Ako všetky filtre, typický prototyp je filter nízka priepusť, ktorý môže byť upravený do vysokej priepuste, alebo umiestnený v sérii s ostatnými a tvoriť band-pass a band-stop filtre.<br>Zisk G (ω) na n-tú nízka priepusť: | ||
| − | + | ||
| + | <math>{{G}^{2}}(\omega )=|H(j\omega ){{|}^{2}}=\frac{G_{0}^{2}}{1+{{(\frac{\omega }{{{\omega }_{c}}})}^{2n}}}</math> | ||
| + | |||
kde<br> n = požiadavka na filter<br> Ωc = medzná frekvencia (približne 3dB)<br> G0 je zisk nuly frekvencie<br><br>Je vidieť, že ako n sa blíži k nekonečnu, zisk sa stáva obdĺžnik funkcie a frekvencie pod ωc bude odovzdaný s G0, zatiaľ čo frekvencie nad ωc budú zrušené. Pre menšie hodnoty n, bude menej ostré viď obrázok. | kde<br> n = požiadavka na filter<br> Ωc = medzná frekvencia (približne 3dB)<br> G0 je zisk nuly frekvencie<br><br>Je vidieť, že ako n sa blíži k nekonečnu, zisk sa stáva obdĺžnik funkcie a frekvencie pod ωc bude odovzdaný s G0, zatiaľ čo frekvencie nad ωc budú zrušené. Pre menšie hodnoty n, bude menej ostré viď obrázok. | ||
| Riadok 52: | Riadok 52: | ||
| align="center" width=500 | [[Súbor:Analógové_filtre_02.png ]] | | align="center" width=500 | [[Súbor:Analógové_filtre_02.png ]] | ||
|- | |- | ||
| − | | align="center" width=500 | | + | | align="center" width=500 | Filter dolná priepusť |
|} | |} | ||
</center> | </center> | ||
| − | + | ==Realizácia Filtrov== | |
Existuje celý rad rôznych topológií pre realizáciu lineárneho analógového filtra. Najčastejšie používaná topológia pre pasívnu realizáciu je Cauer a najčastejšie používaná topológia pre aktívnu realizáciu je Sallen-Key topológia. | Existuje celý rad rôznych topológií pre realizáciu lineárneho analógového filtra. Najčastejšie používaná topológia pre pasívnu realizáciu je Cauer a najčastejšie používaná topológia pre aktívnu realizáciu je Sallen-Key topológia. | ||
| Riadok 64: | Riadok 64: | ||
Topológia Cauer využíva pasívne prvky (kondenzátory a sériu induktorov) na vytvorenie lineárneho analógového filtra. Butterworthov filter s danou prenosovou funkciou môže byť realizovaný pomocou 1-formy topológie Cauer. K-ty element je daný vzťahom: | Topológia Cauer využíva pasívne prvky (kondenzátory a sériu induktorov) na vytvorenie lineárneho analógového filtra. Butterworthov filter s danou prenosovou funkciou môže byť realizovaný pomocou 1-formy topológie Cauer. K-ty element je daný vzťahom: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <math>{{C}_{k}}=2\sin [\frac{(2k-1)}{2n}\pi ]</math> k= nepárne | |
| − | + | ||
| − | + | <math>{{L}_{k}}=2\sin [\frac{(2k-1)}{2n}\pi ]</math> k= párne | |
| − | + | ||
| − | |||
Filter sa môže začať so sériou cievok, v takom prípade L<sub>k</sub> je k nepárne a C<sub>k</sub> je k párne. | Filter sa môže začať so sériou cievok, v takom prípade L<sub>k</sub> je k nepárne a C<sub>k</sub> je k párne. | ||
| Riadok 82: | Riadok 77: | ||
| align="center" width=500 | [[Súbor:Analógové_filtre_03.png ]] | | align="center" width=500 | [[Súbor:Analógové_filtre_03.png ]] | ||
|- | |- | ||
| − | | align="center" width=500 | | + | | align="center" width=500 | Topológia Cauer |
|} | |} | ||
</center> | </center> | ||
| Riadok 93: | Riadok 88: | ||
| align="center" width=500 | [[Súbor:Analógové_filtre_04.png ]] | | align="center" width=500 | [[Súbor:Analógové_filtre_04.png ]] | ||
|- | |- | ||
| − | | align="center" width=500 | | + | | align="center" width=500 | Topológia Sallen-Key |
|} | |} | ||
</center> | </center> | ||
| Riadok 99: | Riadok 94: | ||
prenosová funkcia | prenosová funkcia | ||
| − | H(s)= | + | <math>H\left( s \right)=\frac{{{V}_{out}}(s)}{{{V}_{in}}\left( s \right)}=\frac{1}{1+{{C}_{2}}\left( {{R}_{1}}+{{R}_{2}} \right)s+{{C}_{1}}{{C}_{2}}{{R}_{1}}{{R}_{2}}{{s}^{2}}}</math> |
Chceme aby menovateľ bol jedným z kvadratických polynómov Butterwortha. Za predpokladu, že ωc = 1, bude platiť: | Chceme aby menovateľ bol jedným z kvadratických polynómov Butterwortha. Za predpokladu, že ωc = 1, bude platiť: | ||
| − | + | ||
| + | |||
| + | <math>{{C}_{1}}{{C}_{2}}{{R}_{1}}{{R}_{2}}=1\,\!</math> | ||
| + | |||
| + | |||
a | a | ||
| − | + | ||
| + | <math>{{C}_{2}}\left( {{R}_{1}}+{{R}_{2}} \right)=-2\cos \cos \left( \frac{2k+n-1}{2n}\pi \right)</math> | ||
| + | |||
Zostávajú dve zložky nedefinované, ktoré môžu byť zvolené podľa želania. | Zostávajú dve zložky nedefinované, ktoré môžu byť zvolené podľa želania. | ||
| Riadok 115: | Riadok 116: | ||
| align="center" width=500 | [[Súbor:Analógové_filtre_05.png ]] | | align="center" width=500 | [[Súbor:Analógové_filtre_05.png ]] | ||
|- | |- | ||
| − | | align="center" width=500 | | + | | align="center" width=500 | Porovnanie filtrov |
|} | |} | ||
</center> | </center> | ||
| Riadok 121: | Riadok 122: | ||
Butterworthov filter je pomalší okolo medznej frekvencie ale zato nevznikajú zvlnenia. | Butterworthov filter je pomalší okolo medznej frekvencie ale zato nevznikajú zvlnenia. | ||
| − | + | == Odkazy a literatúra == | |
| + | # http://en.wikipedia.org/wiki/Analog_filter | ||
| + | # http://en.wikipedia.org/wiki/Butterworth_filter | ||
Aktuálna revízia z 09:10, 21. marec 2013
| Predmet |
|
|---|---|
| Konfigurovateľné mikroprocesorové systémy | |
| Tématická časť: | |
| Analógové spracovanie signálov |
Obsah
Analógové filtre
Analógové filtre sú základným stavebným kameňom pre spracovanie signálu. Majú veľké použitie v elektronike. Medzi ich mnohé aplikácie je oddelenia audio signálu pred aplikáciou do basy, oddelenie viac telefónnych hovorov v jedenom kanály, výber zvolenej rozhlasovej stanice v rozhlasovom prijímači a odmietnutie druhých. Pasívne lineárne elektronické analógové filtre možno opísať lineárnymi diferenciálnymi rovnicami. Filtre sú zložené z kondenzátorov, tlmiviek a odporov. Sú navrhnuté na plynulú reguláciu analógového signálu. Analógové filtre sú najčastejšie používané v aplikáciách, kde je potrebné zosilniť určitú frekvenciu a zamietnúť inú z analógového signálu. Analógové filtre hrali dôležitú úlohu vo vývoji elektroniky. Najmä v oblasti telekomunikácií. Filtre mali zásadný význam v technologickom pokroku a boli zdrojom obrovských ziskov pre telekomunikačné spoločnosti. Dnes má často prednosť vykonávať filtrovanie v digitálnej oblasti, kde sa ľahšie plnia zložité algoritmy, ale analógové filtre stále nachádzajú uplatnenie najmä pri jednoduchých úlohách. Pri vyšších frekvenciách je digitálna technológia stále nepraktická, alebo aspoň, menej efektívna z hľadiska nákladov. Je možné navrhnúť lineárne analógové mechanické filtre pomocou mechanických súčastí, ktoré filtrujú mechanickými vibráciami alebo akustickými vĺnami. V skutočnosti niektoré z prvých nápadov pre filtre boli akustické rezonátory, pretože technológia elektroniky bola zle chápaná v tej dobe. V zásade možno design týchto filtrov dosiahnuť výhradne v oblasti elektronických náprotivkov mechanických veličín.
Historický vývoj
Existujú tri hlavné fázy v histórii vývoja pasívnych analógových filtrov:
1. Jednoduché filtre. Frekvenčné závislosti pre kondenzátory a cievky boli známe veľmi skoro. Rezonančný jav bol tiež známy veľmi skoro a bolo možné vyrábať jednoduché filtre s týmito komponentmi. Aj keď pokusy boli vykonané v roku 1880 pri uplatnení na telegraf, tieto návrhy sa ukázali ako nedostatočné.
2. Grafické filtre. Grafický filter vznikol z teórie prenosovej linky. Prvýkrát boli filtre vyrobené tak, že mali presne kontrolovateľné pásmo priepusti a ďalšie parametre. Tento vývoj bol v roku 1920 ale filtre vyrobené na tento spôsob boli širšie použité až v roku 1980. Dnes klesá použitie týchto filtrov, pretože sa znížilo používanie analógových telekomunikačných zariadení. Ich použitie malo hospodársky veľký význam pre použitie na medzimestské a medzinárodné telefónne linky.
3. Syntéza sieťových filtrov. Matematické základy boli položené v rokoch 1930 a 1940. Po skončení druhej svetovej vojny sa stali primárnym nástrojom filtrov. Podstatou je, že vytvára dizajn, ktorý bude (aspoň pokiaľ by boli použité ideálne komponenty) presne reprodukovať odpovede pôvodne uvedených v čiernej skrinke.
Návrh filtrov
Podstatou je začať z požadovanej odozvy filtra vytvárať sieť, ktorá zabezpečuje, že odpoveď sa blíži k v stanoveným hraniciam. Inverzný model začína s danou sieťou a za použitia rôznych elektrických obvodov predpovedá odozvy siete. Výhodou je, že poskytuje riešenia, ktoré presne spĺňajú špecifikáciu návrhu. To nie je prípad s grafickými filtrami, kde je potrebné pre ich návrh miera skúseností. Sieť na druhej strane, sa stará o ukončenie impedanciou jednoducho tým, že ich začlenenie je do navrhnutej siete. Typy filtrov:
- Butterworthov filter
- Chebyshevov filter
- Eliptický filter
- Besselov filter
- Gaussianov filter
- Optimum "L" filter
- Linkwitz-Rileyov filter
Butterworthov filter
Butterworth bol známy riešením matematických problémov, ktoré boli považované za nemožné. Jeho práca ďaleko predbehla svoju dobu a filter nebol v spoločnom užívaní viac ako 30 rokov po jeho uverejnení. V tej dobe filtre boli z veľkej časti určené metódou pokus, omyl, pre ich matematickú zložitosť. Butterworth uvádza cieľ svojej práce: "Ideálny elektrický filter by mal nielen úplne odmietnuť nežiaduce kmitočty, ale mal by tiež mať jednotnú citlivosť pre potrebnú frekvenciu." V čase, keď frekvenčné charakteristiky filtrov obsahovali značné množstvo zvlnenia v priepustnom pásme a výber komponentov nebol dobrý Butterworth ukázal, že pre nízke prepuste by mohlo byť filter navrhnutý tak aby jeho frekvenčná charakteristika bola
[math]G=\sqrt{\frac{1}{1+{{\omega }^{2n}}}}[/math]
kde ω je uhlová frekvencia v radiánoch za sekundu, n je počet reaktívnych prvkov vo filtri. Butterworth sa zaoberal vo svojej práci iba filtrami s párnym počtom pólov. Jeho odozva frekvencií 2, 4, 6, 8, a 10 a pole filtrov je zobrazená ako A, B, C, D, E na obrázku.
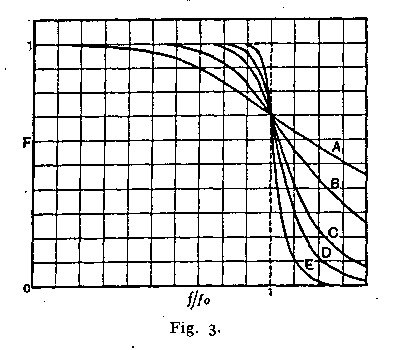
|
| Frekvenčná odozva z pôvodnej práce Butterwortha |
Butterworth vyriešiť rovnice pre dva a štyri prúty filtra a ukázal, ako by mohol byť odstupňovaný elektronkovým zosilňovačom. Butterworth zistil, že to bolo možné nastaviť zložkou hodnoty filtra na kompenzáciu odporu vinutia z tlmivky. Butterworth tiež ukázal, že jeho základný filter môže byť upravený na nízku priepusť, vysokú priepusť, band-pass, a band-stop verzie. On zistil, že tento typ filtra by mohol byť vytvorený s nepárnym počtom pólov. Butterworthov filter je jeden typ filtra pre spracovanie signálu. Je navrhnutý tak, aby frekvenčná odozva bola plochá priepustného pásma. Frekvenčná charakteristika filtra Butterwortha je maximálne plochá (nemá vlnky) v priepustnom pásme.
Prenosová funkcia
Ako všetky filtre, typický prototyp je filter nízka priepusť, ktorý môže byť upravený do vysokej priepuste, alebo umiestnený v sérii s ostatnými a tvoriť band-pass a band-stop filtre.
Zisk G (ω) na n-tú nízka priepusť:
[math]{{G}^{2}}(\omega )=|H(j\omega ){{|}^{2}}=\frac{G_{0}^{2}}{1+{{(\frac{\omega }{{{\omega }_{c}}})}^{2n}}}[/math]
kde
n = požiadavka na filter
Ωc = medzná frekvencia (približne 3dB)
G0 je zisk nuly frekvencie
Je vidieť, že ako n sa blíži k nekonečnu, zisk sa stáva obdĺžnik funkcie a frekvencie pod ωc bude odovzdaný s G0, zatiaľ čo frekvencie nad ωc budú zrušené. Pre menšie hodnoty n, bude menej ostré viď obrázok.
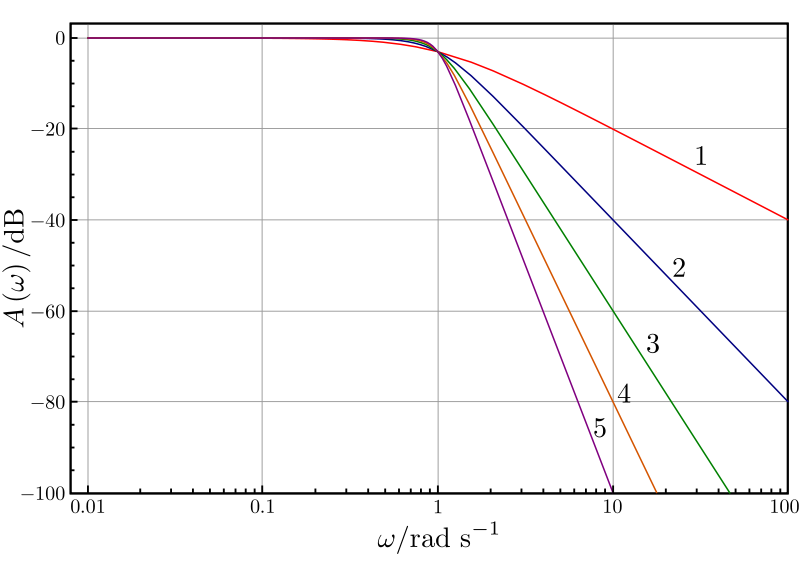
|
| Filter dolná priepusť |
Realizácia Filtrov
Existuje celý rad rôznych topológií pre realizáciu lineárneho analógového filtra. Najčastejšie používaná topológia pre pasívnu realizáciu je Cauer a najčastejšie používaná topológia pre aktívnu realizáciu je Sallen-Key topológia.
Topológia Cauer
Topológia Cauer využíva pasívne prvky (kondenzátory a sériu induktorov) na vytvorenie lineárneho analógového filtra. Butterworthov filter s danou prenosovou funkciou môže byť realizovaný pomocou 1-formy topológie Cauer. K-ty element je daný vzťahom:
[math]{{C}_{k}}=2\sin [\frac{(2k-1)}{2n}\pi ][/math] k= nepárne
[math]{{L}_{k}}=2\sin [\frac{(2k-1)}{2n}\pi ][/math] k= párne
Filter sa môže začať so sériou cievok, v takom prípade Lk je k nepárne a Ck je k párne.
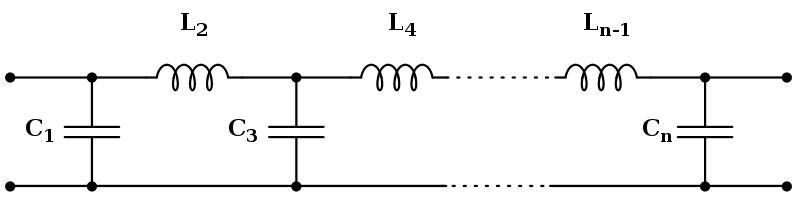
|
| Topológia Cauer |
Topológia Sallen-Key
Sallen-Key topológia používa na vytvorenie lineárneho analógového filtra aktívne a pasívne prvky (väčšinou operačný zosilňovač, odpory a kondenzátory). Vo všeobecnosti je filter vykonávaný kaskádne vo všetkých úrovniach v sérii. Ak existuje reálny pól (v prípade,že n je nepárne), musí to byť vykonávané oddelene, zvyčajne ako RC obvod, a kaskádne s aktívnou úrovňou.
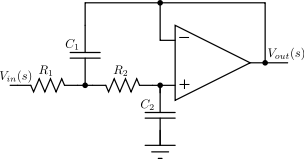
|
| Topológia Sallen-Key |
prenosová funkcia
[math]H\left( s \right)=\frac{{{V}_{out}}(s)}{{{V}_{in}}\left( s \right)}=\frac{1}{1+{{C}_{2}}\left( {{R}_{1}}+{{R}_{2}} \right)s+{{C}_{1}}{{C}_{2}}{{R}_{1}}{{R}_{2}}{{s}^{2}}}[/math]
Chceme aby menovateľ bol jedným z kvadratických polynómov Butterwortha. Za predpokladu, že ωc = 1, bude platiť:
[math]{{C}_{1}}{{C}_{2}}{{R}_{1}}{{R}_{2}}=1\,\![/math]
a
[math]{{C}_{2}}\left( {{R}_{1}}+{{R}_{2}} \right)=-2\cos \cos \left( \frac{2k+n-1}{2n}\pi \right)[/math]
Zostávajú dve zložky nedefinované, ktoré môžu byť zvolené podľa želania.
Porovnanie s inými lineárnymi filtrami
Na obrázku je porovnanie Butterworthovho filtra s Chebyshevovým a eliptickým filtrom.
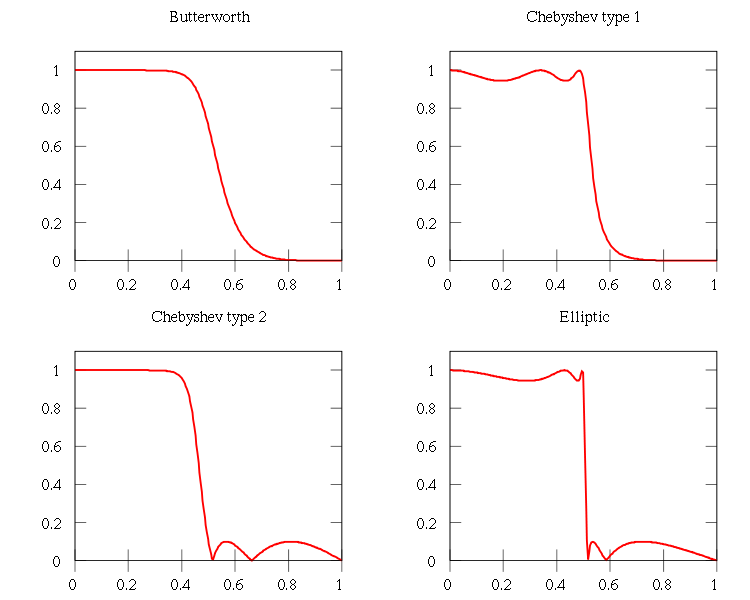
|
| Porovnanie filtrov |
Butterworthov filter je pomalší okolo medznej frekvencie ale zato nevznikajú zvlnenia.