Preladiteľný generátor harmonických kmitov: Rozdiel medzi revíziami
Skočit na navigaci
Skočit na vyhledávání
d |
|||
| (Jedna medziľahlá úprava od jedného ďalšieho používateľa nie je zobrazená) | |||
| Riadok 1: | Riadok 1: | ||
__NOTOC__ | __NOTOC__ | ||
[[Category:Simulácie a modelovanie]] | [[Category:Simulácie a modelovanie]] | ||
| + | {{Simulacia_modelovanie_3|6}} | ||
Príklad demonštruje simuláciu všobecnej diferenciálnej rovnice oscilátora<ref>http://en.wikipedia.org/wiki/Harmonic_oscillator</ref>. Zmenou vstupného parametra simulácie je možné meniť | Príklad demonštruje simuláciu všobecnej diferenciálnej rovnice oscilátora<ref>http://en.wikipedia.org/wiki/Harmonic_oscillator</ref>. Zmenou vstupného parametra simulácie je možné meniť | ||
frekvenciu kmitov oscilátora. Diferenciálna rovnica všeobecného oscilátora má tvar | frekvenciu kmitov oscilátora. Diferenciálna rovnica všeobecného oscilátora má tvar | ||
| − | <math> | + | :<math> |
\frac{d^2 x}{d t^2} = -\omega^2 y_1 | \frac{d^2 x}{d t^2} = -\omega^2 y_1 | ||
</math> | </math> | ||
| Riadok 11: | Riadok 12: | ||
prvého rádu | prvého rádu | ||
| − | <math> | + | :<math> |
y_2 = \frac{1}{\omega} \frac{d y_1}{dt} | y_2 = \frac{1}{\omega} \frac{d y_1}{dt} | ||
</math> | </math> | ||
| − | <math> | + | :<math> |
\frac {d y_2}{dt} = -\omega y_1 | \frac {d y_2}{dt} = -\omega y_1 | ||
</math> | </math> | ||
| Riadok 21: | Riadok 22: | ||
Pre simulačný model je vhodnejšie previesť sústavu rovníc do integrálneho tvaru | Pre simulačný model je vhodnejšie previesť sústavu rovníc do integrálneho tvaru | ||
| − | <math> | + | :<math> |
y_2 = -\omega \int y_1 dt | y_2 = -\omega \int y_1 dt | ||
</math> | </math> | ||
| − | <math> | + | :<math> |
y_1 = \omega \int y_2 dt | y_1 = \omega \int y_2 dt | ||
</math> | </math> | ||
| Riadok 35: | Riadok 36: | ||
| align="center" | [[Súbor:img_var_osc.png | 500px ]] | | align="center" | [[Súbor:img_var_osc.png | 500px ]] | ||
|- | |- | ||
| − | | align="center" width=500 | '''Simulačný model | + | | align="center" width=500 | '''Simulačný model''' |
|} | |} | ||
</center> | </center> | ||
Aktuálna revízia z 21:59, 22. marec 2013
Príklad demonštruje simuláciu všobecnej diferenciálnej rovnice oscilátora[1]. Zmenou vstupného parametra simulácie je možné meniť frekvenciu kmitov oscilátora. Diferenciálna rovnica všeobecného oscilátora má tvar
- [math] \frac{d^2 x}{d t^2} = -\omega^2 y_1 [/math]
Substitúciou prevedieme diferenciálnu rovnicu druhého rádu na dve diferenciálne rovnice prvého rádu
- [math] y_2 = \frac{1}{\omega} \frac{d y_1}{dt} [/math]
- [math] \frac {d y_2}{dt} = -\omega y_1 [/math]
Pre simulačný model je vhodnejšie previesť sústavu rovníc do integrálneho tvaru
- [math] y_2 = -\omega \int y_1 dt [/math]
- [math] y_1 = \omega \int y_2 dt [/math]
Simulačný model pre gsim získame priamym prevodom zápisu diferenciálnych rovníc do grafickej podoby.
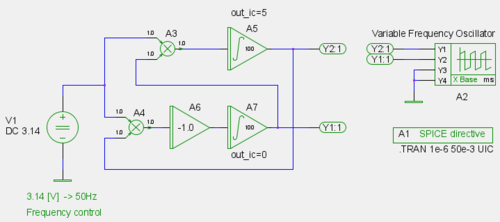
|
| Simulačný model |
Pre korektný štart oscilátora je potrebné definovať počiatočnú podmienku integrátora A5 ako out_ic=5 [V]. Frekvencia kmitov oscilátora je určená hodnotou zdroja V1.
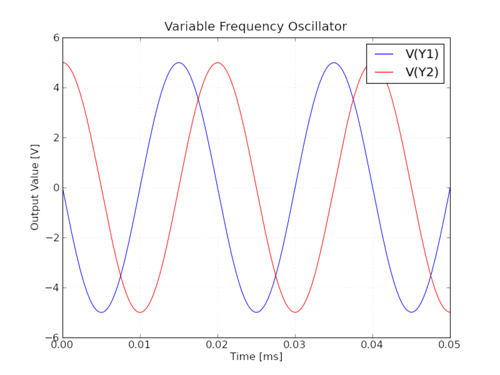
|
| Výsledok simulácie |
Úlohy
- Odvodte výraz pre frekvenciu oscilátora v závislosti od napätia V1.
- Pri akej hodnote V1 bude frekvencia oscilátora rovná 60Hz ?