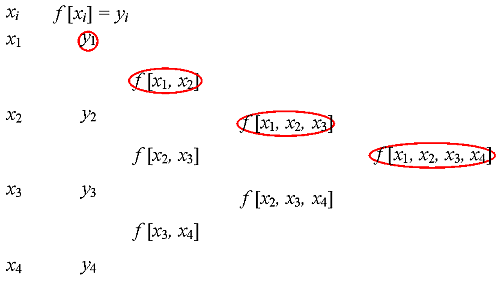Algoritmy numerickej interpolácie (riešené príklady): Rozdiel medzi revíziami
| Riadok 7: | Riadok 7: | ||
==Zadanie== | ==Zadanie== | ||
Riešte problém interpolácie dát. K dispozícii máme n bodov v priestore (x,y). Overte tvrdenie, že existuje len jeden interpolačný polynóm najnižšieho stupňa (''n-1'') pre ''n'' bodov v rovine. Inak povedané, overte že Lagrangeov a Newtonov interpolačný polynóm sú len 2 rôzne zápisy pre jediný polynóm. | Riešte problém interpolácie dát. K dispozícii máme n bodov v priestore (x,y). Overte tvrdenie, že existuje len jeden interpolačný polynóm najnižšieho stupňa (''n-1'') pre ''n'' bodov v rovine. Inak povedané, overte že Lagrangeov a Newtonov interpolačný polynóm sú len 2 rôzne zápisy pre jediný polynóm. | ||
| + | |||
| + | ==Analýza== | ||
| + | Interpolačný polynóm v Lagrangeovom a Newtonovom tvare sú opísané v kapitole [[Algoritmy interpolácie]]. | ||
| + | ===Lagrangeov tvar interpolačného polynómu=== | ||
| + | |||
| + | :<math>L(x) := \sum_{j=0}^{n} y_j \ell_j(x)</math> | ||
| + | :<math>\ell_j(x) := \prod_{i=0,\, i\neq j}^{n} \frac{x-x_i}{x_j-x_i} = \frac{(x-x_0)}{(x_j-x_0)} \cdots \frac{(x-x_{j-1})}{(x_j-x_{j-1})} \frac{(x-x_{j+1})}{(x_j-x_{j+1})} \cdots \frac{(x-x_{n})}{(x_j-x_{n})}.</math> | ||
| + | |||
| + | Postup pri implementácii algoritmu: | ||
| + | |||
| + | Pri výpočte lagrangeovho interpolačného polynómu musíme začať pri výpočte lagrangeových bázových polynómov <math>\ell_j(x)</math>. Ich výpočet je jednoduchý. Označme si <math>\ell_j(x)</math> ako ''lag''. Vstupné údaje sú v poli štruktúr (''data'') typu Bod o veľkosti ''n''. | ||
| + | <source lang="c"> | ||
| + | double lag=1; | ||
| + | for(i=0;i<n;i++) | ||
| + | { if(i==j) continue; | ||
| + | lag*=(x-data[i].x) / (data[j].x-data[i].x) ; | ||
| + | } | ||
| + | </source> | ||
| + | Ak máme <math>\ell_j(x)</math> vypočítané, môžeme vypočítať výsledný súčet Lagrangeových bázových polynómov. Označme si Lagrangeov polynóm L(x) ako premennú ''lag_pol'': | ||
| + | <source lang="c"> | ||
| + | lag_pol=0; | ||
| + | for(j=0;j<n;j++) | ||
| + | { lag=1.0; | ||
| + | //vypocet bazoveho polynomu | ||
| + | for(i=0;i<n;i++) | ||
| + | { if(i==j) continue; | ||
| + | lag*=(x-data[i].x) / (data[j].x-data[i].x) ; | ||
| + | } | ||
| + | // vysledna suma bazovych polynomov | ||
| + | lag_pol+= data[j].y*lag; | ||
| + | } | ||
| + | </source> | ||
| + | Výsledná funkcia počítajúca hodnotu interpolačného polynómu v Lagrangeovom tvare v bode x bude mať tvar: | ||
| + | <source lang="c"> | ||
| + | double LagrangeInterpol(Bod *data, int n, double x) | ||
| + | { double lag,lag_pol=0; | ||
| + | int j,i; | ||
| + | for(j=0;j<n;j++) | ||
| + | { lag=1.0; | ||
| + | for(i=0;i<n;i++) | ||
| + | { if(i==j) continue; | ||
| + | lag*=(x-data[i].x) / (data[j].x-data[i].x) ; | ||
| + | } | ||
| + | lag_pol+= data[j].y*lag; | ||
| + | } | ||
| + | return lag_pol; | ||
| + | } | ||
| + | </source> | ||
| + | ===Newtonov tvar interpolačného polynómu=== | ||
| + | :<math>\begin{align} | ||
| + | & N\left( x \right)={{f}_{0}}+\sum\limits_{j=1}^{n}{{{n}_{j-1}}\left( x \right)\left[ {{x}_{0}},{{x}_{1}},...,{{x}_{j}} \right]} \\ | ||
| + | & {{n}_{j}}\left( x \right)=\prod\limits_{i=0}^{j}{\left( x-{{x}_{i}} \right)} \\ | ||
| + | \end{align}</math> | ||
| + | |||
| + | Rozdielové diferencie môžeme graficky znázorniť ako: | ||
| + | ;f[x1,x2]:[[Súbor:rodielova diferencia 1.png]] | ||
| + | ;f[x2,x3]:[[Súbor:rodielova diferencia 2.png]] | ||
| + | ;f[x1,x2,x3]:[[Súbor:rodielova diferencia 3.png]] | ||
| + | ;f[x1,x2,x3,x4]:[[Súbor:rodielova diferencia 4.png]] | ||
| + | |||
| + | Pri implementácii Newtovového tvaru interpolačného polynómu budeme potrebovať len nasledujúce rozdielové diferencie: | ||
| + | |||
| + | [[Súbor:rodielova diferencia 5.png]] | ||
| + | |||
| + | Pri implementácii interpolačného polynómu v Newtonovom tvare si ako prvé vypočítame potrebné rozdielové diferencie. Podľa prechádzajúcej analýzy potrebujeme nasledujúce rozdielové diferencie: | ||
| + | : <math>f[x_0]</math>, <math>f[x_0,x_1]</math>, <math>f[x_0,x_1,x_2]</math>, ..., <math>f[x_0,x_1, ... , x_{n-1}]</math> | ||
| + | Pri ich výpočte môžeme postupovať nasledovne: | ||
| + | *vytvoríme si pomocné pole hodnôt y-vých súradníc vstupných bodov. Veľkosť poľa bude n. V prípade, ak máme k dispozícii 4 vstupné body, bude toto pole vyzerať nasledovne: | ||
| + | {| class=wikitable | ||
| + | |- | ||
| + | |style="background-color:yellow"|<math>y_0</math> | ||
| + | |<math>y_1</math> | ||
| + | |<math>y_2</math> | ||
| + | |<math>y_3</math> | ||
| + | |} | ||
| + | Poznámka: Žlto zvýraznené bunky poľa predstavujú potrebné rozdielové diferencie a tieto bunky v priebehu výpočtu už meniť nebudeme. | ||
| + | |||
| + | V nasledujúcom kroku vypočítame prvé rozdielové diferencie: <math>f[x_0,x_1]</math>, <math>f[x_1,x_2]</math>, <math>f[x_2,x_3]</math>. Tieto hodnoty uložíme do pomocného poľa na nasledovné pozície: | ||
| + | |||
| + | {| class=wikitable | ||
| + | |- | ||
| + | |style="background-color:yellow"|<math>y_0</math> | ||
| + | |style="background-color:yellow"|<math>f[x_0,x_1]</math> | ||
| + | |<math>f[x_1,x_2]</math> | ||
| + | |<math>f[x_2,x_3]</math> | ||
| + | |} | ||
| + | V ďalšej iterácii vypočítame rozdielové diferencie <math>f[x_0,x_1,x_2]</math>, <math>f[x_1,x_2,x_3]</math>: | ||
| + | {| class=wikitable | ||
| + | |- | ||
| + | |style="background-color:yellow"|<math>y_0</math> | ||
| + | |style="background-color:yellow"|<math>f[x_0,x_1]</math> | ||
| + | |style="background-color:yellow"|<math>f[x_0,x_1,x_2]</math> | ||
| + | |<math>f[x_1,x_2,x_3]</math> | ||
| + | |} | ||
| + | V poslednej iterácii vypočítame rozdielov[ diferenciu <math>f[x_0,x_1,x_2,x_3]</math>: | ||
| + | {| class=wikitable | ||
| + | |- | ||
| + | |style="background-color:yellow"|<math>y_0</math> | ||
| + | |style="background-color:yellow"|<math>f[x_0,x_1]</math> | ||
| + | |style="background-color:yellow"|<math>f[x_0,x_1,x_2]</math> | ||
| + | |style="background-color:yellow"|<math>f[x_0,x_1,x_2,x_3]</math> | ||
| + | |} | ||
| + | Takto máme v pomocnom poli pripravené všetky rozdielové diferencie. Implementácia v jazyku C môže byť nasledovná: | ||
| + | <source lang="c"> | ||
| + | double *koef=new double[n]; // pomocne pole | ||
| + | for(int i=0;i<n;i++) | ||
| + | koef[i]=data[i].y; // na zaciatku ho naplnime y-hodnotami | ||
| + | |||
| + | for(int j=0;j<n-1;j++) // pocitame rozdielove diferencie | ||
| + | { for(int i=n-1;i>j;i--) | ||
| + | koef[i]=(koef[i]-koef[i-1])/(data[i].x-data[i-j-1].x); | ||
| + | } | ||
| + | </source> | ||
| + | Ďalšia vec, ktorú musíme naprogramovať je výpočet bázových polynómov <math> {{n}_{j}}\left( x \right)</math>. Vytvoríme si funkciu ''n_k'', ktorá bude počítač pre hodnotu netonových bázových polynómov. Vstupnými parametrami funkcie budú body interpolácie, hodnota ''j'', ktorá hovorí o stupni polynómu a bod ''x'', pre ktorom chceme zistiť hodnotu bázového Newtovového polynómu. | ||
| + | <source lang="c"> | ||
| + | double n_k(Bod *data,int j, double x) | ||
| + | { | ||
| + | double n_j=1; | ||
| + | for(int i=0;i<j;i++) | ||
| + | n_j*=(x-data[i].x); | ||
| + | return n_j; | ||
| + | } | ||
| + | </source> | ||
| + | Výsledné riešenie môže mať tvar: | ||
| + | <source lang="c"> | ||
| + | double NewtonPol(Bod *data, int n,double x) | ||
| + | { | ||
| + | double val=0; | ||
| + | double *koef=new double[n]; | ||
| + | for(int i=0;i<n;i++) | ||
| + | koef[i]=data[i].y; | ||
| + | |||
| + | for(int j=0;j<n-1;j++) | ||
| + | { for(int i=n-1;i>j;i--) | ||
| + | koef[i]=(koef[i]-koef[i-1])/(data[i].x-data[i-j-1].x); | ||
| + | } | ||
| + | for(int i=0;i<n;i++) | ||
| + | val+=koef[i]*n_k(data,i,x); | ||
| + | |||
| + | delete koef; | ||
| + | return val; | ||
| + | } | ||
| + | </source> | ||
| + | ==Vstupné údaje== | ||
| + | Pre účel zadania použime nasledujúce vstupné hodnoty: | ||
| + | n = 8 | ||
| + | {| class=datatable | ||
| + | |- | ||
| + | !<math>x_i</math> | ||
| + | !<math>y_i</math> | ||
| + | |- | ||
| + | |1.0 | ||
| + | | -1.71828 | ||
| + | |- | ||
| + | |1.3 | ||
| + | | -0.8132 | ||
| + | |- | ||
| + | |2.1 | ||
| + | |11.28193 | ||
| + | |- | ||
| + | |3.8 | ||
| + | |163.8124 | ||
| + | |- | ||
| + | |4.55 | ||
| + | |333.9611 | ||
| + | |- | ||
| + | |5.0 | ||
| + | |476.5868 | ||
| + | |- | ||
| + | |6.7 | ||
| + | |1202.706 | ||
| + | |- | ||
| + | |7.9 | ||
| + | |1197.726 | ||
| + | |} | ||
| + | Poznámka: vstupné bodu patria funkcii <math>4x^3-e^x</math> | ||
Verzia zo dňa a času 17:26, 16. apríl 2010
Obsah
Zadanie
Riešte problém interpolácie dát. K dispozícii máme n bodov v priestore (x,y). Overte tvrdenie, že existuje len jeden interpolačný polynóm najnižšieho stupňa (n-1) pre n bodov v rovine. Inak povedané, overte že Lagrangeov a Newtonov interpolačný polynóm sú len 2 rôzne zápisy pre jediný polynóm.
Analýza
Interpolačný polynóm v Lagrangeovom a Newtonovom tvare sú opísané v kapitole Algoritmy interpolácie.
Lagrangeov tvar interpolačného polynómu
- [math]L(x) := \sum_{j=0}^{n} y_j \ell_j(x)[/math]
- [math]\ell_j(x) := \prod_{i=0,\, i\neq j}^{n} \frac{x-x_i}{x_j-x_i} = \frac{(x-x_0)}{(x_j-x_0)} \cdots \frac{(x-x_{j-1})}{(x_j-x_{j-1})} \frac{(x-x_{j+1})}{(x_j-x_{j+1})} \cdots \frac{(x-x_{n})}{(x_j-x_{n})}.[/math]
Postup pri implementácii algoritmu:
Pri výpočte lagrangeovho interpolačného polynómu musíme začať pri výpočte lagrangeových bázových polynómov [math]\ell_j(x)[/math]. Ich výpočet je jednoduchý. Označme si [math]\ell_j(x)[/math] ako lag. Vstupné údaje sú v poli štruktúr (data) typu Bod o veľkosti n.
double lag=1;
for(i=0;i<n;i++)
{ if(i==j) continue;
lag*=(x-data[i].x) / (data[j].x-data[i].x) ;
}
Ak máme [math]\ell_j(x)[/math] vypočítané, môžeme vypočítať výsledný súčet Lagrangeových bázových polynómov. Označme si Lagrangeov polynóm L(x) ako premennú lag_pol:
lag_pol=0;
for(j=0;j<n;j++)
{ lag=1.0;
//vypocet bazoveho polynomu
for(i=0;i<n;i++)
{ if(i==j) continue;
lag*=(x-data[i].x) / (data[j].x-data[i].x) ;
}
// vysledna suma bazovych polynomov
lag_pol+= data[j].y*lag;
}
Výsledná funkcia počítajúca hodnotu interpolačného polynómu v Lagrangeovom tvare v bode x bude mať tvar:
double LagrangeInterpol(Bod *data, int n, double x)
{ double lag,lag_pol=0;
int j,i;
for(j=0;j<n;j++)
{ lag=1.0;
for(i=0;i<n;i++)
{ if(i==j) continue;
lag*=(x-data[i].x) / (data[j].x-data[i].x) ;
}
lag_pol+= data[j].y*lag;
}
return lag_pol;
}
Newtonov tvar interpolačného polynómu
- [math]\begin{align} & N\left( x \right)={{f}_{0}}+\sum\limits_{j=1}^{n}{{{n}_{j-1}}\left( x \right)\left[ {{x}_{0}},{{x}_{1}},...,{{x}_{j}} \right]} \\ & {{n}_{j}}\left( x \right)=\prod\limits_{i=0}^{j}{\left( x-{{x}_{i}} \right)} \\ \end{align}[/math]
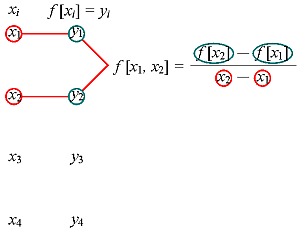
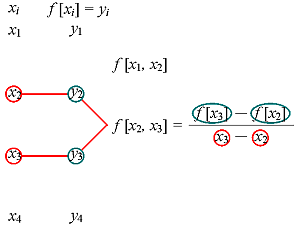
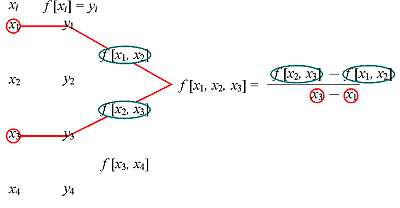
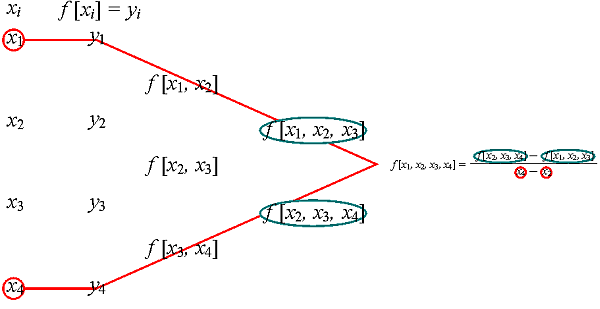
Rozdielové diferencie môžeme graficky znázorniť ako:
Pri implementácii Newtovového tvaru interpolačného polynómu budeme potrebovať len nasledujúce rozdielové diferencie:
Pri implementácii interpolačného polynómu v Newtonovom tvare si ako prvé vypočítame potrebné rozdielové diferencie. Podľa prechádzajúcej analýzy potrebujeme nasledujúce rozdielové diferencie:
- [math]f[x_0][/math], [math]f[x_0,x_1][/math], [math]f[x_0,x_1,x_2][/math], ..., [math]f[x_0,x_1, ... , x_{n-1}][/math]
Pri ich výpočte môžeme postupovať nasledovne:
- vytvoríme si pomocné pole hodnôt y-vých súradníc vstupných bodov. Veľkosť poľa bude n. V prípade, ak máme k dispozícii 4 vstupné body, bude toto pole vyzerať nasledovne:
| [math]y_0[/math] | [math]y_1[/math] | [math]y_2[/math] | [math]y_3[/math] |
Poznámka: Žlto zvýraznené bunky poľa predstavujú potrebné rozdielové diferencie a tieto bunky v priebehu výpočtu už meniť nebudeme.
V nasledujúcom kroku vypočítame prvé rozdielové diferencie: [math]f[x_0,x_1][/math], [math]f[x_1,x_2][/math], [math]f[x_2,x_3][/math]. Tieto hodnoty uložíme do pomocného poľa na nasledovné pozície:
| [math]y_0[/math] | [math]f[x_0,x_1][/math] | [math]f[x_1,x_2][/math] | [math]f[x_2,x_3][/math] |
V ďalšej iterácii vypočítame rozdielové diferencie [math]f[x_0,x_1,x_2][/math], [math]f[x_1,x_2,x_3][/math]:
| [math]y_0[/math] | [math]f[x_0,x_1][/math] | [math]f[x_0,x_1,x_2][/math] | [math]f[x_1,x_2,x_3][/math] |
V poslednej iterácii vypočítame rozdielov[ diferenciu [math]f[x_0,x_1,x_2,x_3][/math]:
| [math]y_0[/math] | [math]f[x_0,x_1][/math] | [math]f[x_0,x_1,x_2][/math] | [math]f[x_0,x_1,x_2,x_3][/math] |
Takto máme v pomocnom poli pripravené všetky rozdielové diferencie. Implementácia v jazyku C môže byť nasledovná:
double *koef=new double[n]; // pomocne pole
for(int i=0;i<n;i++)
koef[i]=data[i].y; // na zaciatku ho naplnime y-hodnotami
for(int j=0;j<n-1;j++) // pocitame rozdielove diferencie
{ for(int i=n-1;i>j;i--)
koef[i]=(koef[i]-koef[i-1])/(data[i].x-data[i-j-1].x);
}
Ďalšia vec, ktorú musíme naprogramovať je výpočet bázových polynómov [math] {{n}_{j}}\left( x \right)[/math]. Vytvoríme si funkciu n_k, ktorá bude počítač pre hodnotu netonových bázových polynómov. Vstupnými parametrami funkcie budú body interpolácie, hodnota j, ktorá hovorí o stupni polynómu a bod x, pre ktorom chceme zistiť hodnotu bázového Newtovového polynómu.
double n_k(Bod *data,int j, double x)
{
double n_j=1;
for(int i=0;i<j;i++)
n_j*=(x-data[i].x);
return n_j;
}
Výsledné riešenie môže mať tvar:
double NewtonPol(Bod *data, int n,double x)
{
double val=0;
double *koef=new double[n];
for(int i=0;i<n;i++)
koef[i]=data[i].y;
for(int j=0;j<n-1;j++)
{ for(int i=n-1;i>j;i--)
koef[i]=(koef[i]-koef[i-1])/(data[i].x-data[i-j-1].x);
}
for(int i=0;i<n;i++)
val+=koef[i]*n_k(data,i,x);
delete koef;
return val;
}
Vstupné údaje
Pre účel zadania použime nasledujúce vstupné hodnoty: n = 8
| [math]x_i[/math] | [math]y_i[/math] |
|---|---|
| 1.0 | -1.71828 |
| 1.3 | -0.8132 |
| 2.1 | 11.28193 |
| 3.8 | 163.8124 |
| 4.55 | 333.9611 |
| 5.0 | 476.5868 |
| 6.7 | 1202.706 |
| 7.9 | 1197.726 |
Poznámka: vstupné bodu patria funkcii [math]4x^3-e^x[/math]