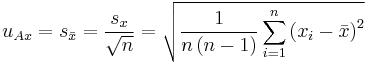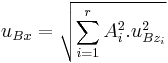Základná klasifikácia neistôt merania, charakteristika jednotlivých druhov a možnosti ich zmenšovania

Tento článok patrí do časti Kolokviálna skúška. Materiály tu uvedené sú prípravou na záverečnú štátnu (kolokviálnu) skúšku v študijnom zameraní Manažérstvo kvality produkcie na Fakulte mechatroniky TnUAD.

Prehľad a definície

Neistota merania Je to parameter priradený k výsledkom merania, ktorý charakterizuje rozptyl hodnôt, ktoré sa môžu oddvôvodnene priraďovať k meranej veličine napr. výberová smerodajná odchýlka.

Predstavuje interval okolo odhadu meranej veličiny v ktorom sa nachádza skutočná hodnota meranej veličiny s určitou pravdepodobnosťou.

Pri určovní neistôt vychádzame t teórie pravdepodobnosti a matematickej štatistiky. Predpokladáme, že namerané hodnoty, ako aj chyby majú určité rozdelenie pravdepodobnosti.

Merané veličiny sú konkrétne veličiny, ktoré sú predmetom merania, pričom vstupná veličina Y je závislá od niekoľkých výstupných veličín Xi=(i=1,2,...,N) podľa funkčného vzťahu:

Y=f(X1,X2,....,Xn) (1)

Modelová funkcia f reprezentuje postup merania a metódu vyhodnotenia. Vyjadruje, ako sa z hodnôt Xi získavajú hodnoty výstupnej veličiny Y. Teda: Y=odhad výstupnej veličiny Xi=odhad vstupných veličín f=známy funkčný vzťah Pre náhodné veličiny sa používa ako miera rozptýlenia hodnôt rozptyl ich rozdelenia alebo jeho kladná druhá odmocnina nazývaná smerodajná odchýlka

Štandardná neistota merania vstupného odhadu alebo výsledku merania y, označená ako u(y) - základná kvantitatívna charakteristika neistoty, je smerodajnou odchýlkou meranej veličiny Y. Treba ju určiť z odhadov xi vstupných veličín Xi a k nim pridružených štandardných neistôt u(xi)

Absolútna štandardná neistota (ux)- štandardná neistota vyjadrená v jednotkách meranej veličiny, x je veličina, ktorá je meraná; napr.: ut absolútna štandardná neistota teploty

Relatívna štandardná neistota (urx) - podiel absolútnej neistoty a odhadu hodnoty meranej veličiny, štandardná neistota merania odhadu vydelená modulom (absolútnou hodnotou)tohto odhadu a preto je bezrozmerná. Nemožno ju však použiť v prípade, ak sa odhad rovná nule.

Vyhodnocovanie neistôt meraní vstupných veličín

Neistota výsledkov merania sa skladá z čiastočných zložiek:

1. Štatistické spracovanie nameraných hodnôt (metóda typu A)
2. Iné ako štatistické spracovanie nameraných údajov (metóda typu B)
3. Kombinovaná neistota[1]

Variabilita nameraných hodnôt má dve základné príčiny, ktoré väčšinou pôsobia súčasne:

1. vlastnosti vyšetrovaného javu(napr. neodstrániteľná nehomogenita vyšetrovaného materiálu, fluktuácie vyvolané fyzikálnymi procesmi a pod.),
2. technické nedostatky meracej metódy(nepresnosť meracieho zariadenia, nepresnosť pri príprave vzoriek, zmeny prostredia v ktorom meriame t. j. teplota, vlhkosť vzduchu a pod., a tiež vplyv osôb, ktorí sa experimentu, merania zúčastňujú).

Treba sa teda snažiť o udržanie najstabilnejších podmienok pri meraní

Medzi zdroje neistôt pri meraní patria:

1. neúplná definícia meranej veličiny,
2. nedokonalá realizácia definície meranej veličiny,
3. nereprezentatívny výber vzoriek
4. nedostatočne známe účinky podmienok prostredia alebo ich nedokonalé meranie,
5. subjektívnosť odčítavania z analógových prístrojov,
6. nepresnosť etalónov a referenčných materiálov
7. aproximácie a predpoklady zahrnuté v metóde a postupe merania,
8. zmeny pri opakovaných meraniach meranej veličiny v rovnakých podmienkach.

Štatistické spracovanie nameraných hodnôt(metóda typu A)

Jej pôvod je v náhodných (neobjasnených) vplyvoch, pôsobiacich na výsledok merania xI. Číselne je totožná so smerodajnou odchýlkou strednej hodnoty xI výsledku merania vstupnej veličiny XI. Táto predstavuje hodnotu získanú z najlepšieho odhadu rozptylu štatistického výberu s normálnym rozdelením. Vyhodnotenie typu A vychádza zo štatistickej analýzy opakovaných meraní údajov. Príčiny týchto neistôt sú na rozdiel od typu B neznáme. Pre túto metódu je typické, že rastúcim meraním ich hodnoty klesajú. Ak opakujeme meranie veličiny, odhad výslednej hodnoty reprezentuje hodnota výberového (aritmetického) priemeru, ktorý sa vypočíta rovnako ako vo vzťahu (2). Štandardná neistota metódou A sa rovná smerodajnej odchýlke výslednej hodnoty, čiže aritmetického priemeru.[4]

(2)

Ak použijeme malý počet opakovaných meraní (n < 10) je hodnota podľa vzťahu (2) málo spoľahlivá. Preto použijeme metódu B, ktorá nie je založená na štatistických metódach.

Iné ako štatistické spracovanie nameraných údajov(metóda typu B)

Každá neistota výsledku merania xI , určená iným než „štatistickým“ postupom, je neistotou typu B. Vyznačuje sa najmä týmito znakmi:

1. viaže sa na známe a teda identifikovateľné zdroje náhodných chýb, majúce svoj pôvod v:
   1. použitých mierach a meracích prostriedkoch, resp. nemožnosti určiť ich „absolútne presnú“ hodnotu,
   2. rozdieloch medzi modelovou rovnicou merania a reálnym procesom
2. neistotou typu B je zaťažený každá pozorovaná hodnota xIi
3. neistoty typu B je treba považovať za veličiny pochádzajúce z určitého rozptylu hodnôt. V dôsledku toho majú taktiež charakter smerodajnej odchýlky.

Neistoty typu B sa viažu na známe, identifikovateľné zdroje. Odhaduje sa na základe možných dostupných informácii ako sú údaje na meracích prostriedkoch, zistenia z predchádzajúcich meraní, z neistoty referenčných údajov, zo skúsenosti o meranom objekte.Táto metóda na rozdiel od typu A nie je závislá od počtu meraní. Pri neistote typu B vychádzame z čiastkových neistôt jednotlivých zdrojov uBzi. Ak je známa maximálna odchýlka i-teho zdroja neistoty zimax, neistota uBzi sa určí zo vzťahu:

(3)

kde k je súčiniteľ vychádzajúci zo zákona rozdelenia, Ak je hodnota štandardnej neistoty uBzi známa, výsledná hodnota pre r zdrojov sa určí podľa vzťahu

(4)

kde uBzi sú neistoty jednotlivých zdrojov (m), Ai ich súčinitele citlivosti.

Kombinovaná neistota

V praxi si málokedy vystačíme iba s jedným alebo iba druhým typom neistoty zvlášť. Preto je potrebné určiť výsledný efekt kombinovaných neistôt merania oboch typov.Keďže sa teda nedá použiť iba jeden typ neistoty, používa sa kombinovaná neistota, oboch typov neistôt A aj B, pričom jej vzťah môžeme uviesť ako:

(5)

Štandardné neistoty vytvárajú interval pokrývajúci skutočnú hodnotu s pomerne malou pravdepodobnosťou. Preto ak chceme vytvoriť interval s pravdepodobnosťou pokrytia skutočnej hodnoty blízkej 100% treba použiť koeficient rozšírenia k. Takáto neistota sa nazýva rozšírená neistota U. Matematické vyjadrenie U=ku kde •U je rozšírená neistota (m),

•k je koeficient rozšírenia,

•u je štandardná neistota (m).

Koeficient rozšírenia sa volí podľa požadovaného intervalu. Pre k = 2 je pravdepodobnosť približne 95%, k = 3 je 99,7%.[4]

Presnosť merania možno zlepšiť jednak predĺžením trvania merania, alebo vykonaním viacnásobného počtu meraní.

Použitá literatúra

[1]http://www.snas.sk/files/msa/MSA_L12_Vyjadr_neistot_merania_kalib_A1SK.pdf

[2]http://www.snas.sk/files/msa/MSA_L11.pdf

[3]http://www.kar.elf.stuba.sk/predmety/iss/pdf/neistoty.pdf

[4]http://kiwiki.fmtnuni.sk/mediawiki/index.php/Metrol%C3%B3gia,_meranie,_chyby_a_neistoty_v_meran%C3%AD