Triedenie delením

Algoritmy a programovanie

---

Dátový typ

Štruktúry

Rekurzia

Algoritmy vyhľadávania

Algoritmy triedenia

>Triedenie výmenou
>Triedenie vkladaním
>Triedenie zlučovaním
>Triedenie delením
>Triedenie výberom
>Triedenie - ostatné princípy

Lineárny zoznam

Binárny strom

Numerické algoritmy

Grafové algoritmy

Quick sort

Quicksort alebo triedenie delením je jeden z najrýchlejších známych triediacich algoritmov, založených na porovnávaní prvkov. Jeho priemerná doba výpočtu je O(n.log n) a je najlepšia zo všetkých podobných algoritmov. Jeho naprogramovanie je aj celkom jednoduché. Nevýhodou je, že pri nevhodnom usporiadaní vstupných dát môže byť časová a pamäťová náročnosť tohto algoritmu až [math]O(n^2)[/math].

Princíp algorimtu

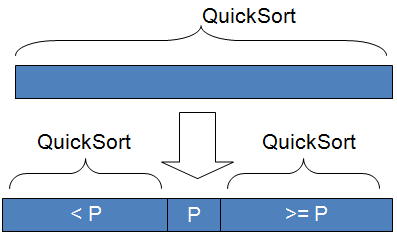
Základnou myšlienkou quicksortu je rozdelenie triedenej postupnosti čísel na dve približne rovnaké časti. V jednej časti sú čísla väčšie a v druhej menšie ako istá zvolená hodnota, ktorá sa nazýva pivot. Ak je táto hodnota zvolená dobre, sú obe časti približne rovnako veľké. Ak budú obe časti samostatne roztriedené, je roztriedené i celé pole. Obe časti sa potom rekurzívne triedia rovnakým spôsobom.

Najväčším problémom celého algoritmu je voľba pivotu. Ak sa podarí zvoliť číslo blízke mediánu triedenej časti poľa, je algoritmus najrýchlejší. Ak nie, je jeho pamäťová a časová náročnosť vyššia, ako pri všetkých ostatných algoritmov.

Vlastnosti algoritmu

Čas behu algoritmu je v priemernom prípade O(n log n). Dobrá časová zložitosť algoritmu spočíva v správnom výbere pivota. V ideálnom prípade je to medián (alebo hodnota blízka mediánu).Ak však je pivot zakaždým minimum alebo maximum daného podpoľa, časová zložitosť narastá na O(n2). Preto je vhodné použiť na výber pivota jednu z nasledujúcich techník:

1. Náhodný prvok – často používaná metóda. Ak ide o naozaj náhodný výber, čas triedenia je O(n log n).
2. Metóda mediánu z troch čísel (prípadne z ľubovolného konštantného počtu) – vyberú sa z množiny tri prvky, z ktorých sa nájde medián a ten sa zvolí za pivota.

Qucksort nie je stabilné triedenie.

Vzorový príklad

Princíp algorimu Quick sort v pseudokóde

QuickSort (pole data, index lavy, index pravy)
begin	
   ak lavy<pravy
   	int m;
 	// rozdel pole vzhladom k pivotu; m – index pivota
	// nalavo od P budu cisla mensie ako P
	// napravo od P budu prvky vasie ako P
	QuickSort(data, lavy, m-1);
	QuickSort(data, m+1, pravy);
   
end

Usporiadanie poľa vzhľadom na pivota

Uvažujem pole, ktoré budeme triediť. Na začiatku aplikujeme algoritmus Quicksort na cele pole, tada od indexu (lavy) 0 po index (pravy) n-1, kde n je veľkosť triedeného poľa.

index	0	1	2	3	4	5	6
hodnota	18	2	39	6	40	4	20

1) Určíme pivota. Pivot bude prvok v strede. Stredný prvok vypočítame ako (index ľavého prvku + index pravého prvku)/2, kde indexy ľavý a pravý nám hovoria o intervale triedenia.

pivot=pole[(0+6)/2]=pole[3]=6

Označme pivota žltým pozadím.

2) Pole usporiadame tak, aby naľavo od pivota boli prvky menšie ako pivot a napravo od pivota prvky väčšie ako pivot. Dosiahneme to tak, že si označíme tie prvky, ktoré na danú stranu poľa nepatria. Indexom i si označíme prvý prvok v ľavej časti, ktorý tam nepatrí a indexom j si onzačíme prvý prvok (sprava) v pravej časti, ktorý tam nepatrí. Samotná implementácia je nasledovná:

1. zväčšuj index i, pokiaľ platí že [math]prvok_i[/math] < pivot
2. zmenšuj index j, pokiaľ platí že [math]prvok_j[/math] > pivot

Indexy i a j sa zastavia na prvkoch, ktorý nevyhovujú danej podmienke.

18	2	39	6	40	4	20
i					j

3) Ak platí, že i<=j, tak prvky na indexe i a j vzájomne zameníme. Index i zväčšíme o 1 a index j zmenšíme o 1.

4	2	39	6	40	18	20
	i			j

Opakujeme kroky 2) a 3), pokiaľ platí, že i<=j. Tieto kroky uvádzame v nasledujúcich tabuľkách:

Prvok 39 nepatrí na ľavú stranu. Podľa podmienky č.2 v kroku 2, index j zmenšíme ako platí [math]prvok_j[/math] < pivot. Index j teda zmenšíme o 1.

4	2	39	6	40	18	20
		i	j

Vymeníme prvky na indexoch i a j. Index i zväčšíme o 1 a index j zmenšíme o 1.

index	0	1	2	3	4	5	6
hodnota	4	2	6	39	40	18	20
rozdelenie			j	i

Keďže teraz platí, že i>j, ďalšie posúvanie indexov nerobíme a teraz prichádza rekurzívna časť algoritmu. Aplikujeme algoritmus Quicksort na časť pola od indexu lavy po j, a od indexu i po pravy.

Quicksort(data,0,2) index 0 1 2 hodnota 4 2 6 lavy=0 pravy=2 pivot=data[(lavy+pravy)/2]=data[1]=2 Usporiadanie vzhľadom na pivota: index 0 1 2 hodnota 4 2 6 rozdelenie i j Výmena prvkov na indexoch i a j: index 0 1 2 hodnota 2 4 6 rozdelenie j i Rekurzívne volanie funkcie Quicksort: Quicksort(data,0,1) // (lavy, j) Quicksort(data,2,2) // (i, pravy)

Quicksort(data,3,6) index 3 4 5 6 hodnota 39 40 18 20 lavy=3 pravy=6 pivot=data[(lavy+pravy)/2]=data[4]=40 Usporiadanie vzhľadom na pivota: index 3 4 5 6 hodnota 39 40 18 20 rozdelenie i j Výmena prvkov na indexoch i a j: index 3 4 5 6 hodnota 39 20 18 40 rozdelenie i, j Opäť posúvame indexy i a j podľa zadefinovaných pravidiel. Po tomto posúvaní budú hodnoty i a j nasledovné: index 3 4 5 6 hodnota 39 20 18 40 rozdelenie j i Prvky na indexe i a j už nezameníme, pretože podmienka v kroku 3 (i<=j) nie je splnená. Rekurzívne volanie funkcie Quicksort: Quicksort(data,3,5) // (lavy, j) Quicksort(data,6,6) // (i, pravy)

Ďalšie kroky algoritmu si jednoducho odvodíte sami.

Implementácia v jazyku C

 1 void QuickSort(int data[ ],int lavy, int pravy)
 2 {
 3    if(lavy<pravy)
 4    {   
 5       int i = lavy, j = pravy, p = data[ (lavy + pravy) / 2 ];
 6       do {
 7           while (data[ i ] < p) i++;
 8           while (p < data[ j ]) j--;
 9           if (i <= j) 
10 	  {    SWAP(data[ i ], data[ j ]);
11                i++; j--;
12           }
13       } while (i <= j);
14       QuickSort(data, lavy, j);
15       QuickSort(data, i, pravy);
16    }
17 }