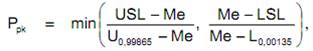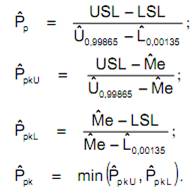SPC pri nesplnení predpokladov normálneho rozdelenia pravdepodobností znaku kvality

Tento článok patrí do časti Kolokviálna skúška. Materiály tu uvedené sú prípravou na záverečnú štátnu (kolokviálnu) skúšku v študijnom zameraní Manažérstvo kvality produkcie na Fakulte mechatroniky TnUAD.

Ukazovatele spôsobilosti a výkonnosti v prípade nenormálneho rozdelenia znaku kvality

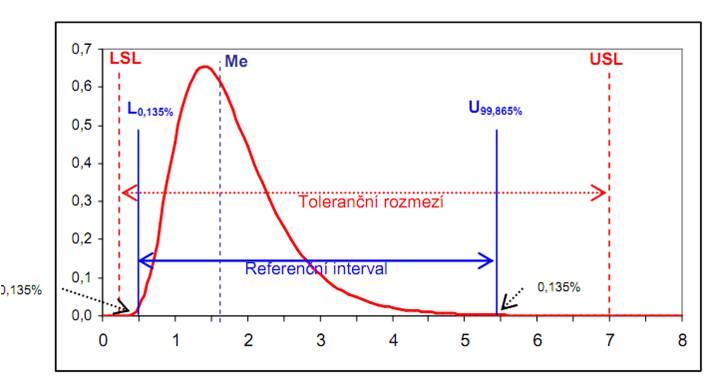
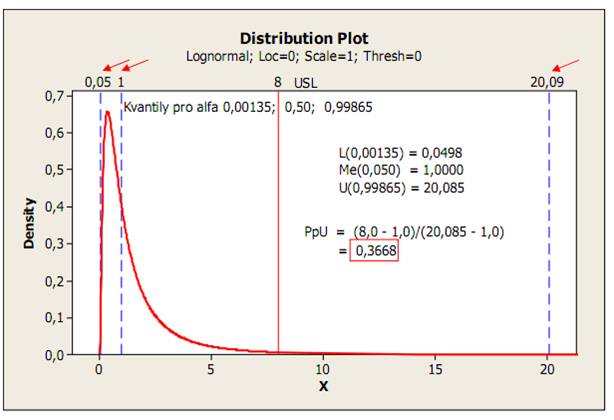
V niektorých prípadoch sa nedá použiť normálne rozdelenie. Napríklad pri ovalite, hádzavosti, kolmosti, rovinnosti, sile, veľkosti uhlu a pod.. Tu sa dajú aplikovať iné modely, ako napr. logaritmicko – normálne rozdelenie, Weibullovo rozdelenie, preklopené normálne rozdelenie a pod. Je ale nutné overiť, že onen daný typ rozdelenia pravdepodobnosti sa u tohto znaku kvality objavuje stále, je proste charakteristickým rysom jeho chovania. Predpokladajme teda, že znak kvality ide popísať rozdelením pravdepodobnosti s istou hustotou pravdepodobnosti. Ako potom definovať zodpovedajúce ukazovatele C_p, C_pk, P_p a P_pk? Najprv si ujasníme, že v prípade nenormálneho rozdelenia dát ukazovatele C_p a C_pk strácajú zmysel. Je to spôsobené tým, že tieto ukazovatele využívajú smerodajnú odchýlku inherentnej variability. Aj keď dáta budú zbierané vo forme podskupín, odhady smerodajnej odchýlky v rámci podskupín založenej na výberovom rozpätí R či výberovej smerodajnej odchýlky s strácajú u nenormálnych rozdeleniach zmysel, pretože smerodajná odchýlka u týchto nenormálnych rozdelení nemá tú vlastnosť ako smerodajná odchýlka u normálneho rozdelenia N(μ,σ²), totiž, že interval (μ- 3σ, μ+3) dĺžky 6σ pokrýva hodnoty normálne rozdelenej náhodnej veličiny s pravdepodobnosti 0,9973. Tento interval musí byť u nenormálneho rozdelenia nahradený niečím iným. Tu sa využíva kvantilové rozpätie U_0,99865 – L_0,00135, Kde U_0,99865 je horný kvantil a L_0,00135 je dolný kvantil odvodený od rozdelenia pravdepodobnosti nenormálne rozdeleného znaku kvality. Toto kvantilové rozpätie pokrýva podiel 0,9973 všetkých potenciálnych jednotiek základného súboru nenormálneho rozdeleného, rovnako ako pokrýva interval 6 σ (tj. - 3 σ až +3σ okolo μ) v prípadoch, kde znak kvality v základnom súbore je rozdelený normálne. Na obrázku je zakreslený zodpovedajúci referenčný interval , kde pod dolnou hodnotou kvantilu sa očakáva 0,135% všetkých možných jednotiek, rovnako ako nad hornou hodnotou kvantilu . Potom ukazovateľ výkonnosti P_p je definovaný ako:

Podobne je definovaný ukazovateľ P_pk:

Kde Me je medián (t.j. 0,5 – kvantil, môžeme tiež písať Me_0,5, alebo ako kvantil Me_50% V praxi je treba získať odhady kvantilov, potom ide vypočítať odhady ukazovateľov výkonnosti:

Pri získavaní odhadov týchto ukazovateľov výkonnosti P_p a P_pk na základe napozorovaných dát sa stretávame s veľkým problémom, a to , ako získať odhady príslušných kvaltilov.

L0,00135, U0,99865, Me0,5.

Usporiadanie dát do podskupín tu nehrá rolu, pretože všetky dáta potrebujeme usporiadať podľa veľkosti pre získanie odhadov vyššie uvažovaných kvantilov. Pretože odhady kvantilov zodpovedajúce buď veľmi veľkému alebo veľmi malému percentu budú viac nestabilné, javí sa ako schodnejšia cesta, najprv z dát odhadnúť typ rozdelenia a jeho parametre a potom urobiť odhady príslušných kvantilov, čo mnohé štatistické softwary umožňujú. Ďalšie doporučenie vychádza z možnosti vhodnej transformácie pôvodných dát na nové dáta už normálne rozdelené. Súčasne sa prevedie i transformácia špecifikačných medziach a výkonnosť procesu sa vyhodnocuje pomocou nových (transformovaných ) dát a tvarov ukazovateľov založených na normalite. Ani v tomto prípade nemajú zmysel ukazovatele spôsobilosti C_p a C_pk, pretože transformácia dát sa obvykle naruší zachovanie zhodnosti úrovne inherentnej variability vo vnútri podskupín, ktorá je zaručená zvládnutím procesu, jeho stabilitou. Transformácia, ktoré sa v praxi najčastejšie používajú (Box – Coxova tranformácia, Johnsonova trieda transformácií, Pearsonové krivky) sú silné nelineárne. Hodnotení spôsobilosti na základe podskupín by malo zmysel jedine vtedy, keby transformované podskupiny opäť vykazovali rovnosť úrovne variability, čo je možné overiť aplikáciou niektorých z testu na rovnosť rozptylu, ako je napr. Bartlettov či Leveneov test. Tento prípad prichádza do úvahy obecne snáď iba u Box-Coxovej transformácie, ktorá je pomerne jednoduchá. Môže ale nastať situácia, že vhodná transformácia nie je nájdená a dáta odolávajú normalite ďalej. Potom dáta budú pozbierané z rôznych zdrojov či pri meniacich sa podmienkach v procese alebo budú nejako upravované či cenzurované, prípadne meranie bolo prevedené málo presne, na málo desatinných miest. Prítomnosť rôznych zdrojov či meniacich sa podmienkach vedie obvykle ku zmiešaniu normálnych rozdelení, ktoré môžu alebo nemusia byť rozložiteľné na jednotlivé podsúbory dát, ktoré ide iba normálnym rozdelením popísať. Jedná sa o tzv. Stratifikáciu dát. Obvykle sa táto stratifikácia dát prevádza podľa rôznych príznakov, ktoré vykazuje výrobný proces. Táto situácia najčastejšie nastáva u výrobných procesov, na ktoré pôsobí rôzne vymedziteľné, teda identifikovateľné príčiny, ktoré sa nedajú alebo ich nevieme z procesu odstrániť (napr. variabilita vstupného materiálu, vplyv prostredia, opotrebovanie či zmena nástroja a pod.) V týchto prípadoch je nutné postupovať veľmi opatrne.

Odhad referenčných medzí v prípade nenormálneho rozdelenia dát :

Pokiaľ individuálne hodnoty sledovaného znaku kvality v procesu sú rozdelené nenormálne, potom pre odhady ukazovateľov výkonnosti je treba odhadnúť kvantity L_0,00135. Ďalej budeme uvažovať prístupy, jak požadované kvantity odhadnúť.

Známe nenormálne rozdelenie

Niekedy je tvar rozdelenia sledovaného znaku kvality známy buď zo skúseností, alebo na základe znalostí fyzikálnych vlastností procesu. Potom je treba podrobiť sledované dáta testu dobré zhody, overiť či predpokladaný model správne vystihuje sledované dáta, odhadnúť parametre rozdelenia a vypočítať potrebné kvantity. Najčastejšie sa tak stretávame s rozdelením log-normálnym, Weibullovým, exponenciálnym a pod. Na obrázku je znázornená situácia, akým spôsobom sa odvodzuje ukazovateľ výkonnosti pre nenormálne rozdelený znak kvality.

Metóda identifikácií rozdelenia

Najprv je potrebné identifikovať rovinu rozdelenia, následne potom parametre rozdelenia, ktoré najlepšie vystihujú napozorované dáta. Dáta je treba stanoviť a vypočítať potrebné kvantily rozdelenia. Identifikované rozdelenia je treba podrobiť testu dobrej zhody, overiť, či naozaj dobre vystihuje rozdelenie experimentálnych dát. Na obrázku 3 je znázornená logaritmicko – normálne rozdelenie. Je nutné si ale uvedomiť, že vlastnosť sledovaného znaku kvality nechať sa opísať nájdeným typom rozdelenia pravdepodobnosti, by sa mala prejaviť v každom prípade analýzy dát získaných jeho meraním. Malo by sa jednať o jeho typickú vlastnosť, ktorá vychádza obvykle z fyzikálnej podstaty jeho chovania.

Metóda pravdepodobnostného papiera

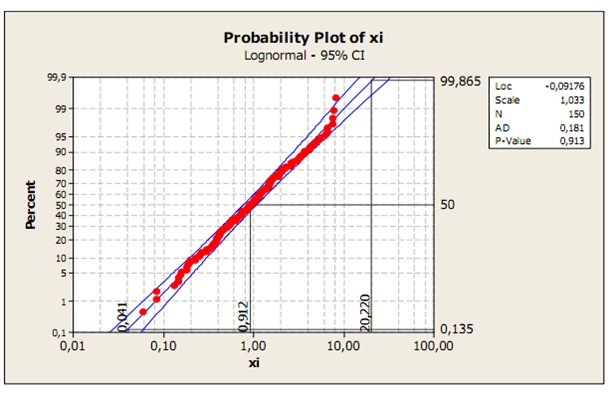
Do pravdepodobnostného papiera, kde stupnica na osi x je lineárna a stupnica na osi y je pravdepodobnostná, odpovedajúca určitému rozdeleniu pravdepodobnosti, sa zakreslí N nameraných hodnôt, usporiadaných podľa veľkosti (x(i)) s odpovedajúcimi hodnotami empirickej distribučnej funkcie ((i)/N). Týmito bodmi preložená priamka je najlepším odhadom distribučnej funkcii predpokladaného rozdelenia pravdepodobnosti študovaného znaku kvality. Na tejto priamke odpočítame príslušné kvantily odpovedajúce zvoleným podielom (0,00135; 0,50; 0,99865) a tie potom dosadíme do výrazu pre odhady ukazovateľov výkonnosti. Ide o grafickú metódu pokiaľ je skutočne použitá iba s pomocou pravdepodobnostného papiera bez softwaru, môže byť aj dosť nepresná.

Metóda Pearsonových kriviek

Ako alternatívna metóda môže byť použitá metóda normalizovaných Pearsonových kriviek pomocou ktorých sa odhadne model rozdelenia sledovaného znaku kvality a vypočítame odhady kvantilov. V prípade použitia tejto metódy je treba počítať vedľa výberového priemeru a výberovej smerodajnej odchýlky i výberovej šikmosti a výberovej špicatosti. Táto metóda, ktorá poskytuje iba približné výsledky, nie je preferovaná pre svoju pracnosť.

Metóda Johnsonovej transformácie

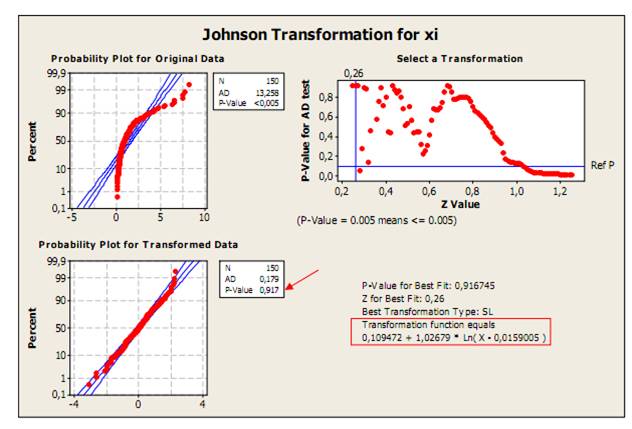
Pokiaľ hodnoty sledovaného znaku kvality nie sú normálne rozdelené, je možné použiť Johnsonovu transformáciu tak, že nové transformované dáta sú potom rozdelené normálne N(0,1). Johnsonova transformácia vyberie jeden zo troch typov rovníc v závislosti na tom, či je náhodná veličina „ohraničená“ – typ SB; „lognormálna“ – typ SL; alebo neohraničená“ – SU. Ide o rovnice : Typ SB: y= a + b. ln((x + c) / (d – x)) pre b >0; -c < x < d. Typ SL: y = a + b.ln (x + c) pre b > 0; -c < x Typ SU: y = a+ b. Asinh((x-c)/d) pre b > 0; d > 0

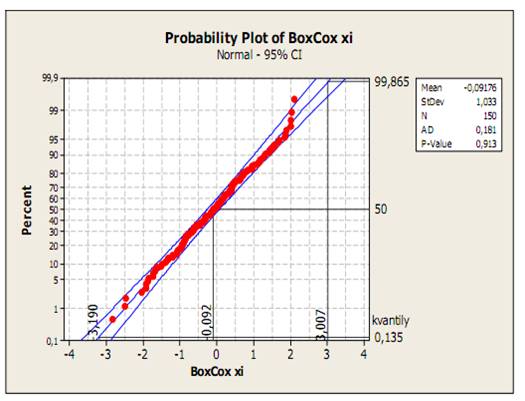
Metóda Box – Coxovej transformácie

Box – Coxova transformácia odhaduje hodnotu λ, ktorá minimalizuje smerodajnú odchýlku normalizovanej transformovanej premennej. Software preskúma mnoho transformácii, z ktorých uvdieme iba tie, ktoré sú pre zaokrúhlené hodnoty λ. Y je transformovaná hodnota premennej (nameraného znaku kvality) x

Táto transformácia sa snaží previesť dáta na nové dáta, ktoré sa už dajú popísať normálnym rozdelením. Problémom môže byť fakt, že obdobne ako u Johnsonovej transformácie, síce vhodná transformácia bola nájdená, ale nedá sa transformovať špecifikačné medze, pretože sú mimo definičného oboru transformácie.

Metóda empirických percentilov

V prípade, že nepoznáme rozdelenie pravdepodobnosti sledovaného znaku kvality alebo jeho parametre, alebo sa nedarí vhodné rozdelenie nájsť, potom sa ponúkne približná metóda využitia empirických percentilov vypočítaných z napozorovaných dát. Jedná sa o percentily odpovedajúce percentám, z ktorými pracujú ukazovatele výkonnosti. Aby táto metóda bola aspoň orientačne použiteľná, je treba aby rozsah ozorovaných dát bol dostatočný, najmenej N=100. Problém je v tom, že odhady percentilov, ktoré zodpovedajú malému či veľkému percentu vykazujú značnú variabilitu, alebo sú obvykle závislé od malého počtu najmenších či najväčších hodnôt vo výbere. Tým sú i odhady ukazovateľov výkonnosti zaťažené značnou variabilitou. Táto metóda časti vedie k odhadu referenčného rozmedzia vo forme rozdielu maximálnej a minimálnej hodnoty v napozorovaných dátach sledovaného znaku kvality.

Matematická štatistika pozná celú radu metód pre odhady kvantilov z napozorovaných dát, ale tieto obvykle nie sú súčasťou softwarov pre SPC. Bohužiaľ dosť často tieto metódy vyžadujú stavky dát pre spoľahlivé výpočty konfidenčných intervalov pre kvantily, čo je v mnohých prípadoch v praxi nedosiahnuteľné. Pri vyšetrovaní výkonnosti výrobného procesu u znakov kvality, ktoré sa nedajú popísať normálnym rozdelením, predovšetkým závisí na skúseností pracovníka, ktorý hodnotenie prevádza a na informácii zo skoršieho hodnotenia výrobného procesu. Pretože neexistuje jednoznačné doporučenie ako postupovať, je každý prípad individuálne riešiteľný.

Použitá literatúra

http://library.utia.cas.cz/separaty/2010/SI/michalek-performance%20evaluation%20of%20a%20manufacturing%20process%20by%20non-normally%20distributed%20data.pdf