Kmity sústavy s dvoma stupňami volnosti
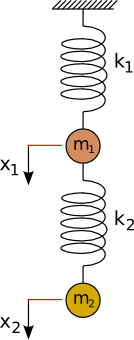
Na obrázku je zobrazená sústava dvoch telies a dvoch pružín. Prvá pružina je pevne ukotvená, hmotnosti telies sú m1 a m2, ich výchylky z rovnovážnej polohy sú x1 a x2. V zobrazenej pozícii je sústava v rovnováhe, pružiny sú natiahnuté pôsobením vlastnej hmotnosti telies, do pohybových rovníc preto nebudeme zahŕňať tiažové sily m1g a m2g.
Pri vychýlení z rovnovážnej polohy pôsobia na telesá sily úmerné ich výchylkám z rovnovážnych polôh a konštantám pružín k1 a k2. Straty energie pri pohybe telies v tomto jednoduchom prípade nebudeme uvažovať. Pre obe telesá môžeme potom napísať pohybové rovnice
- [math] m_1 \ddot{x_1}=-k_1 x_1 + k_2(x_2-x_1) [/math]
- [math] m_2 \ddot{x_2}=-k_2(x_2-x_1) [/math]
Analýza sústavy
Pri analýze sústavy predpokladáme, že pohyb telies bude harmonický s rovnakou frekvenciou a môžeme ho preto popísať vzťahmi
- [math] x_1 =A_1 sin(\omega t)\, [/math]
- [math] x_2 =A_2 sin(\omega t)\, [/math]
Hľadanou veličinou je frekvencia kmitov telies. Dosadením do pohybových rovníc dostaneme
- [math] -m_1 A_1\, \omega^2 + (k_1 + k_2)A_1 - k_2 A_2 = 0\, [/math]
- [math] -m_2 A_2\, \omega^2 - k_2 A_1 + k_2 A_2 = 0\, [/math]
Úpravou dostaneme maticový zápis sústavy pohybových rovníc
- [math] \left[ \begin{array}{cc} {[(k_1+k_2)-m_1 \omega^2]} & -k_2 \\ -k_2 & {[k_2-m_2 \omega^2]} \end{array} \right] \left[ \begin{array}{c} A_1 \\ A_2 \end{array} \right] = 0 [/math]
Homogénna sústava rovníc má netriviálne riešenie len vtedy, ak determinant sústavy je rovný nule, z toho vyplýva
- [math] \omega^4 - \left[ \frac{k_1+k_2} {m_1} + \frac{k_2}{m_2} \right] \omega^2 + \frac{k_1}{m_1} \frac{k_2}{m_2}=0 [/math]
Túto rovnicu nazývame charakteristickou rovnicou systému. Vo všeobecnosti má dva korene [math]\omega_1^2[/math] a [math]\omega_2^2[/math], vlastnými frekvenciami systému potom sú kladné hodnoty [math]\omega_1\,[/math] a [math]\omega_2\,[/math].
Výpočet sústavy
V interaktívnom móde Pythonu (konzola) importujeme balík pylab[1] pre vedecké výpočty. Ak použijeme interaktívny shell iPython[2] [3], balík pylab môžeme automaticky importovať pri spustení shellu
ipython -pylab
Definujeme hmotnosti telies a konštanty pružín
>>> m1=1.0; m2=0.5
>>> k1=500; k2=250
Zostavíme koeficienty charkteristickej rovnice sústavy a nájdeme jej korene
>>> c=[1, -(k1+k2)/m1-k2/m2, k1*k2/(m1*m2)]
>>> z=roots(c)
Vypočítame vlastné frekvencie systému
>>> f=sqrt(z)/(2*pi)
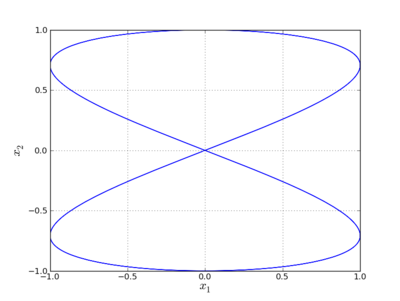
Vlastné frekvencie systému majú hodnoty f[0]=5.03 Hz a f[1]=2.51 Hz. Pre analyzovaný systém môžeme zobraziť jeho fázovú trajektóriu [x1, x2]
>>> t=arange(0.0, 5.0, 0.01)
>>> x1=sin(t*f[0])
>>> x2=sin(t*f[1])
>>> plot(x1,x2)