Java - algoritmy aproximácie
Základy informatiky - jazyk Java
Úvod do programovania v jazyku Java
Java - objektovo orientovaný prístup
Vzorové príklady:
Java - implementácia numerických algoritmov
- >Java - algoritmy hľadania nulových miest
>Java - algoritmy numerického derivovania
>Java - algoritmy numerického integrovania
>Java - algoritmy aproximácie
>Java - algoritmy interpolácie
Java - triedy geometrických tvarov
Pokročilé témy:
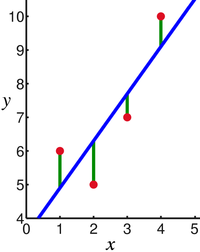
Klasickým problémom vo viacerých vedných disciplínach je nájsť trend vývoja určitej situácie, pričom poznáme len diskrétne hodnoty. Úloha je prostá nájsť takú krivku, ktorá sa najviac približuje daným diskrétnym hodnotám.
Túto úlohu riešia algoritmy aproximácie. Medzi najpoužívanejší algoritmus patrí metóda najmenších štvorcov[1]. Jedná sa o optimalizačný problém, kde je treba nájsť takú krivku (modrá čiara) od ktorej je štvorec vzdialenosti vstupných bodov (červené body) minimálny.
Obsah
Metóda najmenších štvorcov
V praktickom príklade si ukážeme výpočet lineárnej, logaritmickej, exponenciálnej a mocninovej aproximácie. Teória, ktorú budeme potrebovať je v časti Algoritmy numerickej aproximácie (riešené príklady).
Pre úplnosť poznamenajme, že máme k dispozícii n bodov v rovine a cez tieto body chceme preložiť nejakú krivku. Uvedieme len základné tvary hľadaných aproximácií a matematické vyjadrenie riešenia problému.
Lineárna aproximácia
Tvar rovnice hľadanej krivky: [math]y=ax+b\,[/math]
Riešenie:
[math]\begin{align} & a=\frac{n\sum\limits_{i=1}^{n}{{{x}_{i}}{{y}_{i}}}-\sum\limits_{i=1}^{n}{{{x}_{i}}}\sum\limits_{i=1}^{n}{{{y}_{i}}}}{n\sum\limits_{i=1}^{n}{x_{i}^{2}}-{{\left( \sum\limits_{i=1}^{n}{{{x}_{i}}} \right)}^{2}}} \\ & b=\frac{\sum\limits_{i=1}^{n}{{{y}_{i}}}-a\sum\limits_{i=1}^{n}{{{x}_{i}}}}{n} \\ \end{align}[/math]
Logaritmická aproximácia
Tvar rovnice hľadanej krivky: [math]y=a\ln x+b\,[/math]
Riešenie:
[math]\begin{align} & a=\frac{n\sum\limits_{i=1}^{n}{\left( \ln {{x}_{i}} \right){{y}_{i}}}-\sum\limits_{i=1}^{n}{\ln {{x}_{i}}}\sum\limits_{i=1}^{n}{{{y}_{i}}}}{n\sum\limits_{i=1}^{n}{{{\left( \ln {{x}_{i}} \right)}^{2}}}-{{\left( \sum\limits_{i=1}^{n}{\ln {{x}_{i}}} \right)}^{2}}} \\ & b=\frac{\sum\limits_{i=1}^{n}{{{y}_{i}}}-a\sum\limits_{i=1}^{n}{\ln {{x}_{i}}}}{n} \\ \end{align}[/math]
Exponenciálna aproximácia
Tvar rovnice hľadanej krivky: [math]y=b{{e}^{ax}}\,[/math]
Riešenie:
[math]\begin{align} & a=\frac{n\sum\limits_{i=1}^{n}{{{x}_{i}}\ln {{y}_{i}}}-\sum\limits_{i=1}^{n}{{{x}_{i}}}\sum\limits_{i=1}^{n}{\ln {{y}_{i}}}}{n\sum\limits_{i=1}^{n}{x_{i}^{2}}-{{\left( \sum\limits_{i=1}^{n}{{{x}_{i}}} \right)}^{2}}} \\ & B=\frac{\sum\limits_{i=1}^{n}{\ln {{y}_{i}}}-a\sum\limits_{i=1}^{n}{{{x}_{i}}}}{n} \\ \end{align}[/math]
kde [math]B=\ln b[/math].
Mocninová aproximácia
Tvar rovnice hľadanej krivky: [math]y=b{{x}^{a}}\,[/math]
Riešenie:
[math]\begin{align} & a=\frac{n\sum\limits_{i=1}^{n}{\ln {{x}_{i}}\ln {{y}_{i}}}-\sum\limits_{i=1}^{n}{\ln {{x}_{i}}}\sum\limits_{i=1}^{n}{\ln {{y}_{i}}}}{n\sum\limits_{i=1}^{n}{{{\left( \ln {{x}_{i}} \right)}^{2}}}-{{\left( \sum\limits_{i=1}^{n}{\ln {{x}_{i}}} \right)}^{2}}} \\ & B=\frac{\sum\limits_{i=1}^{n}{\ln {{y}_{i}}}-a\sum\limits_{i=1}^{n}{\ln {{x}_{i}}}}{n} \\ \end{align}[/math]
kde [math]B=\ln b[/math].
Riešenie v Jave
Na začiatku bolo povedané že musíme mať niekoľko (min. 2) body podľa ktorých budeme aproximovať. Ako prvý krok si vytvoríme jednoduchú triedu Bod, ktorá bude reprezentovať jeden bod v 2D rovine:
public class Bod {
public double x,y;
public Bod(double x, double y) {
this.x = x;
this.y = y;
}
public Bod() {
this(0,0);
}
}
Trieda obsahuje len konštruktor. Ostatné metódy nie sú potrebné, keďže vnútorné premenné x a y sú verejné.
Vytvorme si novú triedu a nazvime ju Extrapolacia. V tejto triede budeme riešiť algoritmy aproximácie a interpolácie. Naša trieda Extrapolacia musí obsahovať n bodov, ktoré použijeme pri výpočte parametrov aproximovanej krivky. Počet týchto bodov nie je dopredu známy a dokonca sa môže počet behu programu meniť. Pre ukladanie týchto bodov použijeme vstavané rozhranie List[2] (zoznam), resp. triedu ArrayList[3]. Trieda ArrayList dovoľuje vytvoriť zoznam, resp. pole z ľubovoľných objektov. V našom prípade potrebujeme vytvoriť zoznam bodov:
List body<Bod>=new ArrayList<Bod>()
Trieda Extrapolacia bude okrem objektu body ešte obsahovať informáciu type aproximácie, ktorá sa bude počítať (typAproximacie) a parametroch a, b (aproxA, aproxB), ktorá vlastne charakterizujú danú krivku.
import java.util.ArrayList;
import java.util.List;
public class Extrapolacia {
public final static int aproxLin = 0;
public final static int aproxLog = 1;
public final static int aproxExp = 2;
public final static int aproxMoc = 3;
private int typAproximacie;
private double aproxA, aproxB;
public List<Bod> body;
public Extrapolacia() {
body = new ArrayList<Bod>();
this.typAproximacie = Extrapolacia.aproxLin;
}
public void addBod(Bod X) {
body.add(X);
}
public double getA() {
return aproxA;
}
public double getB() {
return aproxB;
}
public int getTypAproximacie() {
return typAproximacie;
}
// ostatne metody triedy Extrapolacia
}
Pre jednoduchšie určovanie typu aproximácie sme si vytvorili statické konštanty aproxLin, aproxLog, aproxExp a aproxMoc. Pri vytváraní objektu Extrapolacia (v konštruktore) sa určí ako prednastavený typ aproximácie lineárna aproximácia.
Metóda addBod pridá do zoznamu bodov body nový bod.
Implementácie metódy najmenších štvorcov
Prvým krokom pri implementácii metódy najmenších štvorcov je vypočítať súčty (sumy) uvedené vo vzorcoch.
Pri lineárnej aproximácie máme súčet x-ových súradníc, súčet y-ových súradníc, súčet štvorca x-vých súradníc a výrazov [math]x_i * y_i[/math]. V programe si označme tieto sumy premennými sx, sy, sxx a sxy.
Pri logaritmickej aproximácii máme naviac súčet logaritmu x-vých súradníc, súčet štvorca logaritmu x-vých súradníc a súčet výrazov [math]ln x_i * y_i[/math]. Označme si tieto sumy premennými slx, slxx a slxy.
Podobne si nazveme aj ostatné sumy. Ak máme všetky tieto sumy vypočítané, môžeme ch dosadiť do výsledného vzorca. Vzorec do ktorého dosadíme tieto sumy bude určený podľa požadovaného typu aproximácie.
Triedu Aproximator doplníme o nasledujúcu metódu:
public void aproximacia(final int typ) {
this.typAproximacie = typ;
double sx = 0, sxx = 0, sy = 0, sxy = 0, slxly = 0;
double slx = 0, slxx = 0, sly = 0, slxy = 0, sxly = 0;
// vypocet sum do vzorcov
for (int i = 0; i < this.body.size(); i++) {
sx += this.body.get(i).x;
slx += Math.log(this.body.get(i).x);
sy += this.body.get(i).y;
sly += Math.log(this.body.get(i).y);
sxy += this.body.get(i).x * this.body.get(i).y;
slxy += Math.log(this.body.get(i).x) * this.body.get(i).y;
sxly += this.body.get(i).x * Math.log(this.body.get(i).y);
slxly += Math.log(this.body.get(i).x) * Math.log(this.body.get(i).y);
sxx += this.body.get(i).x * this.body.get(i).x;
slxx += Math.log(this.body.get(i).x) * Math.log(this.body.get(i).x);
}
int n = this.body.size();
// vysledny vzoroc urcime podla pozadovaneho typu aproximacie
switch (typ) {
case Extrapolacia.aproxLin:
this.aproxA = (n * sxy - sy * sx) / (n * sxx - sx * sx);
this.aproxB = (sy - this.aproxA * sx) / n;
break;
case Extrapolacia.aproxLog:
this.aproxA = (n * slxy - sy * slx) / (n * slxx - slx * slx);
this.aproxB = (sy - this.aproxA * slx) / n;
break;
case Extrapolacia.aproxExp:
this.aproxA = (n * sxly - sly * sx) / (n * sxx - sx * sx);
this.aproxB = (sly - this.aproxA * sx) / n;
this.aproxB = Math.exp(this.aproxB);
break;
case Extrapolacia.aproxMoc:
this.aproxA = (n * slxly - sly * slx) / (n * slxx - slx * slx);
this.aproxB = (sly - this.aproxA * slx) / n;
this.aproxB = Math.exp(this.aproxB);
break;
}
}
V predchádzajúcej metóde boli vypočítané len koeficienty a, b. Do našej aplikácie potrebujeme doplniť ďalšiu metódu, ktorá nám vypočíta funkčnú hodnotu z danej aproximovanej krivky. Do triedy Aproximator doplníme metódu:
public double aproximovanaHodnota(double x) {
double y = 0;
switch (this.typAproximacie) {
case Extrapolacia.aproxLin:
y = this.aproxA * x + this.aproxB;
break;
case Extrapolacia.aproxLog:
y = this.aproxA * Math.log(x) + this.aproxB;
break;
case Extrapolacia.aproxExp:
y = this.aproxB * Math.exp(this.aproxA * x);
break;
case Extrapolacia.aproxMoc:
y = this.aproxB * Math.pow(x, this.aproxA);
break;
}
return y;
}
Použitie metód aproximácie v aplikácii
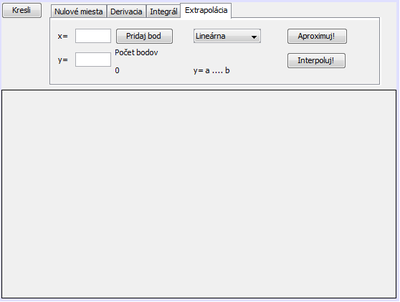
Vo vzorovej aplikácii pridáme na kartu 'Extrapolácia' komponenty podľa nasledujúceho obrázku:
Opis komponentov:
textField
- Dva komponenty textfielt slúžia na zadávanie body (x, y súradnica) do aplikácie
- názov komponentu: textExtraX, textExtraY
label
- Zobrazie počtu bodov pre aproximáciu (na obrázku má hodnotu 0)
- názov komponentu: labelInterpolaciaBody
- Zobrazenie výslednej rovnice proximácie
- názov komponentu: labelRovnica
comboBox
- Výber typu aproximácie - rozbaľovací zoznam
- názov komponentu: comboAproximacia
- Obsahuje 4 položky: Lineárna, Logaritmicá, Exponenciálna a Mocninová.
- Tieto položky nastavíme pomocou vlastnosti model.
button
- Pridanie bodu do zoznamu bodov pre aproximáciu
- text komponentu: 'Pridaj bod'
- názov komponentu: tlcPridajBod
- udalosť tlačidla: tlcPridajBodActionPerformed
- Spustenie aproximácie a vykreslenie výsledku
- text komponentu: 'Aproximuj!'
- názov komponentu: tlcAproximuj
- udalosť tlačidla: tlcAproximujActionPerformed
Obsluha kliknutia tlačidiel:
Udalosť Pridaj bod
private void tlcPridajBodActionPerformed(java.awt.event.ActionEvent evt) {
double x, y;
x = Double.valueOf(textExtraX.getText());
y = Double.valueOf(textExtraY.getText());
e.addBod(new Bod(x, y));
labelInterpolaciaBody.setText(String.valueOf(e.body.size()));
}
Udalosť Aproximuj!
private void tlcAproximujActionPerformed(java.awt.event.ActionEvent evt) {
int i = comboAproximacia.getSelectedIndex();
e.aproximacia(i);
NumberFormat formatter = new DecimalFormat("#0.000");
double a, b;
a = e.getA();
b = e.getB();
// zobrazenie rovnice aproximacie
String rovnica = "y=";
switch (e.getTypAproximacie()) {
case Extrapolacia.aproxLin:
rovnica += formatter.format(a) + "x +" + formatter.format(b);
break;
case Extrapolacia.aproxLog:
rovnica += formatter.format(a) + "ln x +" + formatter.format(b);
break;
case Extrapolacia.aproxExp:
rovnica += formatter.format(b) + "e^(" + formatter.format(a) + "x)";
break;
case Extrapolacia.aproxMoc:
rovnica += formatter.format(b) + "x^" + formatter.format(a);
break;
}
labelRovnica.setText(rovnica); // label s rovnicou aproximacie
//vykreslenie aproximovanej krivky
int sirka, vyska;
sirka = panel.getWidth();
vyska = panel.getHeight();
t.setSize(sirka, vyska);
g = panel.getGraphics();
g.clearRect(1, 1, sirka - 2, vyska - 2);
g.setColor(Color.GRAY);
g.drawLine(0, vyska / 2, sirka, vyska / 2);
g.drawLine(sirka / 2, 0, sirka / 2, vyska);
g.setColor(Color.GREEN);
double x1, y1, x2, y2 = 0;
x1 = -t.getStrana();
y1 = e.aproximovanaHodnota(x1);
for (x2 = -t.getStrana(); x2 < t.getStrana(); x2 += t.getKrok()) {
y2 = e.aproximovanaHodnota(x2);
g.drawLine(t.getX(x1), t.getY(y1), t.getX(x2), t.getY(y2));
x1 = x2;
y1 = y2;
}
// zobrazenie bodov, pre ktore pocitame aproximaciu
int r = 3;
g.setColor(Color.BLACK);
for (Bod A : this.e.body) {
g.drawOval(t.getX(A.x) - r, t.getY(A.y) - r, 2 * r, 2 * r);
}
}
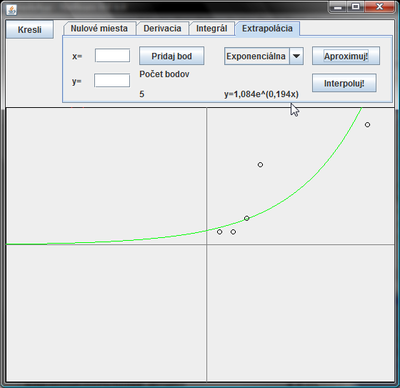
Výsledok: