Java applety - základná práca
Základy informatiky - jazyk Java
Úvod do programovania v jazyku Java
Java - objektovo orientovaný prístup
Vzorové príklady:
- >Java applety - základná práca
>Java applety - interakcia s používateľom
>Java applety - fraktály
>Java applety - animácia
>Java applety - animácie bez blikania
Java - implementácia numerických algoritmov
Java - triedy geometrických tvarov
Pokročilé témy:
Pri práci s grafikou treba pamätať na fakt, že začiatok súradnicového systému [0,0] je v ľavom hornom rohu. Os x rastie smerom doprava a os y rastie smerom dolu.
Kreslenie čiar
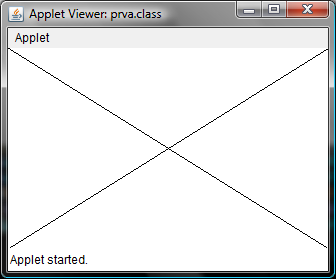
Úloha 1.1: Do appletu nakreslite čiary do oboch uhlopriečok.
Analýza úlohy
Pre kreslenie čiar existuje metóda triedy Graphics drawLine:
public abstract void drawLine(int x1, int y1, int x2, int y2);
Kde:
- x1 - súradnica x prvého bodu.
- y1 - súradnica y prvého bodu.
- x2 - súradnica x druhého bodu.
- y2 - súradnica y druhého bodu.
Súradnica pravého dolného rohu appletu je daná samotnými rozmermi appletu. Teda jeho šírkou a výškou. Tieto hodnoty sa dajú jednoducho zistiť metódami triedy Applet getWidth a getHeight. Body medzi ktorými ideme kresliť čiary sú vlastne rohy okna appletu. Sú to tieto body:
- Ľavý horný roh - [0,0]
- Pravý horný roh - [šírka,0]
- Ľavý dolný roh - [0,výška]
- Pravý dolný roh - [šírka ,výška]
Riešenie:
import java.applet.*;
import java.awt.*;
public class Ciary extends Applet {
public void init() {
}
public void paint( Graphics g ) {
int sirka = this.getWidth();
int vyska = this.getHeight();
g.drawLine(0,0,sirka,vyska);
g.drawLine(0,vyska,sirka,0);
}
}
Výsledok:
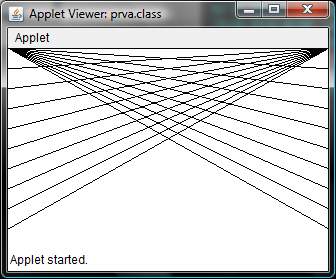
Úloha 1.2: Do prvého appletu doplňte čiary nasledovne: z bodu [0,0] nakreslite "vejár" smerujúci na pravú stranu. Podobne, ale z bodu [sirka,0] nakreslite čiary v tvare vejára na ľavú stranu.
Analýza úlohy V úlohe nie je povedané koľko čiar má mať vejár. Preto si zvoľme n čiar. Toto n potom môžeme ľubovoľne meniť. Keď budeme kresliť čiary z bodu [0,0] na protiľahlú pravú stranu, chceme aby boli rozostupy medzi týmito čiarami rovnaké. Označme si tento rozostup ako krok. Krok vypočítame jednoducho: stačí vydeliť výšku appletu počtom čiar, ktoré chceme nakresliť. Teda: [math]krok=vyska/n[/math]. Postupne budeme kresliť čiary z bodu [0,0] do bodov [sirka,0], [sirka,krok], [sirka,2*krok] ... [sirka,n*krok]. Kde vlastne n*krok je vyska.
Riešenie:
import java.applet.*;
import java.awt.*;
public class Ciary2 extends Applet {
public void init() {
}
public void paint( Graphics g ) {
g.setColor( Color.green );
int sirka = this.getWidth();
int vyska = this.getHeight();
int n=10;
int krok = vyska/n;
for(int i=0; i<n ; i++)
{
g.drawLine(0,0,sirka,i*krok); //vejar zľava doprava
g.drawLine(sirka,0,0,i*krok); //vejar sprava doľava
}
}
}
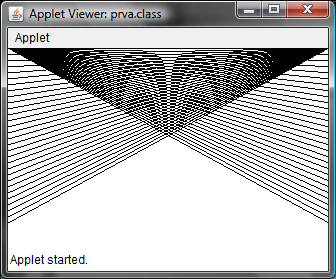
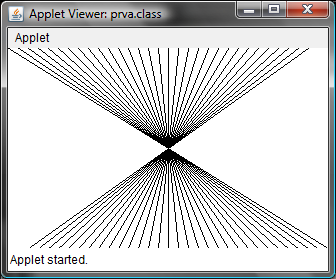
Úloha 1.3: Vytvorte obrazec, z ktorého stredu budú vychádzať čiary k hornému a dolnému okraju okna.
Analýza úlohy
Úlohu si upravíme, aby sa dala ľahšie implementovať. Prvá čiara bude vlastne uhlopriečka okna z ľavého horného rohu do pravého dolného rohu. Teda z bodu [0,0] do bodu [sirka,vyska]. Druhá čiara bude vychádzať z bodu [1*krok,0] do dobu [sirka-1*krok,vyska]. Ďalšia čiara pojde z bodu [2*krok,0] do dobu [sirka-2*krok,vyska]. Posledná čiara pôjde z bodu [n*krok,0] do dobu [sirka-n*krok,vyska]. čo je vlastne [sirka,0] do dobu [0,vyska]. Ešte poznamenajme, že premenná krok je teraz: [math]krok=sirka/n[/math]
Riešenie:
import java.applet.*;
import java.awt.*;
public class Ciary3 extends Applet {
public void init() {
}
public void paint( Graphics g ) {
int sirka = this.getWidth();
int vyska = this.getHeight();
int n=30;
int krok = sirka/n;
for(int i=0; i<=n ; i++)
{
g.drawLine(i*krok,0,sirka-i*krok,vyska);
}
}
}
Výsledok:
Kreslenie ostatných tvarov
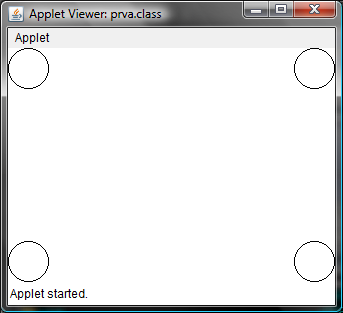
Úloha 2.1: Do všetkých rohov okna appletu nakreslite kruh s polomerom r=20px.
Analýza úlohy
Pre kreslenie kruhu, resp. elipsy existuje metóda triedy Graphics drawOval:
public abstract void drawOval(int x, int y, int width, int height);
Kde:
- x - súradnica x ľavého horného bodu obdĺžnika, v ktorom je v písaná elipsa.
- y - súradnica y ľavého horného bodu obdĺžnika, v ktorom je v písaná elipsa.
- width - Šírka obdĺžnika, v ktorom je v písaná elipsa.
- height - Výška obdĺžnika, v ktorom je v písaná elipsa.
Keďže úlohou bolo nakresliť kruh, šírka a výška obdĺžnika v ktorom je tento kruh bude rovnaká. Konkrétne to bude: 2*r.
- Kruh v ľavom hornom rohu appletu bude mať nasledujúce parametere: bod, v ktorom sa za4ne kresliť: [0,0], šírka=výška=2*r
- Kruh v pravom hornom rohu appletu bude mať nasledujúce parametere: bod, v ktorom sa za4ne kresliť: [šírka-r,0], šírka=výška=2*r
- Kruh v ľavom dolnom rohu appletu bude mať nasledujúce parametere: bod, v ktorom sa za4ne kresliť: [0,výška-r], šírka=výška=2*r
- Kruh v pravom dolnom rohu appletu bude mať nasledujúce parametere: bod, v ktorom sa za4ne kresliť: [šírka-r,výška-r], šírka=výška=2*r
Rišenie:
import java.applet.*;
import java.awt.*;
public class Kruhy extends Applet {
public void init() {
}
public void paint( Graphics g ) {
int sirka = this.getWidth();
int vyska = this.getHeight();
int r=20;
g.drawOval(0, 0, 2*r, 2*r);
g.drawOval(sirka-2*r, 0, 2*r, 2*r);
g.drawOval(0, vyska-2*r, 2*r, 2*r);
g.drawOval(sirka-2*r, vyska-2*r,2*r, 2*r);
}
}
Výsledok:
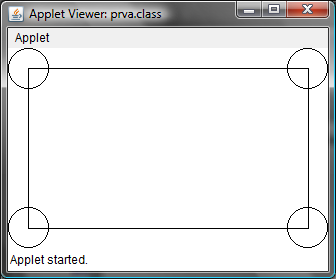
Úloha 2.2: Do appletu doplňte obdĺžnik, ktorého vrcholy budú ležať v stredoch nakreslených kruhov.
Analýza úlohy
Pre kreslenie obdĺžnika, metóda triedy Graphics drawRect:
public void drawRect(int x, int y, int width, int height);
Kde:
- x - súradnica x ľavého horného bodu obdĺžnika
- y - súradnica y ľavého horného bodu obdĺžnika
- width - Šírka obdĺžnika.
- height - Výška obdĺžnika.
Náš obdĺžnik začneme kresliť v bode [r,r]. Šírku obdĺžnika odvodíme od šírky okna appletu. Na ľavej aj na pravej strane sú kruhy vzdialené o vzdialenoť r pixelov od krajov. Preto bude šírka obdĺžnika práve šírka-2*r. Podobne postupujeme aj pri výpočte výšky obdĺžnika.
Rišenie:
import java.applet.*;
import java.awt.*;
public class Kruhy extends Applet {
public void init() {
}
public void paint( Graphics g ) {
int sirka = this.getWidth();
int vyska = this.getHeight();
int r=20;
// vykreslenie kruhv
g.drawOval(0, 0, 2*r, 2*r);
g.drawOval(sirka-2*r, 0, 2*r, 2*r);
g.drawOval(0, vyska-2*r, 2*r, 2*r);
g.drawOval(sirka-2*r, vyska-2*r,2*r, 2*r);
// vykreslenie obdĺžnika
g.drawRect(r,r,sirka-2*r,vyska-2*r);
}
}
Výsledok:
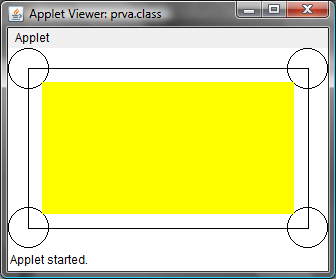
Úloha 2.3: Do appletu doplňte vyplnený obdĺžnik, ktorého vrcholy sa budú dotýkať kruhov, ktoré sú v rohoch.
Analýza úlohy
Pre kreslenie vyplneneého obdĺžnika, metóda triedy Graphics fillRect:
public abstract void fillRect(int x, int y, int width, int height);
Parametre majú rovnaký význam ako v predchádzajúcom príklade. Avšak, obdĺžnik sa vyfarbí aktuálne nastavenou farbou.
Pri kreslení si najskôr treba vypočítať súradnice začiatočného bodu. Náš obdĺžnik sa má dotýkať obvodu kruhu. Jednoduchým výpočtom určíme súradnice x a y:
- x=r+sin(45)*r=1.71*r
- y=r+sin(45)*r=1.71*r
Označme si n=1.71*r
Šírku a výšky určíme jednoducho:
- Šírka obdĺžnika= šírka appletu - n
- Výška obdĺžnika= výška appletu - n
Rišenie:
import java.applet.*;
import java.awt.*;
public class Kruhy extends Applet {
public void init() {
}
public void paint( Graphics g ) {
int sirka = this.getWidth();
int vyska = this.getHeight();
int r=20;
// vykreslenie kruhv
g.drawOval(0, 0, 2*r, 2*r);
g.drawOval(sirka-2*r, 0, 2*r, 2*r);
g.drawOval(0, vyska-2*r, 2*r, 2*r);
g.drawOval(sirka-2*r, vyska-2*r,2*r, 2*r);
// vykreslenie obdĺžnika
g.drawRect(r,r,sirka-2*r,vyska-2*r);
// vykreslenie vyplneného obdĺžnika
g.setColor(Color.yellow);
int n=(int)(1.71*r);
g.fillRect(n,n,sirka-2*n,vyska-2*n);
}
}
Farby
V nasledujúcej časti budeme pracovať s farbami. Rozlišujeme farbu pozadia a farbu, ktorá sa použije pre vykresľovanie grafiky. Pre zmenu farby vykresľovania existuje metóda setColor:
public abstract void setColor(Color c);
Parametrom metódy setColor musí byť objekt triedy Color. Trieda Color obsahuje statické objekty typu Color. Môžeme teda uvieť priamo názov farby v tvare:
setColor(Color.red);
//alebo veľkými písmenami
setColor(Color.RED);
V triede Color sú definované nasledujúce farby:
- black
- blue
- cyan
- darkGray
- gray
- green
- lightGray
- magenta
- orange
- pink
- white
- yellow
Farbu môžeme definovať aj pomerným zastúpením jej farebných zložiek RGB, teda červená-zelená-modrá nasledovne:
- Color(float r, float g, float b), kde r, g, b sú hodnoty on 0 po 1
- Color(float r, float g, float b, float alfa), kde r, g, b majú rovnaký význam a alfa je alfa-kanál (priehľadnosť)
- Color(int r, int g, int b), r, g, b sú celočíselné hodnoty v intervale 0-255.
- Color(int r, int g, int b, int a)kde r, g, b majú rovnaký význam a alfa je alfa-kanál (priehľadnosť)
Farba pozadia (background) sa dá nastaviť pomocou metódy setBackground triedy Component. Keďže aj trieda Applet je potomkom triedy Component, metóda setBackground sa dá použiť aj pre nastavenia pozadia appletu.
public void setBackground(Color c)
V príklade budeme pracovať s textom. Text sa v applete dá nakresliť pomocou metódy drawString. Definícia tento metódy je nasledovná:
drawString(String str, int x, int y)
Kde str je reťazec, ktorý sa vykreslí na pozíciu [x, y]. Bod definovaný súradnicou [x,y] je bod začiatku riadku (ľavý dolný roh).
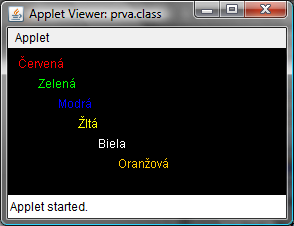
Úloha 3.1: Do appletu vpíšte názvy všetkých základných farieb. Farba písma bude rovnaká ako názov farby.
import java.applet.*;
import java.awt.*;
public class prva extends Applet {
public void init() {
}
public void paint( Graphics g ) {
setBackground(Color.black);
g.setColor(Color.red);
g.drawString("Červená",10,20);
g.setColor(Color.green);
g.drawString("Zelená",30,40);
g.setColor(Color.blue);
g.drawString("Modrá",50,60);
g.setColor(Color.yellow);
g.drawString("Žltá",70,80);
g.setColor(Color.white);
g.drawString("Biela",90,100);
g.setColor(Color.orange);
g.drawString("Oranžová",110,120);
}
}
Výsledok:
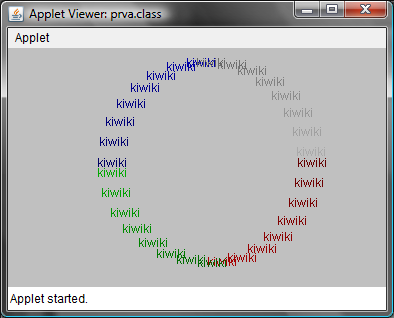
Úloha 3.2: Do appletu vpíšte text "kiwiki". Text bude v kruhu s polomerom r. Farba textu sa bude meniť nasledovne:
- v prvej štvrtine kruhu bude v odtieňoch červenej
- v druhej štvrtine kruhu bude v odtieňoch zelenej
- v tretej štvrtine kruhu bude v odtieňoch modrej
- v poslednej štvrtine kruhu bude v odtieňoch šedej
Analýza úlohy:
Text bude umiestnený v kruhu so stredom v strede okna appletu. Kruh má mať polomer r. Z toho si jednoducho vypočítame vzdialenosť od stredu okna, kde sa má začať vypisovať text:
- Stred okna je: [stredX , stredY], kde
- stredX = this.getWidth()/2;
- stredY = this.getHeight()/2;
- vzdialenosť vypisovaného textu od stredu [stredX , stredY] je r. Súradnice, kde budeme text vypisovať si označme [x,y]:
- x = r * cos(alfa) + stredX;
- y = r * sin(alfa) + stredY;
- Kde alfa je ohol posunutia
Určenie farby:
Farbu budeme zadávať pomocou vytvorenia nového objektu typu Color s určením zastúpenia farebných zložiek. Pre červenú farbu budeme meniť prvý parameter pri výtváraní objektu Color, pri modrej farbe druhý a pri zelenej farbe tretí parameter. Odtiene šedej dostaneme tak, že budeme súčasne meniť všetky tri parametre v kanštruktore Color tak, aby mali rovnaké hodnoty. Povolený interval pri definovaní farieb je 0-255. Aby bolo lepšie vidieť zmeny, budeme tento parmater meniť od 100 do 255. V príklade je to premenná i. Krok zmeny farby je definovaný ako 155/n, kde n je konštanta.
Vykresľovanie do kruhu:
Knižnica Math počíta s uhlami uvedenými v oblúkovej miere, teda v radiánoch. Kruh má 2*PI radiánov. Preto sa pri vykresľovaní mení parameter alfa postupne (0,PI/2), (PI/2,PI), (PI,3/2*PI), (3/2*PI, 2*PI). Krok zmeny je definovaný ako PI/n, kde n je konštanta.
Riešenie:
import java.applet.*;
import java.awt.*;
public class prva extends Applet {
public void init() {
}
public void paint( Graphics g ) {
int stredX = this.getWidth()/2;
int stredY = this.getHeight()/2;
int r=100;
double x,y;
setBackground(Color.lightGray);
int n=15;
int zmenaFarby=155/n;
int i=100;
double alfa;
// prvá štvrtina - odtiene červenej
for(alfa=0;alfa<Math.PI/2;alfa+=Math.PI/n,i+=zmenaFarby)
{
x=r*Math.cos(alfa)+stredX;
y=r*Math.sin(alfa)+stredY;
g.setColor(new Color(i,0,0));
g.drawString("kiwiki",(int)x,(int)y);
}
// druhá štvrtina - odtiene zelenej
for(i=100,alfa=Math.PI/2;alfa<Math.PI;alfa+=Math.PI/n,i+=zmenaFarby)
{
x=r*Math.cos(alfa)+stredX;
y=r*Math.sin(alfa)+stredY;
g.setColor(new Color(0,i,0));
g.drawString("kiwiki",(int)x,(int)y);
}
// tretia štvrtina - odtiene modrej
for(i=100,alfa=Math.PI;alfa<Math.PI*1.5;alfa+=Math.PI/n,i+=zmenaFarby)
{
x=r*Math.cos(alfa)+stredX;
y=r*Math.sin(alfa)+stredY;
g.setColor(new Color(0,0,i));
g.drawString("kiwiki",(int)x,(int)y);
}
// posledná štvrtina - odtiene sivej
for(i=100,alfa=Math.PI*1.5;alfa<Math.PI*2;alfa+=Math.PI/n,i+=zmenaFarby)
{
x=r*Math.cos(alfa)+stredX;
y=r*Math.sin(alfa)+stredY;
g.setColor(new Color(i,i,i));
g.drawString("kiwiki",(int)x,(int)y);
}
}
}
Iné zaujímavé útvary
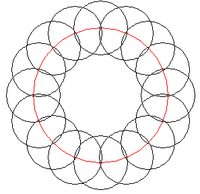
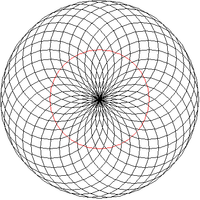
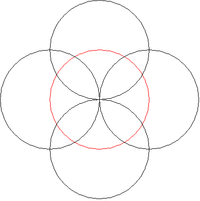
Sústredené kružnice: Vytvorte obrazec skladajúci sa z kruhov, ktorých stredy ležia inej kružnici.
Analýza:
V úlohe máme jednu "väčšiu" kružnicu K, ktorá slúži ako určitá šablóna pri vykresľovaní všetkých ostatných kružníc. Všetky ostatné kružnice budú mať svoj stred práve na tejto kružnici K. Kružnica K bude mať sted v bode [X,Y] a polomer bude mať R (bude vykreslená na červeno).
Pre body [x,y], ktoré ležia obvode kružnice platí: [math]f(x)=\sqrt{x^2+y^2}[/math]
Ak stred kruhu leží v bode [X,Y], tak sa rovnica zmení na: [math]f(x)=\sqrt{(x+X)^2+(y+Y)^2}[/math]
Stredy kružníc, ktoré máme vykresliť spĺňať predchádzajúcu podmienku. Úlohe je teda určiť stedy týchto kružníc. Ak predchádzajúci vzťah zapíšeme pomocou parametrov R a [math]\alpha[/math]:
[math]x=R*\cos{\alpha}\![/math]
[math]y=R*\sin{\alpha}\![/math]
respektíve, ak uvažujeme, že kružnica R má sted v bode [X, Y]:
[math]x-X=R*\cos{\alpha}\![/math]
[math]y-Y=R*\sin{\alpha}\![/math]
teda:
[math]x=R*\cos{\alpha}+X\![/math]
[math]y=R*\sin{\alpha}+Y\![/math]
Riešenie:
Podľa predchádzajúcej matematickej analýzy, budú stedy kružníc nasledovné:
[math][R*\cos{\alpha}+X,R*\sin{\alpha}+Y]\![/math]
V tomto vzťahu stačí meniť len hodnotu uhla [math]\alpha\![/math]. V applete budeme postupne vykreľovať kruhy, začneme od uhla 0 a skončíme pri uhle 360°, resp. 2*PI radiánov. Po vykreslení kruhu sa posunieme o hodnotu krok (radiánov).
Poznámka: Pri riešení využijeme triedu Kruh, definovanú v Java - triedy geometrických tvarov.
public class kruhy extends Applet {
Kruh k,K;
public void init() {
k=new Kruh(10,10,10);
K=new Kruh(10,10,10);
}
public void paint(Graphics g)
{
k.setR(40); // nastavenie polomeru malych kruznic
double alfa;
int x,y; // pomocne premenne: stred 'maleho' kruhu
// velka kruznica
K.setBod(200, 200);
K.setR(100);
g.setColor(Color.red); // farba vykreslovania velkej kruznice
// velka kruznica
g.drawOval(K.getX(), K.getY(), K.getRozmer(), K.getRozmer());
// farba vykreslovania malych kruznic
g.setColor(Color.black);
double krok=Math.PI/8;
for (alfa = 0; alfa < 2*Math.PI; alfa+=krok) {
x=(int)(R*Math.cos(alfa))+X;
y=(int)(R*Math.sin(alfa))+Y;
k.setBod(x,y); // nova pozicia malej kruznice
g.drawOval(k.getX(), k.getY(), k.getRozmer(), k.getRozmer());
}
}
}
Pre všetky obrázky platí K: [200,200], R=100
Kde K červená kružnica, r je polomer čiernych kružníc, a krok je inkrement v uhle alfa.