Teória grafov
Obsah
Teória grafov
V matematike a počítačových vedách sa teória grafov zaoberá štúdiom grafov, teda grafických matematických štruktúr používaných na modelovanie vzájomných vzťahov medzi objektami z určitej množiny. Teória grafov je súčasťou diskrétnej matematiky.
Základné pojmy a charakteristika grafov
V matematike sa pojem graf používa najčastejšie v zmysle grafického znázornenia určitej funkcie , napr. y=f(2x+3). Grafy, ktoré sú objektom štúdia teórie grafov sú však svojou povahou veľmi vzdialené od grafov funkcií. Sú to objekty tvorené určitou množinou bodov a čiar, ktoré tieto body spájajú na základe určitých pravidiel. Graf môžu tvoriť napr. mestá pospájané železnicou, rôzne miesta prepojené mostami ale aj elektrické siete alebo chemické zlúčeniny.
K tomu, aby bol zadaný graf (označíme ho φ) je treba, aby boli dané dve množiny: množina vrcholov V (predtým zmieňované body v grafe) a množina hrán H (zmienené čiary). Vo väčšine prípadov sú obe množiny konečné, avšak nie je to nutná podmienka existencie grafu. Graf potom zapisujeme ako φ=VH, prípadne φ=(V,H).
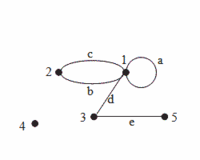
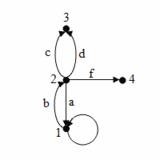
Ku každej hrane musia patriť dva vrcholy, ktoré sú touto hranou spojené a nazývajú sa krajné vrcholy hrany. Hovoríme aj, že krajné vrcholy ležia na spoločnej hrane. Vrcholy sa nazývajú susednými ak existuje taká hrana, na ktorej oba vrcholy ležia. Môže však existovať aj vrchol, ktorý nepatrí k žiadnej hrane. V takomto prípade hovoríme o izolovanom vrchole. K tomu, aby z množín vrcholov a uzlov mohol vzniknúť graf je ďalej potrebné poznať pravidlo, na základe ktorého vieme určiť, ktoré dvojice vrcholov majú byť spojené hranou. Jednotlivé hrany môžu tiež určovať smer vzájomnej interakcie krajných vrcholov. Vtedy hovoríme o orientovanej hrane a označujeme ju šípkou. Graf, ktorý obsahuje len orientované hrany sa nazýva orientovaný graf. Ak sú v grafe orientované aj neorientované hrany, ide o zmiešaný graf. Krajné vrcholy pri orientovaných hranách sú potom nazvané počiatočný a koncový vrchol hrany. Slučku v grafe tvorí hrana, ktorej krajné vrcholy splývajú (sú tvorené jedným vrcholom). Priľahlé hrany sú také, ktoré majú aspoň jeden spoločný krajný vrchol. Dve navzájom rôzne hrany, ktoré majú rovnaké krajné vrcholy sa v neorientovanom grafe nazývajú rovnobežné. V orientovanom grafe potom takéto hrany rozlišujeme podľa orientácie na súhlasne rovnobežné a nesúhlasne rovnobežné. Neorientovaný graf je jednoduchý ak v ňom neexistujú žiadne rovnobežné hrany.[1]
Základné druhy grafových štruktúr
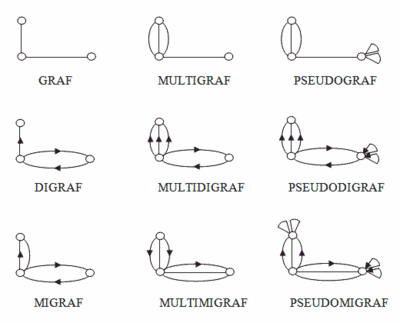
Najvšeobecnejšiu grafovú štruktúru predstavuje pseudomigraf. Od tohto typu grafu sa potom postupnými obmedzeniami dajú získať všetky podskupiny. Dôležitú úlohu pri určovaní typu grafovej štruktúry hrá násobná hrana. Rovnobežné hrany sa nazývajú násobné ak sú všetky neorientované alebo ak sú všetky orientované a majú rovnakú orientáciu. Rôzne druhy grafov sú znázornené na obr. 5. Počet hrán, ktoré vychádzajú z jedného vrcholu sa označuje aj ako stupeň vrcholu.
Graf neobsahuje orientované hrany, slučky ani násobné hrany. Takýto graf sa nazýva aj jednoduchý graf. Multigraf neobsahuje orientované hrany a slučky. Pseudograf neobsahuje orientované hrany.
Digraf (z angl. digraph = directed graph, v prekl. orientovaný graf) neobsahuje neorientované hrany, slučky a násobné hrany (rôzne orientované rovnobežné hrany obsahovať môže). Multidigraf neobsahuje neorientované hrany a slučky. Pseudodigraf neobsahuje len neorientované hrany.
Migraf (z angl. mixed graph, v prekl. zmiešaný graf) neobsahuje násobné hrany a slučky. Multimigraf neobsahuje slučky. Pseudomigraf môže obsahovať všetky druhy hrán.[2]
Každý z týchto typov grafových štruktúr môže mať k prvkom svojej štruktúry priradenú určitú hodnotu (váhu), ktorá reprezentuje výhodnosť prechodu daným prvkom. Takýto graf potom nazývame ohodnotený alebo vážený graf. Rozoznávame hranovo ohodnotený graf a vrcholovo ohodnotený graf. Ohodnotené hrany môžu napr. reprezentovať vzdialenosti medzi miestami, ktoré predstavujú jednotlivé vrcholy. Ohodnotené môžu byť hrany aj vrcholy zároveň a to aj viacerými hodnotami, kde každá hodnota predstavuje inú veličinu (napr. vzdialenosť, čas, cenu, atď). Pomocou takto ohodnotených grafov sa dá reprezentovať a riešiť množstvo praktických problémov, z ktorých najvýznamnejšie sú rozpísané v nasledujúcej kapitole.
Typy problémov riešených pomocou teórie grafov
Štúdiom a hľadaním riešení problémov reprezentovaných rôznymi typmi grafov sa zaoberá teória grafov. História teórie grafov je hlavne oproti iným oblastiam matematiky pomerne krátka. Prvé zmienky o úlohách vyjadrených grafmi súviseli s rôznymi hlavolamami a za skutočný počiatok teórie grafov sa považuje až riešenie hlavolamu známeho pod názvom Problém Kaliningradských mostov (vtedajší Königsberg, v preklade Kráľovec), ktoré publikoval významný matematik Leonhard Euler v roku 1736. Prvú knihu o teórii grafov však napísal až v roku 1936 Dénes König. Odvtedy sa toto odvetvie matematiky výrazne rozvíja a nachádza uplatnenie v rôznych oblastiach ľudskej činnosti.
Hľadanie subgrafov (podgrafov)
Podgraf tvorí v teórii grafov podmnožinu určitého grafu. Podgraf vznikne vylúčením niektorých vrcholov z množiny grafu a zároveň vylúčením hrán, ktoré spájali tieto odstránené vrcholy. V takom prípade sa jedná o indukovaný podgraf. Vylúčený môže byť navyše aj ľubovoľný počet hrán. Ak množina vrcholov podgrafu H je zhodná s množinou vrcholov grafu G, V(H)=V(G), potom hovoríme, že podgraf H je faktorom grafu G. Kostrou grafu nazývame taký faktor grafu, ktorý neobsahuje tzv. kružnice. Kružnicou je taký graf, ktorý je tvorený uzavretou postupnosťou prepojených vrcholov. Kružnica môže byť orientovaná alebo neorientovaná. Graf, ktorý ako podgraf obsahuje kružnicu je označovaný ako cyklický. V opačnom prípade sa jedná o acyklický graf (strom).
Jedným z najznámejších aloritmov na hľadanie podgrafov je napr. Primov algoritmus na hľadanie minimálnej kostry grafu.
Farbenie grafov
Farbenie grafov je špeciálnym prípadom označovania prvkov grafov. Rozlišujú sa tri druhy farbenia grafov. Pri farbení vrcholov sa vrcholy značia takou farbou, aby žiadne dva vrcholy spojené spoločnou hranou nemali rovnakú farbu. Pri farbení hrán nesmú mať rovnakú farbu zase hrany, ktoré spájajú rovnaký vrchol. Poslednou možnosťou je farbenie plôch, ktorých hranice sú v planárnom grafe určené hranami. Planárny (rovinný) graf je taký, kde sa nepretínajú žiadne hrany. Oba problémy farbenia hrán a plôch môžu byť prevedené na farbenie vrcholov.[3]
Problémy s farbením grafov sa vyskytli v 19. storočí pri vyfarbovaní štátov na mapách. Bolo treba určiť minimálny potrebný počet farieb, ktoré zabezpečia, že žiadne dva susediace štáty nebudú rovnakej farby. Populárnou aplikáciou farbenia grafov je napr. hra sudoku.
Hľadanie cesty
Úlohy s hľadaním určitej cesty v grafoch sú pravdepodobne najstaršími úlohami v teórii grafov vôbec a aj dodnes najviac problémov riešených pomocou grafov súvisí s hľadaním určitej optimálnej cesty. Ako príklad možno uviesť problém Kaliningradských mostov, ktorý vyriešil Euler.
Cez Kaliningrad tečie rieka Pregoľa (vtedajšia Pregel), ktorá vytvára dva ostrovy a tým rozdeľuje mesto na štyri časti. Jednotlivé časti boli pospájané siedmimi mostami ako je to znázornené na obr. 11. Úloha hlavolamu spočívala v navrhnutí cesty, ktorá by viedla cez všetky mosty, ale po každom moste sa smie prejsť len raz. Euler dokázal, že riešenie takúto cestu nájsť nie je možné. Hneď na začiatku si uvedomil, že trasa akou sa prechádza po danej časti mesta je irelevantná a záleží len na tom v akom poradí sa počas cesty bude prechádzať cez jednotlivé mosty. Štyri časti mesta teda znázornil len jednoduchými bodmi, ktoré potom poprepájal čiarami predstavujúcimi mosty ako je to ukázané na obr. 9. Tým sa aj zároveň ukazuje, že interpretácia problémov pomocou grafov nezávisí od mnohých vlastností skutočných objektov. V tomto prípade sa napr. neberie do úvahy vzdialenosť mostov, tvar prejdenej trasy, tvar rieky, ani tvar častí mesta.
Euler potom poukázal na to, že aby bolo možné prejsť nejakým vrcholom (pevninou) bez toho, aby po jednej hrane (most) neprešlo viackrát je potrebné, aby daný vrchol obsahoval aspoň dve hrany. Jednu hranu treba na vstup do vrcholu a druhú na výstup. To znamená, že na to, aby sa dalo prejsť všetkými hranami spojenými s daným vrcholom, musí byť daný vrchol párneho stupňa (mať párny počet hrán). To však nemusí platiť pre vstupný a výstupný vrchol, pretože z týchto dvoch vrcholov sa nemusíme ďalej presúvať. Daný graf má štyri vrcholy, kde dva môžeme považovať za vstupné a výstupné. Pre tieto platí, že môžu obsahovať aj nepárny počet hrán. No ďalšie dva vrcholy musia už byť párneho stupňa, pretože sa na nich vstúpi a musí sa z nich dať aj vystúpiť. Keďže všetky vrcholy v danej úlohe sú nepárneho stupňa (stupeň vrchola a je 5, ostatné majú stupeň 3), úloha je neriešiteľná.
Postupnosť vrcholov a hrán, ktorými prechádzame v grafe sa nazýva sled. Počet hrán, ktorými v danom slede prejdeme označujeme ako dĺžka sledu. V teórii grafom sa často riešia problémy hľadania určitej cesty alebo ťahu. Cesta je sled, v ktorom sa vrcholmi v slede prechádza iba raz. Pri ťahu sa zase v slede neprechádza viackrát po hranách. Frekventovanými sú napríklad úlohy, pri ktorých treba nájsť kružnicu, ktorá prechádza všetkými vrcholmi grafu. Jedná sa o tzv. Hamiltonovskú cestu, ktorá je pomenovaná podľa Williama Rovana Hamiltona, ktorý vynašiel tzv. Icosianskú hru, dnes známu aj ako Hamiltonov hlavolam. Hamiltonovská cesta aplikovaná na hranovo ohodnotené grafy je známa ako problém obchodného cestujúceho. V tomto probléme má obchodný cestujúci navštíviť n miest, ale precestovať pritom najkratšiu vzdialenosť. Podobným typom je tzv. Eulerovský ťah, kde je potrebné nájsť sled, pri ktorom sa prejde všetkými hranami práve raz. Toto je aj prípadom problému siedmych Kaliningradských mostov.
Vyhľadávanie optimálneho sledu v grafoch súvisí s mnohými praktickými problémami od hľadania vhodnej cesty pre kropiace auto, určovanie trasy doručovania pošty až po určovanie trasy v GPS navigáciách alebo v robotike.
Sieť toku
Sieť toku je orientovaný graf, v ktorom každá hrana má svoju kapacitu a do každej hrany prúdi tok. Množstvo toku danou hranou nesmie prekročiť jej kapacitu. Pre každý vrchol, okrem zdroja toku a odvodu toku, musí platiť, že množstvo “pritekajúceho“ toku do vrcholu je rovné množstvu “odtekajúceho“ toku z vrcholu.[4] Tento druh grafov sa využíva na modelovanie premávky v dopravnom systéme, tekutín v potrubí, prúdu v elektrických sieťach a iných praktických aplikáciách.
Rozhodovacie stromy
Rozhodovací strom je druhom orientovaného grafu, ktorý neobsahuje žiadne kružnice. V počiatočnom vrchole takéhoto grafu nekončí žiadna hrana a v ostatných vrcholoch končí vždy práve jedna hrana. Každý vrchol, okrem posledných - listových vrcholov, predstavuje určitú rozhodovaciu situáciu. Po rozhodnutí vo vrchole vedie postup cez hranu, ktorá zodpovedá danému rozhodnutiu v počiatočnom vrchole. Takto sa pokračuje až do koncového vrcholu, ktorý reprezentuje výsledný stav ovplyvnený rozhodnutiami v jednotlivých vrcholoch rozhodovacieho stromu.
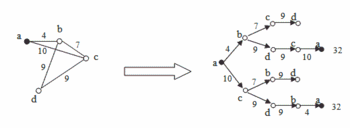
Obrázok 10 znázorňuje interpretáciu riešenia problému obchodného cestujúceho pomocou rozhodovacieho stromu. V každom vrchole stromu sa obchodný cestujúci rozhoduje, ktorým mestom sa môže ďalej vydať. Jednotlivé hrany sú ohodnotené vzdialenosťou, ktorú musí prejsť. V danom prípade má úloha dve riešenia, kde cesta obchodného cestujúceho bude mať dĺžku 32.
Cieľom rozhodovacích stromov je rozdeliť alebo charakterizovať určité objekty do podkategórií podľa určitých vlastností. Prvý uzol by mal obsahovať najvšeobecnejšiu charakteristiku skúmaných objektov, v ďalších by sa postupne mali vlastnosti objektu postupne viac a viac upresňovať až pokiaľ sa nedôjde k poslednému vrcholu. Vtedy je už objekt daný na vstupe pomerne presne charakterizovaný (za predpokladu správnych podmienok v jednotlivých vrcholoch). Príkladom použitia rozhodovacích stromov môžu byť aj herné stromy.
Odkazy
- ↑ Nečas, Jiří. Grafy a jejich použití. Praha : SNTL, 1978.
- ↑ Plesník, Ján. Grafové algoritmy. Bratislava : VEDA, 1983.
- ↑ Graph coloring. Wikipedia. [Online] 2008. [Dátum: 2. 1 2009.] http://en.wikipedia.org/wiki/Graph_coloring.
- ↑ Flow network. Wikipedia. [Online] 2009. [Dátum: 2. 1 2009.] http://en.wikipedia.org/wiki/Network_flow.