Prehľadávanie do šírky

Algoritmy a programovanie

---

Dátový typ

Štruktúry

Rekurzia

Algoritmy vyhľadávania

Algoritmy triedenia

Lineárny zoznam

Binárny strom

Numerické algoritmy

Grafové algoritmy

>Prehľadávanie do šírky
>Prehľadávanie do hĺbky
>Hľadanie najkratšej cesty

Prehľadávanie do šírky (anglicky Breadth-first search - BFS) je grafový algoritmus, ktorý postupne prechádza všetky vrcholy v danej komponente súvislosti. Algoritmus najprv prejde všetkých susedov začiatočného vrcholu, potom susedov týchto susedov atď. až pokiaľ neprejde celú komponentu súvislosti.

Princíp algoritmu

Principiálny algoritmus sa skladá z nasledujúcich krokov :

• v grafe začíname od určitého, stanoveného vrcholu,
• postupne spracujeme všetky susedné vrcholy, ktoré sú s počiatočným vrcholom spojené hranou (majú vzdialenosť 1 hrana),
• až potom z týchto vrcholov navštívime ďalšie susediace a nespracované vrcholy (tie sú už od počiatočného vrcholu vzdialené o dve hrany), potom vrcholy vzdialené o 3 hrany, atď.
• aby sme rozlíšili tie vrcholy, ktoré sme už navštívili a zbytočne ich opätovne nespracovávali, použijeme stavovú položku IsVisited v každom vrchole:
  • na začiatku zabezpečíme, aby mali všetky vrcholy nastavenú položku IsVisited na hodnotu false,
  • postupne, ako budeme vrcholy navštevovať, budeme týmto vrcholom nastavovať IsVisited na hodnotu true,
• prechádzanie do šírky vyzerá tak, akoby sa od počiatočného vrcholu grafom šírila vlna do vzdialenejších a vzdialenejších vrcholov .

Aplikácie algoritmu BFS

• Hľadanie všetkých uzlov v jednom súvislom komponente grafu,
• Cheney-ho algoritmus,
• hľadanie najkratšej cesty medzi dvoma vrcholmi ,
• testovanie grafu na bipartitnosť.

Implementácia algoritmu BSF

Preudokód

1. Označkujeme iba vrchol r.
   • VZDIALENOST(r)=0.
   • Do zoznamu Q typu LIFO dáme r.
2. Ak je Q prázdna, tak koniec
3. Z fronty Q zoberieme vrchol a označíme ho v.
4. Pre každého následníka w vrcholu v (ktorý nie je označkovaný) priradíme:
   1. VZDIALENOST(w)=VZDIALENOST(v)+1
   2. Označkujeme w
   3. Pripíšeme w na koniec zoznamu Q
5. Choď na krok 2

Ukážka k predchádzajúcemu pseudokódu:

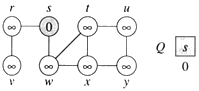
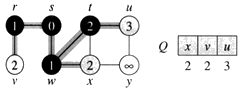
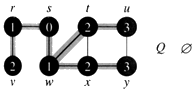
Máme graf s vrcholmi V={r,s,t,u,v,w,x,y} a hranami E={(v,r),(r,s),(s,w),(w,t),(w,x),(t,u),(t,x),(u,y),(x,y) }

• Graf začneme prehšadávať vo vrchole s. Krok 1: označkujeme si vrchol s: VZDIALENOST(s)=0, do zoznamu pridáme vrchol s: Q=[s]

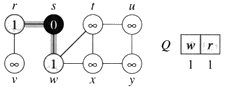
• Krok 3 a 4: Z fronty Q odoberieme vrchol s a vložíme tam všetky vrcholy, ktoré sú susedmi vrcholu s a ešte nie sú označkované. Vzdialenosť od vrchola s je zapísaná vo vrchole.
  • Q=[w,r]
  • VZDIALENOST[w]=1, VZDIALENOST[r]=1.

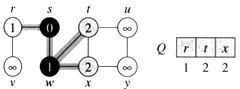
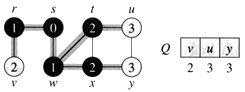
• Z fronty Q odoberieme vrchol w a vložíme tam neoznačkovaných susedov vrcholu w (vrcholy t, x):
  • Q=[r,t,x]
  • VZDIALENOST[t]=2, VZDIALENOST[x]=2.

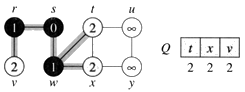
• Z fronty Q odoberieme vrchol r a vložíme tam neoznačkovaných susedov vrcholu r (vrchol v):
  • Q=[t,x,v]
  • VZDIALENOST[v]=2.

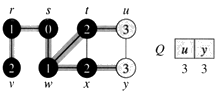
• Z fronty Q odoberieme vrchol t a vložíme tam neoznačkovaných susedov vrcholu t (vrchol u):
  • Q=[x,v,u]
  • VZDIALENOST[u]=3.

• Z fronty Q odoberieme vrchol x a vložíme tam neoznačkovaných susedov vrcholu x (vrchol y):
  • Q=[v,u,y]
  • VZDIALENOST[y]=3.

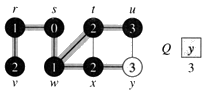
• Z fronty Q odoberieme vrchol v. Pre vrchol v neexistujú také susedné vrcholy, ktoré ešte neboli označkované.
  • Q=[u,y]

• Z fronty Q odoberieme vrchol u. Pre vrchol u neexistujú také susedné vrcholy, ktoré ešte neboli označkované.
  • Q=[y]

• Z fronty Q odoberieme vrchol y. Pre vrchol y neexistujú také susedné vrcholy, ktoré ešte neboli označkované.
  • Q=[]

• Koniec

Kód v jazyku C

Algoritmus prehľadávania do šírky naprogramujeme pomocou radu. Graf budeme reprezentovať pomocou matice susednosti vrcholov (pozri Grafové algoritmy). Nech sú vrcholy označené malými písmenami abecedy (a,b,c,d,...z). Prvý vrchol nech je označený 'a', druhý 'b' atď. Matica reprezentucúja graf bude celočíselná matica, kde riadok č. 0 reprezentuje prvý vrchol, čiže vrchol 'a'.

Opis funkčného prototypu:

int **graf:maticová reprezentácia grafu.

int pv: počet vrcholov grafu graf.

int r: požiatočný vrchol

int vzdialenost[]: pole vzdialeností od vrcholu r

 1 void bfs(int **graf, int pv, int r, int vzdialenost[])
 2 {   int v,i,j;
 3     int *oznackovane;
 4     oznackovane=new int[pv+1];
 5     for(int i=0;i<pv;i++)
 6     {
 7       vzdialenost[i]=10000;
 8       oznackovane[i]=0;
 9     }
10     FIFO fronta;
11     fronta.hlava=fronta.chvost=0;
12     push(fronta,r-'a');
13     oznackovane[r-'a']=1;
14     while(!jePrazdne(fronta))
15     {
16        v=pop(fronta);      
17        for(i=0;i<pv;i++)
18        {
19           if(graf[v][i]==1 && oznackovane[i]==0)
20           {  vzdialenost[i]=vzdialenost[v]+1;
21              oznackovane[i]=1;
22              push(fronta,i);
23           }
24        }            
25     }      
26 }

Komentáre ku zdrojovému kódu

• Riadok 3-4: oznackovane - pole v ktorom bude zoznam označkovaných vrhcolov. Ak oznackovane[i]=1, tak je vrhcol i označkovaný.
• Riadok 7-8: Na začiatku sú všetky vrcholy neoznačkované a vzdialenosť z vrcholu r je nekonečno (resp. veľmi veľká vzdialenosť).
• Riadok 10: Fronta, do ktorej budú ukladané vrcholy, cez ktoré sme prešli. Dátová štruktúra fronta je opísaná v časti FIFO.
• Riadok 12: Vrcholy sú označené písmenami ('a', 'b', ...), ale vnútorná reprezentácia vrcholov sú čísla (0,1,...). Preto pri vkladaní vrcholu r do fronty vložíme poradie vrcholu grafu graf.
• Riadok 13: Vrchol r si označíme ako označkovaný.
• Riadok 15-25: Opakujeme cyklus, pokiaľ sú vo fronte nejaké vrcholy:
  • Riadok 16: Z fronty vyberieme jeden vrchol (v),
  • Riadok 17: V matici susednosti nájdeme všetkky vrcholy, ktoré susedia s vrcholom v.
  • Riadok 19: Ak vrhol i susedí v vrcholom v a zároveň vrchol v ešte nie je označkovaný:
  • Riadok 20: Vzdialenosť vrcholu i od vrcholu r bude vzdialenosť od r po v + 1
  • Riadok 21: Vrchol i označkujeme
  • Riadok 22: Vrchol i vložíme do fronty

Použité zdroje

• http://en.wikipedia.org/wiki/Breadth-first_search