Grafové algoritmy
Teória grafov je časť diskrétnej matematiky, ktorá skúma vlastnosti grafov.
Obsah
Graf
Graf G je usporiadaná dvojica (V,E), kde
- V – množina vrcholov
- E – množina hrán
Každá hrana e ([math]e\in E[/math]) je pár (v,w), kde [math]v,w\in V[/math]
Neorientovaný graf
Graf alebo neorientovaný graf G je usporiadaná dvojica G = (V, E), kde:
- V je neprázdna konečná množina vrcholov grafu,
- E je množina neusporiadaných dvojíc typu {u, v}, kde u ≠ v, nazývaných hrany grafu.
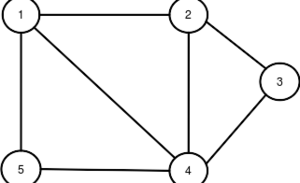
Príklad neorientovaného grafu:
- V={1,2,3,4,5}
E={(1,2),(1,4), (1,5), (2,4), (2,3), (3,4), (4,5)}
Orientovaný graf
Orientovaný graf alebo digraf G je usporiadaná dvojica G = (V, E), kde:
- V je neprázdna konečná množina vrcholov grafu,
- E je množina usporiadaných dvojíc typu (u, v), kde u ≠ v, nazývaných orientované hrany grafu.
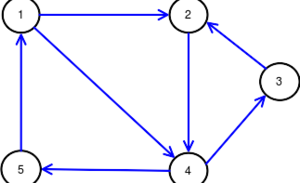
Príklad neorientovaného grafu:
- V={1,2,3,4,5}
E={(1,2),(1,4), (2,4), (3,2), (4,3), (4,5),(5,1)}
Hranovo ohodnotený graf
Hranovo ohodnotený graf je graf s ohodnotenými hranami.
Definícia: Graf G(v,e) sa nazýva hranovo ohodnotený, ak každej hrane [math]e\in E[/math] je priradené nejaké číslo [math]w\in R[/math].
Definícia: Kladne hranovo ohodnotený graf je taký graf G, w, že [math]w\left( e \right)\gt 0[/math]
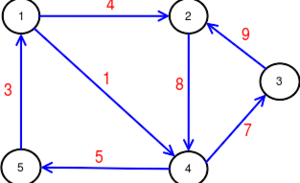
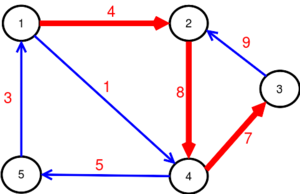
Príklad ohodnoteného orientovaného grafu:
- V={1,2,3,4,5}
E={(1,2,4),(1,4 ,1), (2,4,8), (3,2,9), (4,3,7), (4,5,5),(5,1,3)}
Základné pojmy v teórii grafov
- Cesta
- je postupnosť vrcholov spojených hranami grafu (Napríklad: c={1,2,4,3})
- Dĺžka cesty
- neohodnotený graf: je počet hrán v ceste (d=3),
- ohodnotený graf: súčet hodnôt na hraných grafu, ktoré sú v ceste (d=19)
- Stupeň vrcholu V
- počet hrán, vo vrchole V
- Cyklus
- V orientovanom grafe je cesta začínajúca a končiaca v tom istom vrchole a obsahujúca najmenej jednu hranu
- Strom
- je graf bez cyklov.
Reprezentácia grafov
Matica susednosti
Vzájomné súvislosti hrán a vrcholov sú popísané pomocou matice susednosti MG.
- Nech G=<V,E>;, [math]E\in \left\{ {{e}_{1}},{{e}_{2}},...,{{e}_{m}} \right\}[/math]
- Matica susednosti MG grafu G je štvorcová matica rádu m, kde
- [math]{{m}_{i,j}}=\langle \begin{matrix} 1,\ \ \text{Ak}\,\text{medzi}\,\text{vrcholmi i a j existuje hrana } \\ 0,\ \text{Ak}\,\text{medzi}\,\text{vrcholmi i a j nrexistuje hrana} \\ \end{matrix}[/math]
Príklad:
Matica susednosti pre neorienotvaný graf (na prvom obrázku)
- [math]{{M}_{G}}=\left( \begin{matrix} 0 & 1 & 0 & 1 & 1 \\ 1 & 0 & 1 & 1 & 0 \\ 0 & 1 & 0 & 1 & 0 \\ 1 & 1 & 1 & 0 & 1 \\ 1 & 0 & 0 & 1 & 0 \\ \end{matrix} \right)[/math]
Matica susednosti pre orienotvaný graf (na druhom obrázku)
- [math]{{M}_{G}}=\left( \begin{matrix} 0 & 1 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 1 \\ 1 & 0 & 0 & 0 & 0 \\ \end{matrix} \right)[/math]
Matica susednosti MG grafu G s ohodnotenými hranami:
Každému vrcholu je priradený zoznam jeho susedov (využitie lineárneho zoznamu).
- Matica susednosti MG grafu G je štvorcová matica rádu m, kde
- [math]{{m}_{i,j}}=\langle \begin{matrix} 1,\ \ \text{Ak}\,\text{medzi}\,\text{vrcholmi i a j existuje hrana } \\ c,\ \text{Ak}\,\text{medzi}\,\text{vrcholmi i a j nrexistuje hrana} \\ \end{matrix}[/math]
Matica susednosti pre orienotvaný ohodnotený graf (na treťom obrázku)
- [math]{{M}_{G}}=\left( \begin{matrix} 0 & 4 & 0 & 1 & 0 \\ 0 & 0 & 0 & 8 & 0 \\ 0 & 9 & 0 & 0 & 0 \\ 0 & 0 & 7 & 0 & 5 \\ 3 & 0 & 0 & 0 & 0 \\ \end{matrix} \right)[/math]
Implementácia matice susednosti v jazyku C
Úloha:Vytvorte maticu susednosti pre graf G. Graf G bude zadávaný nasledovne:
prvý bude počet vrcholov (pocetV) a potom počet hrán (pocetH) grafu G. Potom bude nasledovať pocetH dvojíc vrcholov + cena hrany c.
Vzorový vstup:
5 7 1 2 4 1 4 1 2 4 8 3 2 9 4 3 7 4 5 5 5 1 3
Analýza úlohy
Vlastnosť matice susednosti neorientovaného grafu je, že daná matica je súmerná vzhľadom na hlavnú diagonálu. Túto vlastnosť môžeme formulovať nasledovne: ak vrchol i susedí s vrcholom j, tak potom aj vrchol j susedí s vrcholom i.
Pri orientovaných grafoch takéto tvrdenie nemôžeme povedať, pretože ak existuje iba orientovaná hrana s vrcholu i do vrcholu j, tak potom neexistuje spôsob ako sa z vrcholu j dostať do vrcholu i.
Príprava dátovej štruktúry dvojrozmerné pole celých čísel (matica susednosti)
int i,j,pocetV,pocetH,v1,v2,c;
cin>>pocetV>>pocetH;
int **Mg=new int*[pocetV];
for(i=0;i<pocetV;i++)
Mg[i]=new int[pocetV];
// vynulovanie matice
//Mg predstavuje pr8zdny graf.
for(i=0;i<pocetV;i++)
for(j=0;j<pocetV;j++)
Mg[i][j]=0;
Vytvorenie orientovaného grafu
for(i=0;i<pocetH;i++)
{ cin>>v1>>v2>>c;
Mg[v1-1][v2-1]=c;
}
Vytvorenie neorientovaného grafu
for(i=0;i<pocetH;i++)
{ cin>>v1>>v2>>c;
Mg[v1-1][v2-1]=c;
Mg[v2-1][v1-1]=c;
}
Zoznam vrcholov
Grafové algoritmy
V súvislosti s grafmi existuje veľa úloh, ktoré sa dajú efektívne riešiť práve pomocou grafov. Napríklad:
- Prechádzanie stromom
- Hľadanie najkratšej cesty
- Prehľadávanie bludiska
- Hľadanie optimálnej cesty
- Ofarbenie grafu - problém ofarbenia politickej mapy sveta
- Toky v sieťach (elektrické schémy)
- Rozdhodovacie stromy
- a mnohé iné[1]
Medzi najzaujímavejšie úlohy patria úlohy o prehľadávaní grafu a hľadaní najkratšej (optimálnej) cesty. Hovoríme o nasledujúcich algoritmoch: