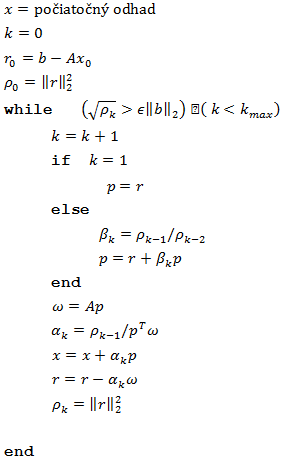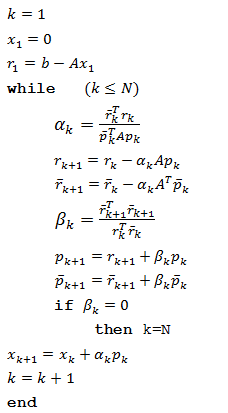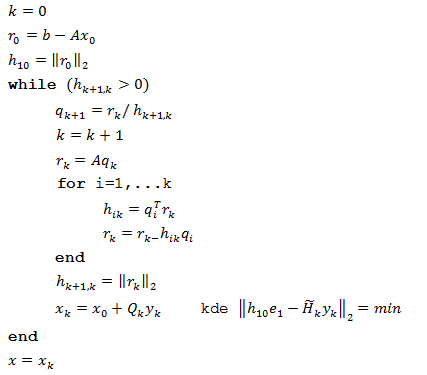Moderné metódy riešenia veľkých sústav rovníc
Obsah
V tejto časti sú opísané niektoré z moderných iteračných metód, ktoré sú vhodné pre riešenie veľmi veľkých a riedkych matíc. Sú tu opísané gradientné metódy a taktiež multigridové metódy. Tieto metódy využívajú mnohé zo simulačných softvérov, kde je potrebné riešiť veľké riedke sústavy lineárnych rovníc.
Metóda konjugovaných gradientov (CG)
Väčšina iteračných metód je závislá na parametroch, avšak niekedy je veľmi náročné zvoliť správne parametre. Toto nie je potrebné pri metóde konjugovaných gradientov (Conjugate Gradient Method). Táto metóda sa používa pre riešenie pre veľkých riedkych systémov, pretože sa v nej často využíva len násobenie matice sústavy vektorom. Metóda konjugovaných gradientov je vhodná pre symetrické a kladne definitné systémy[3]. </nowiki>
Majme systém rovníc Ax=b, kde A je štvorcová symetrická kladne definitná matica.
Využíva sa tu fakt, že riešenie takejto sústavy je jediným minimom nasledovnej formy:
|
[math]\phi \left( x \right)=\frac{1}{2}{{x}^{T}}Ax-{{x}^{T}}b[/math] |
(4.1) |
[3][9]
Minimum funkcie [math]\phi \left( x \right)[/math] je [math]-{{b}^{T}}{{A}^{-1}}b/2[/math], čo sme dostali dosadením za x , [math]x={{A}^{-1}}b[/math].
Potom teda minimalizácia funkcie [math]\phi \left( x \right)[/math] a riešenie rovnice [math]Ax=b[/math], sú ekvivalentné problémy ak je matica A symetrická kladne definitná.
Jedným z najjednoduchších spôsobov pre minimalizáciu je tzv. metóda najväčšieho spádu. V nejakom bode [math]x_c[/math] funkcia ϕ klesá najviac v smere záporného gradientu:[math]-\nabla \phi \left( {{x}_{c}} \right)=b-A{{x}_{c}}[/math].
Potom [math]{{r}_{c}}=b-A{{x}_{c}}[/math]. Hovoríme že, rc je reziduálny vektor v bode xc. Ak je reziduálny vektor nenulový , potom existuje kladné α , také že [math]\phi \left( {{x}_{c}}+\alpha {{r}_{c}} \right)\lt \phi \left( {{x}_{c}} \right)[/math]. Pre minimalizáciu dosadíme za α:
[math]\alpha =\frac{r_{c}^{T}{{r}_{c}}}{r_{c}^{T}A{{r}_{c}}}[/math]
[math]\phi \left( {{x}_{c}}+\alpha {{r}_{c}} \right)=\phi \left( {{x}_{c}} \right)-\alpha r_{c}^{T}{{r}_{c}}+\frac{1}{2}{{\alpha }^{2}}r_{c}^{T}A{{r}_{c}}[/math]
Budeme uvažovať o minimalizácii pozdĺž smerov {p1,p2,....} . V tejto metóde sa volia vektory pk tak, že vzniknú A-ortogonalizáciou vektora rezíduí . A-ortogonalizácia umožňuje z postupnosti lineárne nezávislých vektorov u1 , ... , un zostrojiť inú postupnosť lineárne nezávislých vektorov v1 , ... , vn tak , že bude platiť nasledovný vzťah [math]v_{i}^{T}A{{v}_{j}}=0\,pre\,i\ne j[/math]
Možno dokázať, že minimum funkcie [math]\phi \left( {{x}_{k-1}}+\alpha {{p}_{k}} \right)[/math] dostaneme pre
[math]\alpha ={{\alpha }_{k}}=p_{k}^{T}{{r}_{k-1}}/p_{k}^{T}A{{p}_{k}}[/math].
Dostávame [math]{{x}_{k}}={{x}_{k-1}}+{{\alpha }_{k}}{{p}_{k}}[/math], kde [math]p_k[/math] je spádový smer a [math]{{\alpha }_{k}}[/math] je optimálny krok[3].
Ak [math]{{r}_{k-1}}\ne 0[/math], potom existuje [math]p_k[/math] také, že [math]p_{k}^{T}{{r}_{k-1}}\ne 0[/math]. Keď je [math]k=1[/math] potom [math]{{p}_{1}}={{r}_{0}}[/math]. Pre k > 1 potom platí : [math]{{p}_{k}}={{r}_{k-1}}+{{\beta }_{k}}{{p}_{k-1}}[/math].
Keď [math]p_{k-1}^{T}A{{p}_{k}}=0[/math], potom dostávame vzťah : [math]{{\beta }_{k}}=-\frac{p_{k-1}^{T}A{{r}_{k-1}}}{p_{k-1}^{T}A{{p}_{k-1}}}[/math]
Reziduálny vektor [math]r_k[/math] môžeme vyjadriť ako [math]{{r}_{k}}={{r}_{k-1}}-{{\alpha }_{k}}A{{p}_{k}}[/math].
Potom použitím nasledovných substitúcií [math]\begin{align} & r_{k-1}^{T}{{r}_{k-1}}=-{{\alpha }_{k-1}}r_{k-1}^{T}A{{p}_{k-1}} \\ & r_{k-2}^{T}{{r}_{k-2}}={{\alpha }_{k-1}}p_{k-1}^{T}A{{p}_{k-1}} \\ \end{align}[/math]
vo vzťahu pre [math]{{\beta }_{k}}[/math] dostávame výsledný algoritmus.
Algoritmus CG
k=0
r_0=b-Ax_0
while r_k≠0
k=k+1
if k=1
p_1=r_0
else
β_k=r_(k-1)^T*r_(k-1)/r_(k-2)^T*r_(k-2)
p_k=r_(k-1)+β_k*p_(k-1)
end
α_k=r_(k-1)^T*r_(k-1)/p_k^T*Ap_k
x_k=x_(k-1)+α_k*p_k
r_k=r_(k-1)+α_k*Ap_k
end
x=x_k
V praxi sa však používa obmenená verzia tohto algoritmu, pretože zaokrúhľovacie chyby vedú k strate ortogonálnosti nad rezidúami a preto by nebolo zaručené ukončenie algoritmu. Preto je ukončenie algoritmu založené na maxime iterácií kmax a norme rezidua a danej presnosti ϵ. Toto vedie k nasledovnému algoritmu .
Upravený algoritmus CG:
Metóda konjugovaných gradientov konverguje k riešeniu sústavy rovníc o n neznámych najneskôr za n krokov. Tento algoritmus vyžaduje jedno násobenie matica-vektor a 10n flops za jednu iteráciu [3] .
Ilustračný príklad riešenia prostredníctvom metódy CG
Pre ilustráciu riešenia prostredníctvom metódy konjugovaných gradientov riešme jednoduchý príklad. Majme sústavu lineárnych rovníc Ax=b , kde A je symetrická matica o rozmeroch 2×2.
[math]\text{A}=\left[ \begin{matrix} 2 & 1 \\ 1 & 3 \\ \end{matrix} \right],\ x=\left[ \begin{matrix} {{x}_{1}} \\ {{x}_{2}} \\ \end{matrix} \right],\ b=\left[ \begin{matrix} 2 \\ 3 \\ \end{matrix} \right][/math]
Najprv zvolíme počiatočný odhad riešenia x0 .
[math]x=\left[ \begin{matrix} 1 \\ 1 \\ \end{matrix} \right][/math]
Riešenie Určíme reziduálny vektor [math]r_0[/math] ku [math]x_0[/math] prostredníctvom vzťahu [math]r_0=b-Ax_0[/math]. V našom prípade :
[math]{{r}_{0}}=\left[ \begin{matrix} 2 \\ 3 \\ \end{matrix} \right]-~\left[ \begin{matrix} 2 & 1 \\ 1 & 3 \\ \end{matrix} \right]\left[ \begin{matrix} 1 \\ 1 \\ \end{matrix} \right]=~\left[ \begin{matrix} 2 \\ 3 \\ \end{matrix} \right]-~\left[ \begin{matrix} 3 \\ 4 \\ \end{matrix} \right]=\left[ \begin{matrix} -1 \\ -1 \\ \end{matrix} \right][/math]
Toto je prvá iterácia , preto zvolíme za smer [math]p_0[/math] reziduálny vektor [math]r_0[/math]. Ďalej určíme skalár [math]α_0[/math] nasledovne
[math]{{\alpha }_{0}}=\frac{r_{0}^{T}{{r}_{0}}}{p_{0}^{T}A{{p}_{0}}}=\frac{\begin{matrix} \left[ \begin{matrix} -1 & -1 \\ \end{matrix} \right] & \left[ \begin{matrix} -1 \\ -1 \\ \end{matrix} \right] \\ \end{matrix}}{\begin{matrix} \left[ \begin{matrix} -1 & -1 \\ \end{matrix} \right] & \left[ \begin{matrix} 2 & 1 \\ 1 & 3 \\ \end{matrix} \right] & \left[ \begin{matrix} -1 \\ -1 \\ \end{matrix} \right] \\ \end{matrix}}=\frac{2}{7}[/math]
Vypočítame [math]x_1[/math] použitím nasledovného vzorca :
[math]{{x}_{1}}={{x}_{0}}+{{\alpha }_{0}}{{p}_{0}}=\left[ \begin{matrix} 1 \\ 1 \\ \end{matrix} \right]+\frac{2}{7}\left[ \begin{matrix} -1 \\ -1 \\ \end{matrix} \right]=\left[ \begin{matrix} 0.7143 \\ 0.7143 \\ \end{matrix} \right][/math]
Týmto sme ukončili prvú iteráciu a určili sme presnejšie približné riešenie systému . Teraz určíme ďalší reziduálny vektor [math]r_1[/math]:
[math]{{r}_{1}}={{r}_{0}}-{{\alpha }_{0}}A{{p}_{0}}=\left[ \begin{matrix} -1 \\ -1 \\ \end{matrix} \right]-\frac{2}{7}~\left[ \begin{matrix} 2 & 1 \\ 1 & 3 \\ \end{matrix} \right]~\left[ \begin{matrix} -1 \\ -1 \\ \end{matrix} \right]=\left[ \begin{matrix} -0.1429 \\ -0.1428 \\ \end{matrix} \right][/math]
Ďalším krokom výpočtu je určenie skalára [math]β_0[/math] ktorý sa použije na určenie ďalšieho smeru [math]p_1[/math]
[math]{{\beta }_{0}}=\frac{r_{1}^{T}{{r}_{1}}}{r_{0}^{T}{{r}_{0}}}=\frac{\left[ \begin{matrix} -0.1429 & -0.1428 \\ \end{matrix} \right]\left[ \begin{matrix} -0.1429 \\ -0.1428 \\ \end{matrix} \right]}{\begin{matrix} \left[ \begin{matrix} -1 & -1 \\ \end{matrix} \right] & \left[ \begin{matrix} -1 \\ -1 \\ \end{matrix} \right] \\ \end{matrix}}=0.0204[/math]
Teraz skalár [math]β_0[/math] použijeme pre určenie ďalšieho smeru [math]p_1[/math]
[math]{{p}_{1}}={{r}_{1}}+{{\beta }_{0}}{{p}_{0}}=\left[ \begin{matrix} -0.1429 \\ -0.1428 \\ \end{matrix} \right]+0,0204~\left[ \begin{matrix} -1 \\ -1 \\ \end{matrix} \right]=\left[ \begin{matrix} -0,1633 \\ 0,1224 \\ \end{matrix} \right][/math]
Určíme α_1 podobne ako predtým [math]α_0[/math] , ale teraz použijeme nový smer [math]p_1[/math]
[math]{{\alpha }_{1}}=\frac{r_{1}^{T}{{r}_{1}}}{p_{1}^{T}A{{p}_{1}}}=\frac{\begin{matrix} \left[ \begin{matrix} -0.1429 & -0.1428 \\ \end{matrix} \right] & \left[ \begin{matrix} -0.1429 \\ -0.1428 \\ \end{matrix} \right] \\ \end{matrix}}{\begin{matrix} \left[ \begin{matrix} -0,1633 & 0,1224 \\ \end{matrix} \right] & \left[ \begin{matrix} 2 & 1 \\ 1 & 3 \\ \end{matrix} \right] & \left[ \begin{matrix} -0,1633 \\ 0,1224 \\ \end{matrix} \right] \\ \end{matrix}}=0.6999[/math]
Nakoniec určíme [math]x_2[/math] podobným spôsobom ako predtým [math]x_1[/math] [10].
[math]{{x}_{2}}={{x}_{1}}+{{\alpha }_{1}}{{p}_{1}}=\left[ \begin{matrix} 0.7143 \\ 0.7143 \\ \end{matrix} \right]+0.6999\left[ \begin{matrix} -0,1633 \\ 0,1224 \\ \end{matrix} \right]=\left[ \begin{matrix} 0.600006 \\ 0.799967 \\ \end{matrix} \right][/math]
Dostávame riešenie sústavy [math]x=\left[ \begin{matrix} 0.600006 \\ 0.799967 \\ \end{matrix} \right][/math]
Overenie výsledku pomocou priamej metódy
Pre určenie presného riešenia sústavy použijeme Cramerovo pravidlo. Pre danú sústavu Ax=b , kde [math]\text{A}=\left[ \begin{matrix} 2 & 1 \\ 1 & 3 \\ \end{matrix} \right],\ x=\left[ \begin{matrix} {{x}_{1}} \\ {{x}_{2}} \\ \end{matrix} \right],\ b=\left[ \begin{matrix} 2 \\ 3 \\ \end{matrix} \right][/math]
Najprv zvolíme počiatočný odhad riešenia x0 .
[math]x=\left[ \begin{matrix} 1 \\ 1 \\ \end{matrix} \right][/math] určíme najskôr determinant sústavy [math]D=\left| \begin{matrix} 2 & 1 \\ 1 & 3 \\ \end{matrix} \right|=2*3-1*1=5[/math]
Potom nahradíme prvý stĺpec matice A vektorom pravých strán b a určíme determinant:
[math]{{D}_{1}}=\left| \begin{matrix} 2 & 1 \\ 3 & 3 \\ \end{matrix} \right|=2*3-1*3=3[/math]
Podobne nahradíme druhý stĺpec matice A a dostávame :
[math]{{D}_{2}}=\left| \begin{matrix} 2 & 2 \\ 1 & 3 \\ \end{matrix} \right|=2*3-2*1=4[/math]
Teraz určíme riešenie sústavy:
[math]\begin{align} & {{x}_{1}}=\frac{{{D}_{1}}}{D}=\frac{3}{5}=0.6 \\ & {{x}_{2}}=\frac{{{D}_{2}}}{D}=\frac{4}{5}=0.8 \\ \end{align}[/math]
Metóda bikonjugovaných gradientov (BCG)
Metóda konjugovaných gradientov je vhodná len pre symetrické kladne definitné systémy. V prípade nesymetrických a nie nutne kladne definitných matíc sa používa metóda bikonjugovaných gradientov. Metóda bikonjugovaných gradientov sa vzťahuje k všeobecnej sústave a preto nemá bezprostrednú minimalizačnú interpretáciu. Táto metóda je založená na úprave sústavy Ax=b na [math]{{A}^{T}}Ax={{A}^{T}}b[/math]. Teória k tejto metóde je opísaná v [3] a [11]. Metóda bikonjugovaných gradientov je definovaná nasledovným algoritmom:
Algoritmus BCG:
V prípade, že matica A je symetrická, tak [math]{{\overline{p}}_{k}}={{p}_{k}}[/math] a [math]{{\overline{r}}_{k}}={{r}_{k}}[/math], čiže vlastne metóda konjugovaných gradientov je špeciálnym prípadom metódy bikonjugovaných gradientov [3] [11].
Generalized Minimal Residual Method (GMRES)
Metóda GMRES vychádza z Arnoldiho metódy, ktorá je podrobne opísaná v [3]. GMRES sa používa pre nesymetrické matice. Arnoldiho metóda vychádza z tzv. Hessenbergovho rozkladu [math]{{Q}^{T}}AQ=H[/math]. Ak [math]Q=[{{q}_{1}},\ldots {{q}_{n}}][/math] a porovnáme stĺpce v [math]AQ=QH[/math] potom
[math]A{{q}_{k}}=\underset{i=1}{\overset{k+1}{\mathop \sum }}\,{{h}_{ik}}{{q}_{i}}~~,~kde~1\le k\le n-1[/math]
Keď vyberieme posledný výraz v sumácii, dostaneme
[math]{{h}_{k+1,k}}{{q}_{k+1}}=A{{q}_{k}}\underset{i=1}{\overset{k}{\mathop \sum }}\,{{h}_{ik}}{{q}_{i}}~~:\equiv {{r}_{k}}~~,~\text{kde}~~~~~{{h}_{ik}}=q_{i}^{T}A{{q}_{k}}~~~\text{ }\!\!~\!\!\text{ pre}~i=1~,~\ldots ~k[/math]
Ak [math]r_k≠0[/math] , potom [math]q_{k+1}[/math] je určené ako [math]{{q}_{k+1}}={{r}_{k}}/{{h}_{k+1,k}}[/math] pričom [math]{{h}_{k+1,k}}=\left\| {{\left. {{r}_{k}} \right\|}_{2}} \right.[/math]. Vektory [math]q_k[/math] sú Arnoldiho vektory. Hlavnou myšlienkou metódy GMRES je vyjadriť iterácie x_k prostredníctvom Arnoldiho vektorov . Prostredníctvom Arnoldiho iterácií dostaneme rozklad:
[math]A{{Q}_{k}}={{Q}_{k+1}}{{\tilde{H}}_{k}}[/math]
kde stĺpce matice [math]{{Q}_{k+1}}=[{{Q}_{k}}{{q}_{k+1}}][/math] sú ortonormálne Alrnoldiho vektory a matica [math]{{\tilde{H}}_{k}}[/math] je horná Hessenbergova matica.
[math]{{\tilde{H}}_{k}}=\left[ \begin{matrix} {{h}_{11}} & {{h}_{12}} & \cdots & \cdots & {{h}_{1k}} \\ {{h}_{21}} & {{h}_{22}} & \cdots & \cdots & {{h}_{2k}} \\ 0 & \ddots & \ddots & {} & \vdots \\ \vdots & {} & \ddots & \ddots & \vdots \\ 0 & \cdots & \cdots & {{h}_{k,k-1}} & {{h}_{kk}} \\ 0 & \cdots & \cdots & 0 & {{h}_{k+1,k}} \\ \end{matrix} \right][/math]
V k-tom kroku GMRES sa výraz [math]{{\left\| b-A{{x}_{k}} \right\|}_{2}}[/math] minimalizuje, kde [math]{{x}_{k}}={{x}_{0}}+{{Q}_{k}}{{y}_{k}}[/math]. Ak [math]{{q}_{1}}=\frac{{{r}_{0}}}{{{\rho }_{0}}}[/math], kde [math]{{\rho }_{0}}={{\left\| {{r}_{0}} \right\|}_{2}}[/math], potom
[math]{{\left\| b-A\left( {{x}_{0}}+{{Q}_{k}}{{y}_{k}} \right) \right\|}_{2}}={{\left\| {{r}_{0}}-A{{Q}_{k}}{{y}_{k}} \right\|}_{2~}}={{\left\| {{r}_{0}}-A{{Q}_{k+1}}{{{\tilde{H}}}_{k}}{{y}_{k}} \right\|}_{2}}=~{{\left\| {{p}_{0}}{{e}_{1}}-{{{\tilde{H}}}_{k}}{{y}_{k}} \right\|}_{2}}[/math]
Iterácia pri metóde GMRES je daná vzťahom [math]{{x}_{k}}={{x}_{0}}+{{Q}_{k}}{{y}_{k}}[/math].
Algoritmus GMRES
Ak A je nesingulárna matica, a x0 je počiatočný odhad riešenia [math]\left( A{{x}_{0}}\approx b \right)[/math] potom nasledovný algoritmus vypočíta x, tak že platí [math]Ax=b[/math].
Multigridové metódy (MG)
Multigridové metódy sú jedny z najrýchlejších numerických algoritmov pre riešenie veľkých riedkych systémov . Všetky multigridové metódy sú majú základný princíp rovnaký . Daný problém je riešený použitím rôznych úrovní riešenia pre určenie výsledného riešenia. Multigridové metódy zlepšujú konvergenciu takým spôsobom, že sa určí približné riešenie systému použitím riedkej siete (grid). Táto približná hodnota sa následne použije ako počiatočná hodnota iterácií pri použití hustejšej siete . Potom sa výsledok podobne použije v ďalšej iterácii a takto sa postupne dostaneme až k výslednému riešeniu. Multigridové metódy teda zahŕňajú hierarchiu sietí, ktoré opisujú danú úlohu, pre rôzne veľkosti elementov mriežky. Na tomto je založený geometrický multigrid. Naopak algebraický multigrid využíva multigridové riešenie daného systému bez použitia geometrickej informácie z hierarchie sietí, ale využíva len pôvodný lineárny systém [13].
Princíp multigridových metód
Majme sústavu lineárnych rovníc, ktorá vznikla diskretizáciou nejakej spojitej úlohy.
|
[math]{{A}_{h}}{{u}_{h}}={{f}_{h}}[/math] |
(4.1) |
kde A_hje matica systému, u je vektor riešení hľadanej veličiny, f reprezentuje danú pravú stranu. Presné riešenie rovnice (4.1) je označené ako [math]u_{h}^{*}[/math] a potom [math]u_h[/math] je aproximáciou k [math]u_{h}^{*}[/math].
Ďalej zavedieme index iterácie , napr. [math]u_{h}^{(k)}[/math] predstavuje k-tu iteráciu. Budeme uvažovať, že šírka ľubovoľnej riedkej siete H sa získa ako [math]H=2h[/math] , kde h je šírka nasledujúcej hustejšej mriežky. Indexy h a H slúžia pre rozlíšenie či sa jedná o mriežku so šírkou h alebo H.
Reziduálny vektor prislúchajúci aproximácii u_h je definovaný ako
|
[math]{{r}_{h}}:={{f}_{h}}-{{A}_{h}}{{u}_{h}}[/math] |
(4.2) |
Algebraická chyba zodpovedajúca k aktuálnej aproximácii [math]u_h[/math] je daná ako
|
[math]{{e}_{h}}:=~u_{h}^{*}-{{u}_{h}}[/math] |
(4.3) |
Z toho potom dostávame [math]{{A}_{h}}{{e}_{h}}={{A}_{h}}\left( u_{h}^{*}-{{u}_{h}} \right)={{A}_{h}}u_{h}^{*}-{{A}_{h}}{{u}_{h}}={{f}_{h}}-{{A}_{h}}{{u}_{h}}={{r}_{h}}[/math], teda dostávame tzv. reziduálnu rovnicu, ktorá vyjadruje vzťah medzi chybou [math]e_h[/math] a reziduálnym vektorom [math]r_h[/math]:
|
[math]{{A}_{h}}{{e}_{h}}={{r}_{h}}[/math] |
(4.4) |
Vyjadrenie reziduálnej rovnice prostredníctvom riedkej siete
Aplikovaním niekoľkých iterácií vhodnej klasickej iteračnej metódy na nasledujúcu hustejšiu sieť sa vyhladí algebraická chyba . Táto technika sa nazýva pre-smoothing . Potom aproximácia k tzv. hladkej chybe môže byť efektívne vypočítaná na redšej sieti, použitím reziduálnej rovnice (4.4) . Následne musí byť táto hladká chyba interpolovaná späť pre hustú mriežku a podľa vzťahu (4.3) pripočítaná ku aktuálnej aproximácii pre hustú sieť. Reziduálna rovnica (4.4) pre riedku sieť je potom vyjadrená nasledovne:
|
[math]{{A}_{H}}{{e}_{H}}={{r}_{H}}[/math] |
(4.5) |
kde [math]A_H[/math] je matica v riedkej siete a [math]e_H[/math],[math]r_H[/math] sú chyba [math]e_h[/math], resp. reziduálny vektor [math]r_h[/math] vyjadrené pre riedku sieť [13]. Operátory pre transformáciu medzi sieťami
Pre prevod medzi sieťami je potrebné určiť nasledovné operátory :
- Operátor interpolácie [math]I_{H}^{h}:~~~{{\mathbb{R}}^{{{n}_{H}}}}\to {{\mathbb{R}}^{{{n}_{h}}}}[/math]
- slúži na transformáciu z riedkej siete do hustej
- Operátor reštrikcie [math]I_{h}^{H}:~~~{{\mathbb{R}}^{{{n}_{h}}}}\to {{\mathbb{R}}^{{{n}_{H}}}}[/math]
- slúži na transformáciu z hustej siete do riedke [12][13].
Algoritmus dvojgridovej metódy
- Vykoná sa ν_1 iterácií pre vyhladenie vysokofrekvenčných chýb na [math]\Omega^h[/math] predvyhladenie (pre-smoothing) [math]u_{h}^{\left( k+\frac{1}{3} \right)}\leftarrow S_{h}^{{{\nu }_{1}}}\left( u_{h}^{\left( k \right)} \right)[/math]
- Vypočíta sa reziduálny vektor na [math]\Omega^h[/math]: [math]{{r}_{h}}\leftarrow {{f}_{h}}-{{A}_{h}}u_{h}^{\left( k+\frac{1}{3} \right)}[/math]
- Prevedie sa reziduálny vektor z [math]\Omega^h[/math] do [math]\Omega^H[/math] a inicializuje sa aproximácia [math]u_H[/math]: [math]{{f}_{H~~}}\leftarrow I_{h}^{H}{{r}_{h}}~~~,~{{u}_{H}}\leftarrow 0[/math]
- ak [math]\Omega^H[/math]
- je najredšia sieť z hierarchie, potom sa rieši [math]{{A}_{H}}{{u}_{H}}={{f}_{H}}[/math] presne
- inak, rieši sa [math]{{A}_{H}}{{u}_{H}}={{f}_{H}}[/math] približne rekurzívnym vykonávaním multigridového [math]V\left( {{\nu }_{1}},{{\nu }_{2}} \right)[/math] -cyklu začínajúc od [math]\Omega^H[/math]
- Interpoluje sa aproximácia (t.j. chyba) z [math]\Omega^H[/math] do [math]\Omega^h[/math]: [math]{{{\tilde{e}}}_{h}}\leftarrow I_{H}^{h}{{u}_{H}}[/math]
- Vykoná sa korekcia aproximácie na [math]\Omega^h[/math]: [math]u_{h}^{\left( k+\frac{2}{3} \right)}\leftarrow u_{h}^{\left( k+\frac{1}{3} \right)}+{{{\tilde{e}}}_{h}}[/math]
- Vykoná sa [math]ν_2[/math] iterácií pre vyhladenie vysokofrekvenčných chýb na [math]\Omega^h[/math]. Dodatočné vyhladenie (post-smoothing): [math]u_{h}^{\left( k+1 \right)}\leftarrow S_{h}^{{{\nu }_{2}}}\left( u_{h}^{\left( k+\frac{2}{3} \right)} \right)[/math]
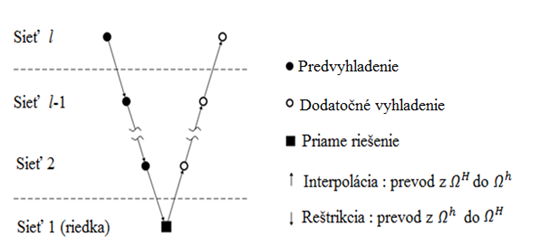
Dostávame V-cyklus pre dvojgridovú metódu[12] [13]. Tento algoritmus predpokladá, že v každej iterácii bude rovnica riedkej siete riešená presne. Avšak , ak je tento lineárny systém príliš veľký na to , aby mohol byť efektívne riešený priamou metódou prípadne klasickou iteračnou metódou , možno tento algoritmus aplikovať rekurzívne . Dostávame sa k rekurzívnej definícii multigridového cyklu (obr. 1 ) [12].
Geometrický multigrid (GMG)
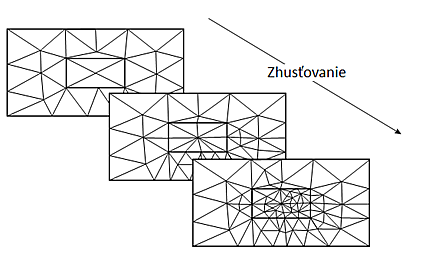
Na rozdiel od štandardných techník riešenia metódy konečných prvkov, geometrický multigrid nie je založený na pevnej konečno prvkovej sieti (grid), ktorá opisuje neznáme pole premenných dostatočne presne. Geometrický MG začína od veľmi riedkej priestorovej diskretizácie T1 danej oblasti. Rozčlenením elementov T1 dospejeme k hustejšej diskretizácii T2. Tento proces zhusťovania (obr. 2) môže zahŕňať všetky elementy alebo iba časť elementov. Opakovaným zhusťovaním siete získame hierarchiu rozčlenení [math]{{T}_{1}}~,~...~,~{{T}_{l}}[/math] pre ktoré sú systémy [math]{{A}_{q}}{{u}_{q}}={{f}_{q}}[/math] kde [math]q=1,2,\ldots ,l[/math] zostavené a môže sa vykonať multigridový cyklus (obr.1) [12].
Ilustračný príklad
Pre ilustráciu riešenia prostredníctvom metódy geometrického multigridu, resp. dvojgridovej metódy, riešme jednoduchý príklad. Majme jednoduchú diferenciálnu rovnicu bez pravej strany [math]-2{{y}^{''}}=0[/math] na intervale <0,4> s okrajovými podmienkami [math]y(0)=0 ,y(4)=1[/math]
Diskretizáciou tejto parciálnej diferenciálnej rovnice dostaneme maticovú rovnicu [16] . Majme teda rovnicu [math]{{A}_{h}}\text{ }\!\!~\!\!\text{ }{{u}_{h}}=\text{ }\!\!~\!\!\text{ }\!\!~\!\!\text{ }{{f}_{h}}[/math].
[math]{{A}_{h}}=\left[ \begin{matrix} 1 & 0 & 0 & 0 & 0 \\ -2 & 4 & -2 & 0 & 0 \\ 0 & -2 & 4 & -2 & 0 \\ 0 & 0 & -2 & 4 & -2 \\ 0 & 0 & 0 & 0 & 1 \\ \end{matrix} \right],\ {{u}_{h}}=\left[ \begin{matrix} {{u}_{1}} \\ {{u}_{2}} \\ {{u}_{3}} \\ {{u}_{4}} \\ {{u}_{5}} \\ \end{matrix} \right],\ {{f}_{h=}}\left[ \begin{matrix} 0 \\ 0 \\ 0 \\ 0 \\ 1 \\ \end{matrix} \right][/math]
Riešenie
1. krok
Prostredníctvom niekoľkých iterácií klasickej iteračnej metódy určíme počiatočnú hodnotu vektora [math]u_h[/math].
[math]u_{h}^{(k+\frac{1}{3})}=\left[ \begin{matrix} 0 \\ 0 \\ 0 \\ 0.5 \\ 1 \\ \end{matrix} \right][/math]
2. krok
Určíme reziduálny vektor [math]r_0[/math] na oblasti [math]\Omega_h[/math] podľa vzťahu [math]{{r}_{h}}={{f}_{h}}-{{A}_{h}}u_{h}^{\left( 1+\frac{1}{3} \right)}[/math]
[math]{{r}_{h}}=\left[ \begin{matrix} 0 \\ 0 \\ 0 \\ 0 \\ 1 \\ \end{matrix} \right]-\left[ \begin{matrix} 1 & 0 & 0 & 0 & 0 \\ -2 & 4 & -2 & 0 & 0 \\ 0 & -2 & 4 & -2 & 0 \\ 0 & 0 & -2 & 4 & -2 \\ 0 & 0 & 0 & 0 & 1 \\ \end{matrix} \right]\left[ \begin{matrix} 0 \\ 0 \\ 0 \\ 0.5 \\ 1 \\ \end{matrix} \right]=\left[ \begin{matrix} 0 \\ 0 \\ 1 \\ 0 \\ 0 \\ \end{matrix} \right][/math]
3. krok
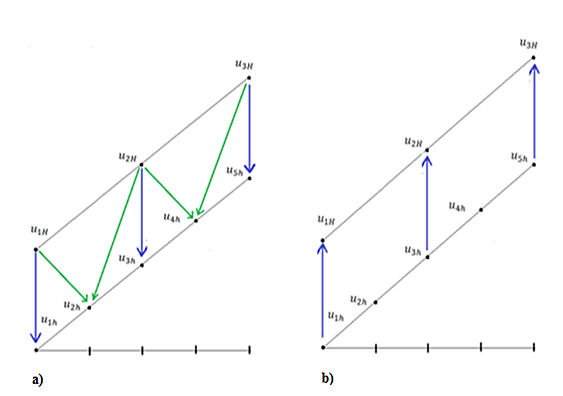
Pre transformáciu medzi sieťami je potrebné určiť operátory interpolácie a reštrikcie. Na obr. 3 je zobrazená interpolácia a reštrikcia.
Ako vidno na obr. 3a pri interpolácii sa hodnoty v bodoch riedkej siete transformovaním do hustej siete nezmenia. Hodnoty v bodoch, ktoré sa nachádzajú iba v hustej sieti sa určia ako priemer ich susedných bodov riedkej siete. Pri reštrikcii (obr. 3b) hodnoty v bodoch, ktoré sa nachádzajú v obidvoch sieťach , ostanú nezmenené [17]. Potom definujeme pre danú úlohu tieto operátory nasledovne:
Operátor interpolácie: [math]I_{H}^{h}=\left[ \begin{matrix} 1 & 0 & 0 \\ 0.5 & 0.5 & 0 \\ 0 & 1 & 0 \\ 0 & 0.5 & 0.5 \\ 0 & 0 & 1 \\ \end{matrix} \right][/math]
Operátor reštrikcie: [math]I_{h}^{H}=\left[ \begin{matrix} 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ \end{matrix} \right][/math]
Prostredníctvom operátora reštrikcie prevedieme reziduálny vektor z [math]\Omega^h[/math] do [math]\Omega^H[/math].
[math]{{f}_{H}}=I_{h}^{H}{{r}_{h}}=\left[ \begin{matrix}
1 & 0 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 & 0 \\
0 & 0 & 0 & 0 & 1 \\
\end{matrix} \right]\left[ \begin{matrix}
0 \\
0 \\
1 \\
0 \\
0 \\
\end{matrix} \right]=\left[ \begin{matrix}
0 \\
1 \\
0 \\
\end{matrix} \right][/math]
4. krok
Určíme [math]A_H[/math] prostredníctvom Galerkinovho vzťahu : [math]{{A}_{H}}=I_{h}^{H}{{A}_{h}}I_{H}^{h}[/math]
[math]\begin{align}
& {{f}_{H}}=I_{h}^{H}{{r}_{h}}=\left[ \begin{matrix}
1 & 0 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 & 0 \\
0 & 0 & 0 & 0 & 1 \\
\end{matrix} \right]\left[ \begin{matrix}
1 & 0 & 0 & 0 & 0 \\
-2 & 4 & -2 & 0 & 0 \\
0 & -2 & 4 & -2 & 0 \\
0 & 0 & -2 & 4 & -2 \\
0 & 0 & 0 & 0 & 1 \\
\end{matrix} \right]\left[ \begin{matrix}
1 & 0 & 0 \\
0.5 & 0.5 & 0 \\
0 & 1 & 0 \\
0 & 0.5 & 0.5 \\
0 & 0 & 1 \\
\end{matrix} \right]=\left[ \begin{matrix}
1 & 0 & 0 \\
-1 & 2 & -1 \\
0 & 0 & 1 \\
\end{matrix} \right] \\
& \\
\end{align}[/math]
Keďže máme len dve siete, tak toto je tá najredšia, teda s nej určíme riešenie priamou metódou.
[math]{{A}_{H}}{{u}_{H}}={{f}_{H}}[/math]
Riešenie tohto systému: [math]{{u}_{H}}=\left[ \begin{matrix} 0 \\ 0.5 \\ 0 \\ \end{matrix} \right][/math]
5. krok Interpolujeme [math]u_H[/math] z [math]\Omega^H[/math] do [math]\Omega^h[/math] a dostávame chybu [math]{{{\tilde{e}}}_{h}}[/math]
[math]{{{\tilde{e}}}_{h}}=I_{H}^{h}{{u}_{H}}=\left[ \begin{matrix}
1 & 0 & 0 \\
0.5 & 0.5 & 0 \\
0 & 1 & 0 \\
0 & 0.5 & 0.5 \\
0 & 0 & 1 \\
\end{matrix} \right]\left[ \begin{matrix}
0 \\
0.5 \\
0 \\
\end{matrix} \right]=\left[ \begin{matrix}
0 \\
0.25 \\
0.5 \\
0.25 \\
0 \\
\end{matrix} \right][/math]
6. krok
Vykonáme korekciu
[math]u_{h}^{\left( k+\frac{2}{3} \right)}=u_{h}^{\left( k+\frac{1}{3} \right)}+{{{\tilde{e}}}_{h}}=\left[ \begin{matrix} 0 \\ 0 \\ 0 \\ 0.5 \\ 1 \\ \end{matrix} \right]+\left[ \begin{matrix} 0 \\ 0.25 \\ 0.5 \\ 0.25 \\ 0 \\ \end{matrix} \right]=\left[ \begin{matrix} 0 \\ 0.25 \\ 0.5 \\ 0.75 \\ 1 \\ \end{matrix} \right][/math]
7. krok
Prostredníctvom klasickej iteračnej metódy môžeme vyhladiť prípadné vysokofrekvenčné chyby.
Výsledné riešenie sústavy je [math]{{u}_{h}}=\left[ \begin{matrix} 0 \\ 0.25 \\ 0.5 \\ 0.75 \\ 1 \\ \end{matrix} \right][/math]
Algebraický multigrid (AMG)
Na rozdiel od geometrického multigridu, algebraický multigrid nepotrebuje konečno prvkový opis danej úlohy s hierarchiou sietí . Geometrický MG vyžaduje regulárnu štruktúru riešeného problému, naopak algebraický MG je vhodnejší pre úlohy s neregulárnou štruktúrou. Matice [math]A_q[/math] s q=1,2,…,l na rôznych úrovniach sú nastavované iba z poznania matice [math]A_h= A_l[/math] z konečno prvkového rozkladu.
Keďže geometrický MG vyžaduje pre riešenie hierarchickú konečno prvkovú sieť, algebraický MG poskytuje vhodnú alternatívu hlavne v týchto prípadoch:
- Diskretizácia úlohy neposkytuje hierarchiu sietí, ktorá je nevyhnutná pre geometrický MG.
- Najredšia sieť pri použití geometrického MG je príliš veľká pre riešenie priamymi metódami alebo klasickými iteračnými metódami.
- Klasické iteračné metódy použité pri geometrickom MG nie sú dostatočne efektívne [12].
Podrobný opis ako aj algoritmus tejto metódy možno nájsť v [12].