Softvérové balíky pre riešenie veľkých lineárnych systémov

Z Kiwiki
Skočit na navigaci Skočit na vyhledávání

Obsah práce
1. Sústavy lineárnych rovníc a matice
2. Klasické metódy riešenia sústav lineárnych rovníc
3. Priame metódy pre riešenie veľkých sústav rovníc
4. Moderné metódy riešenia veľkých sústav rovníc
5. Softvérové balíky pre riešenie veľkých lineárnych systémov

Riešenie sústav lineárnych rovníc je základom riešenia mnohých problémov vo vedeckých výpočtoch. V mnohých prípadoch sú riešené sústavy veľmi veľké a matica sústavy je riedka. V mnohých aplikáciách je matica symetrická, ako je to napríklad pri použití metódy konečných prvkov. Za posledné desaťročia bolo navrhnutých množstvo nových algoritmov a taktiež programových balíkov pre riešenie symetrických riedkych matíc , ktoré implementujú tieto algoritmy. V tejto časti sú uvedené niektoré balíky obsahujúce priame riešiče riedkych lineárnych systémov.

Priame riešiče riedkych systémov pracujú v niekoľkých fázach. Presné rozdelenie do jednotlivých fáz závisí od použitého algoritmu a softvéru, všeobecné rozdelenie je nasledovné:

  1. Usporiadanie na základe štruktúry.
  2. Analýza štruktúry matice na základe, ktorej sa zavedú potrebné  dátové štruktúry pre efektívny rozklad matice
  3. Rozklad matice
  4. Fáza riešenia, kde sa vykoná eliminácia a potom následne spätná substitúcia.

Fáza rozkladu matice je obvykle časovo najnáročnejšia. Naopak fáza riešenia je všeobecne omnoho rýchlejšia.

Algoritmy rozkladu matíc

Rozklad môže vykonaný rôznymi spôsobmi, čo závisí od prístupu k jednotlivým prvkom systému. Existujú tri základné typy algoritmov : left-looking, right-looking a multifrontal.

Pri right-looking prístupe sa v každom kroku vypočítajú riadky a stĺpce a a tieto zmeny sa hneď aplikujú. Pri left-looking algoritme sa vypočítané zmeny neaplikujú hneď. Predtým ako je eliminovaný stĺpec k , všetky zmeny z predchádzajúcich stĺpcov k matice L sa použijú spolu so stĺpcom k matice A. Pri multifrontálnom algoritme sa zmeny akumulujú, a potom sa aplikujú prostredníctvom tzv. eliminačného stromu.


Niektoré knižnice pre priame riešenie riedkych systémov

PARDISO umožňuje paralelné a sériové riešenie nesymetrických a symetrických riedkych systémov na multiprocesorovom systéme so zdieľanou pamäťou .Využíva sa tu left-looking a right-looking verzia Choleského rozkladu.

SPOOLES je knižnica pre riešenie riedkych reálnych a komplexných sústav rovníc . Je dostupná v paralelnej aj sériovej verzii. Používa sa tu verzia Gaussovej eliminačnej metódy s Croutovou redukciou .

TAUCS je navrhnutá pre symetrické kladne definitné systémy . Používa sa tu left-looking a multifrontálne verzie LU rozkladu a Choleského rozkladu.

UMFPACK je knižnica pre riešenie nesymetrických systémov. Využíva nesymetrický multifrontálny LU rozklad [14].


Simulačný softvér

Existuje viacero softvérov, ktoré používajú metódu konečných prvkov. Pomocou tejto metódy sa transformuje systém parciálnych diferenciálnych rovníc, ktoré popisujú danú úlohu na systém lineárnych rovníc . Táto metóda sa používa v mnohých odvetviach : napr. pri návrhu strojov, rôznych súčiastok, atď.

Pri metóde konečných prvkov sa väčšinou dostávame k veľkému systému lineárnych rovníc . Pre jeho riešenie simulačné softvéry používajú niektoré z uvedených moderných metód . Je známych viacero softvérov ktoré pracujú s metódou konečných prvkov napr. ANSYS, COMSOL, FEMM, ELMER Multiphysics a mnoho ďalších. Pre riešenie vzniknutých veľkých sústav lineárnych rovníc používajú rôzne moderné metódy riešenia. V tab. 1 sú uvedené metódy používané v niektorých simulačných programoch.

Tab. č. 1 Metódy používané v simulačných softvéroch
FEMM ANSYS COMSOL ELMER MULTIPHYSICS
CG iteračné gradientné metódy knižnica UMFPACK knižnica UMFPACK
BCG AMG GMRES AMG a GMG
iteračné gradientné metódy

Ukážkový príklad analýzy vo FEMM

FEMM je softvérový balík pre riešenie nízkofrekvenčných elektromagnetických úloh v 2D. Pre riešenie vzniknutého systému lineárnych rovníc podľa typu riešeného problému používa buď metódu konjugovaných gradientov s prepodmienením alebo metódu bikonjugovaných gradientov [15].


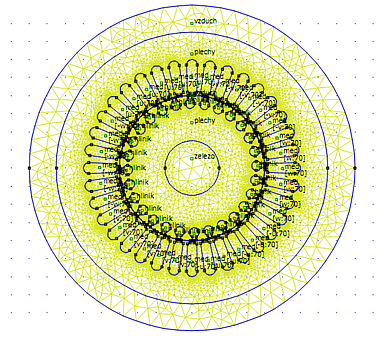
Na (obr.4) je 2D model asynchrónneho motora, pre ktorý hľadáme rozloženie potenciálu.


Obr. 4 Model asynchrónneho motora vo FEMM

Daná úloha má 38638 stupňov voľnosti, teda sa rieši maticová rovnica s maticou systému o rozmeroch 38638×38638.

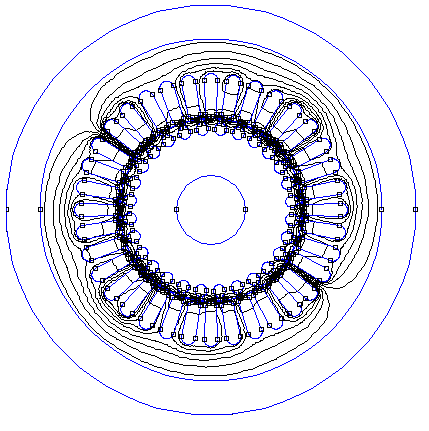
Obr. 5 Rozloženie poľa asynchrónneho motora

Na (obr. 5) je vyriešené rozloženie potenciálu pre daný asynchrónny motor. Riešenie danej úlohy metódou bikonjugovaných gradientov prostredníctvom softvéru FEMM trvalo 3 minúty. Riešenie bolo realizované na počítači s procesorom AMD Turion X2 Dual-Core 2.20 GHz a s operačnou pamäťou 4 GB.

Záver

Cieľom mojej práce bolo oboznámiť sa s riešením sústav veľkých lineárnych rovníc a opísať a porovnať niektoré z existujúcich algoritmov. V práci som sa zameral na opis niektorých existujúcich algoritmov pre riešenie sústav lineárnych rovníc.

V práci sú opísané niektoré klasické algoritmy pre riešenie sústav lineárnych rovníc. Cramerovo pravidlo a riešenie pomocou inverznej matice sú vhodné len pre veľmi malé sústavy. Gaussova eliminačná metóda taktiež pre veľké matice nie je príliš vhodná, pretože je potrebné veľké množstvo operácií pre riešenie veľkých sústav. Takisto pri eliminácii môžu vzniknúť chyby. Preto sa skôr používajú jej modifikácie. Klasické iteračné metódy: Jacobiho a Gauss – Seidelova sú vhodné pre väčšie matice a riedke matice. Keďže množstvo nulových prvkov v riedkych maticiach znižuje počet potrebných operácií a výpočtovú náročnosť, sú tieto metódy vhodné aj pre veľké riedke sústavy lineárnych rovníc.

Ďalšia časť sa zaoberá priamymi metódami pre riešenie veľkých sústav. Sú tu opísané dva algoritmy rozkladu pre zjednodušenie veľkých matíc: LU rozklad a Choleského rozklad. Je viacero metód, ako možno rozložiť maticu do podoby niektorého z rozkladov. Na týchto rozkladoch sú založené niektoré moderné priame metódy. V tejto práci sú opísané len základné algoritmy, ako možno tieto rozklady uskutočniť.

Hlavná časť práce je venovaná moderným iteračným metódam riešenia veľkých sústav. Pozornosť sa tu venuje tzv. gradientným metódam a multigridovým metódam. Pri gradientných metódach sa zostrojí postupnosť vektorov , ktorá konverguje k riešeniu sústavy. Metóda konjugovaných gradientov je vhodná len pre symetrické kladne definitné matice, naopak metóda bikonjugovaných gradientov a GMRES sa používajú pre nesymetrické systémy. Je tu vypracovaný aj ukážkový príklad riešenia sústavy malých rozmerov prostredníctvom metódy konjugovaných gradientov. Ďalej sa táto časť zaoberá multigridovými metódami. Geometrické multigridové metódy vyžadujú informáciu o hierarchii daného systému, naopak algebraické multigridové metódy nepotrebujú túto hierarchiu poznať. Algebraické sú vhodnejšie pre úlohy s neregulárnou štruktúrou. Pre objasnenie metódy geometrického multigridu sme vypracovali ukážkový príklad riešenia jednoduchej úlohy.

Posledná časť práce sa zaoberá aplikáciou a použitím daných metód. Sú tu opísané niektoré knižnice ktoré v sebe implementujú niektoré z uvedených metód. Taktiež sú tu opísané simulačné programy, ktoré využívajú niektoré z týchto metód a knižníc.

Použitá literatúra

  1. Parallel Algorithms for Matrix Computations. Philadelphia : Society for Industrial and Applied Mathematics, 1990. 195 s. ISBN 0898712602
  2. TIMOTHY A. Davis: Direct Methods for Sparse Linear Systems : Fundamentals of Algorithms. Society for Industrial and Applied Mathematic, 2006. 217 s. ISBN 0898716136.
  3. GOLUB G. H. , Van Loan Ch. F., Matrix computations, The John Hopkins University Press, 1996. 694 s. ISBN 0801854148
  4. FAJMON, Bretislav , RUŽICKOVÁ, Irena. Matematika 3. Brno : Vysoké Učení Technické v Brne, 2005. 252 s. Dostupný z WWW: <http://www.umat.feec.vutbr.cz/~fajmon/inm/matematika3.pdf>.
  5. Skriptá, Bratislava: STU, Dostupný z WWW:<http://www-kmadg.svf.stuba.sk/skripta/index.html>.
  6. DOBÁK, Radoslav. Využitie blokových matíc pri riešení úloh lineárnej algebry . Bratislava, 2009. 51 s. Univerzita Komenského v Bratislave. Dostupné z WWW: <http://www.iam.fmph.uniba.sk/studium/efm/diplomovky/2009/dobak/diplomovka.pdf >
  7. Prednáška 4 : Numerické metódy matematiky I. Dostupný z WWW: <http://fyzikazeme.sk/mainpage/stud_mat/menm/prednaska4.pdf>
  8. Brezová Martina. Choleského metóda. 2006. Bratislava. Dostupný z WWW:< http://www.mtakac.com/aap/ref/brezova.pdf>
  9. Prednáška 5 : Numerické metódy matematiky I. Dostupný z WWW: <http://fyzikazeme.sk/mainpage/stud_mat/menm/prednaska5.pdf>
  10. Wikipedia [online]. 2007, 19.4.2010 [cit. 2010-05-2]. Conjugate gradient method. Dostupné z WWW: <http://en.wikipedia.org/wiki/Conjugate_gradient_method>.
  11. SAAD, Y. Iterative Methods for Sparse Linear Systems. Manchester , 2000. 447 s. Dostupné z WWW: <http://www.stanford.edu/class/cme324/saad.pdf>.
  12. KALTENBACHER, Manfred. Numerical Simulation of Mechatronic Sensors and Actuators. 2nd Edition. Berlin : Springer, 2007. 428 s. ISBN 978-3-540-71359-3.
  13. HULSEMANN, Frank. Parallel Geometric Multigrid ,2008. 44 s. Dostupné z WWW: <http://www10.informatik.unierlangen.de/Publications/Papers/2005/PGM_LNCSE51.pdf>.
  14. GOULD, N.; HU, Y.; SCOTT, J. A numerical evaluation of sparse direct solvers [online]. 2005 [cit. 2010-05-09]. Dostupné z WWW: <ftp://ftp.numerical.rl.ac.uk/pub/reports/ghsRAL200505.pdf>.
  15. MEEKER, David. Finite Element Method Magnetics User’s Manual [online]., 2007, 5.2.2009 [cit. 2010-05-09]. Dostupné z WWW: <http://www.femm.info/Archives/doc/manual42.pdf>.
  16. ŠTEPANOVSKÝ, Michal. Metóda konečných prvkov : Sprievodný materiál k semináru IT Power Knowledge
  17. BRIGGS, William. A Multigrid Tutorial.. 119 s. Dostupné z WWW: <http://www.cfm.brown.edu/people/gk/APMA2821F/mgtut_part1.pdf>.
Zdroj: „http://www.kiwiki.info/index.php?title=Softvérové_balíky_pre_riešenie_veľkých_lineárnych_systémov&oldid=6428“