Spôsobilosť vonkajších krúžkov kuželíkových ložísk v procese výroby
Obsah
Experimentálna časť diplomovej práce bola realizovaná v laboratórnej učebni Fakulty mechatroniky. Laboratórium katedry metrológie a manažérstva kvality je vybavené modernými meracími zariadeniami značky Mitutoyo. V mojej experimentálnej časti som používal meradlá na meranie dĺžok. Tu môžem spomenúť, že v laboratóriu sa na meranie dĺžok nachádzajú napríklad posuvné meradlá, mikrometre, číselníkové odchýlkomery, prípadne snímač Linear Gage spolu so zobrazovacou jednotkou DIGIMATIC, ktorý meria s vysokou presnosťou. S týmto prístrojom sa dá merať až na desatiny mikrometra, čím môžem povedať, že takéto meradlo môže byť použité aj na kalibráciu iných meradiel. Posudzovaným výrobkom v procese výroby bolo kuželíkové ložisko, presnejšie vonkajší krúžok tohto ložiska. Kuželíkové ložisko je bližšie popísane v kap. 5.1. Meradlá, ktorými som zisťoval príslušne parametre tohto výrobku sú podrobnejšie popísane v kap. 5.2.
5.1 Jednoradové kuželíkové ložiská Kuželíkové ložiská (obr. 11) sú konštrukčne navrhnuté tak, aby umožňovali súčasne pôsobenie radiálneho a axiálneho zaťaženia.[45] Jednoradové kuželíkové ložiská majú jeden rad kuželíkov, ktoré sa funkčným čelom opierajú o vodiaci nákružok vnútorného krúžku.[46] Tieto ložiská sa skladajú z masívneho vonkajšieho a vnútorného krúžku s kužeľovými dráhami a klietok s kuželíkmi.[47] Spravidla majú rozoberateľnú konštrukciu, čiže vnútorný krúžok s klietkou a kuželíkmi tvoria celok, ktorý sa dá montovať nezávisle na vonkajšom krúžku.[48] Výhody kuželíkových ložísk sú[45]:
- významne redukované trenie,
- zvýšená únosnosť,
- vzájomne spoľahlivé nastavenie ložísk,
- zreteľné zlepšenie prevádzkovej spoľahlivosti,
- možnosť pracovať aj pri vysokom zaťažení alebo zošikmení.
[[Súbor:mp_dp_11.jpg|framed|center|Obr. 11 Kuželíkové ložisko]
Konštrukcia a výroba kuželíkových ložísk je na vysokej technickej úrovni. Klzné plochy sú navrhnuté tak, aby sa prívod maziva a tvorba mazivového filmu uľahčil. Optimálnym rozložením tlaku po šírke obežnej dráhy napomáha tvorbe mazivového filmu a k správnemu pohybu kuželíkov. Výsledkom je potom výrazná redukcia trenia, vyššia únosnosť či zlepšenie prevádzkovej spoľahlivosti.[48] Jednoradové kuželíkové ložiská majú uplatnenie v celom rade odvetví. Používajú sa najmä vo výrobe osobných automobilov, ale i nákladných automobilov, traktorov, poľnohospodárskej technike, valcovaných stolíc, zemných strojov, obrábacích strojov, i ako železničné ložiskové jednotky pre nápravy koľajových vozidiel.[49]
Jednoradové kuželíkové ložiská sa bežne vyrábajú v normálnom stupni presnosti P0. Ak ide o zvláštne prípady uloženia, ktoré sú náročné na presnosť alebo pracujú s vysokou frekvenciou otáčania sa sú ložiská vyrábané vo vyššom stupni presnosti P6 a P5, prípadné P4, P2, SP, UP, pričom klesajúce číslo nám označuje vyššiu presnosť. [46] V mojej praktickej časti budem posudzovať spôsobilosť kuželíkového ložiska pre vyšší stupeň P6X aj pre základný stupeň presnosti P0.
Použité meradlá
Na meranie vonkajšieho priemeru krúžku som použil digitálne posuvné meradlo a na meranie šírky vonkajšieho krúžku kuželíkového ložiska som použil číselníkového odchýlkomer.
Posuvné meradlo
Posuvné meradlá sú jednoduché ručné meradlá pre zisťovanie dĺžkových rozmerov súčiastok. Posuvnými meradlami je možné merať vonkajšie i vnútorné rozmery, hĺbky či odsadenia. Štandardné posuvné meradlo využíva princíp nónia pre delenie stupnice.
Hlavné rozmery a konštrukcia posuvných meradiel sú určené normami. Rozsah stupnice meradiel býva rôzny. Vyrábajú sa prevažne v rozmedzí od (0-100) mm až po (0-4000) mm. Posuvné meradlo sa skladá z dvoch hlavných častí:
- pevnej obdĺžnikovej prípadne rúrkovej časti s hlavnou milimetrovou stupnicou a pevnou čeľusťou,
- pohyblivej časti s čeľusťou a nóniovou stupnicou.
Od osemdesiatych rokov sa začali používať digitálne posuvné meradlá (obr. 12), kde nónius nahradil inkrementálny snímač a číslicový displej (najčastejšie s rozlíšením 0,01 mm).
Posuvné meradlá sa vyrábajú obvykle z nelegovaných alebo antikorových ocelí. Čeľuste sú vysoko tvrdené. Tolerancia rovinnosti a priamosti meracích plôch dosahuje 10 µm, rovnobežnosť je v tolerancii 15 µm. Na kalibrovanie sa najčastejšie používajú základné rovnobežné mierky. Pri meraní najčastejšie vznikajú chyby spôsobené nedokonalým dotykom meracích a meraných plôch, nesprávnou polohou meradla, opotrebovaním alebo nepresnou výrobou plôch čeľustí prípadne nepresným odčítaním hodnoty, ktorá vytvára tzv. paralaxnú chybu.[50]
Číselníkový odchýlkomer
Číselníkové odchýlkomery (obr. 13) sú jednoduché meracie prístroje, pre presné odmeriavanie malých vzdialeností. Existujú viaceré typy odchýlkomerov s ozubeným, pákovým, pružinovým či kombinovaným prevodom. Tiež sa rozlišujú odchýlkomery s jednootáčkovým, viacotáčkovým či menej ako jednootáčkovým číselníkom.
Keďže odchýlkomery vyvodia len malý pohyb, používajú sa najčastejšie na komparačné meranie. V spojení s tuhým meracím stojanom je možné vykonávať porovnávacie meranie, a teda takáto zostava slúži ako tzv. komparátor. Nula na stupnici je presúvateľná, preto je možné nastaviť relatívnu nulu v ktorejkoľvek polohe dotyku.
Najbežnejšie je možné sa stretnúť s odchýlkomermi s najmenším dielikom rovným 0,01 mm. Vyrábajú sa však aj odchýlkomery s presnosťou 0,001 mm a aj presnejšie.
Voľba vhodného parametru vonkajšieho krúžku
Na ložisko pôsobí množstvo činiteľov ako napríklad vibrácie, korózia, rôzne montážne chyby, poškodenie klietky, odlupovanie povrchu. Tieto činitele sú príčinami poškodenia ložísk, a v mnohých prípadoch i úplnému vyradeniu z prevádzky. Okrem poškodenia ložiska môže dôjsť aj k poškodeniu iného zariadenia, napríklad časti stroja, v ktorých sa toto ložisko využíva. Preto treba týmto činiteľom predchádzať. Predovšetkým to je čo najpresnejšou výrobou a následnou kontrolou tolerancií.[51]
Presnosť výroby je naozaj dôležitým faktorom, o čom som sa presvedčil aj sám pri experimentálnej časti tejto diplomovej práce. Dovolené odchýlky sa tu pohybovali v rozmedzí niekoľkých mikrometrov. Dovolím si však povedať, že presnosť výroby je dôležitá nielen pri ložiskách, ale všeobecne pri každom vyrábanom výrobku aj keď samozrejme nie vždy v takých malých toleranciách.
Ako som už spomenul, v mojej diplomovej práci som zisťoval spôsobilosť vonkajšieho krúžku kuželíkoveho ložiska. Preto bolo potrebné si zvoliť vhodný parameter tohto krúžku. Za hlavný parameter kvality boli v mojom prípade zvolené dva parametre, a to šírka a priemer vonkajšieho krúžku. Tak ako ostatné aj tieto parametre sú dôležité, pretože napríklad nedodržaním šírky môže dôjsť k únave materiálu spôsobenej nevhodným utesnením telesa ložiska. Parametrom alebo znakom kvality bude teda šírka a priemer krúžku. Aby boli splnené kritéria kvality, čiže aby výrobok spĺňal požiadavky, mali by sa tieto parametre nachádzať v tolerančných medziach, čiže proces by mal byť spôsobilý. Splnenie alebo nesplnenie týchto kritérií sa pokúsim zistiť v ďalšej časti diplomovej práci.
Zhromažďovanie údajov
Meranie a zisťovanie kvality teda prebiehalo v laboratórnej učebni vybavenej potrebnými meradlami. Ako som spomenul, na zbieranie údajov boli použité dva druhy meradiel. V každom výbere sa uskutočnilo 5 meraní pričom celkový počet bol 20 výberov. Hodnoty meraní boli zapisované na hárok a prepísane do prehľadnej tabuľkovej podoby v MS Excel, kde boli uskutočnené potom aj ďalšie výpočty. Boli to hlavne výpočty priemerných hodnôt a rozpätí jednotlivých výberov, ktoré boli využité pri tvorbe regulačných diagramov.
Šírka vonkajšieho krúžku kuželíkového ložiska
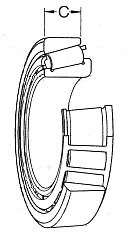
Na meranie šírky vonkajšieho krúžku (obr. 14) som použil číselníkový odchýlkomer.
Tento odchýlkomer má podľa technických údajov (tab. 2) merací rozsah 1 mm, to znamená, že namerané hodnoty, ktoré sú v prílohe A, by sme nemohli dosiahnuť použitím len tohto meradla. Keďže je nula na stupnici odchýlkomera presúvateľná, odmerali sme šírku pomocou mikrometra a zvolili sme si etalónovu hodnotu 11,90 mm ako relatívnu nulu, od ktorej sme potom mohli zisťovať hodnoty už aj pomocou odchýlkomera. Namerané hodnoty šírky krúžku sú v prílohe A.
| Meradlo | č. | Rozsah merania [mm] | Delenie stupnice [mm] | Teplota prostredia [oC] |
| Číselníkový odchýlkomer | 2110 SB-10 | 1 | 0,001 | 23,0 |
Priemer vonkajšieho krúžku kuželíkového ložiska
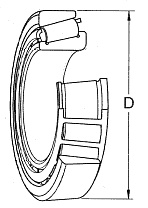
Na meranie priemeru krúžku (obr. 15) bolo použité digitálne posuvné meradlo. Namerané hodnoty priemeru krúžku ložiska sa nachádzajú v prílohe B.
Základné technické údaje digitálneho meradla použitého na meranie priemeru vonkajšieho krúžku, sú popísane v nasledujúcej tabuľke (tab. 3).
| Meradlo | č. | Rozsah merania [mm] | Delenie stupnice [mm] | Teplota prostredia [oC] |
| Posuvné meradlo | 500-181-21 | 0 - 150 | 0,01 | 23,0 |
Analýza spôsobilosti vonkajšieho krúžku ložiska
Po zhromaždení všetkých údajov, môžeme prejsť k analýze týchto údajov a k zisťovaniu spôsobilosti vonkajšieho krúžku pre kuželíkové ložiská.
Histogramy pre zvolené parametre
Začal by som zisťovaním, či dáta, teda namerané údaje pochádzajú z normálneho rozdelenia. K tomu nám pomôže test normality. Keďže však máme hodnoty, ktoré sú rozdelené do podskupín, teda výberov, dokážeme proces vyhodnotiť aj bez testu normality. Ako prvý krok k analýze spôsobilosti teda začnem tvorbou histogramov. Pomocou histogramu môžeme zistiť rozdelenie početností údajov z tabuľky, čo môže byť pre nás užitočné, pretože máme vizuálnu predstavu o predbežnom odhade spôsobilosti procesu.
Namerané hodnoty z tabuľky som spracoval v programe Minitab. Tento program nám na základe vložených údajov umožní zobraziť výstup vo forme histogramu.
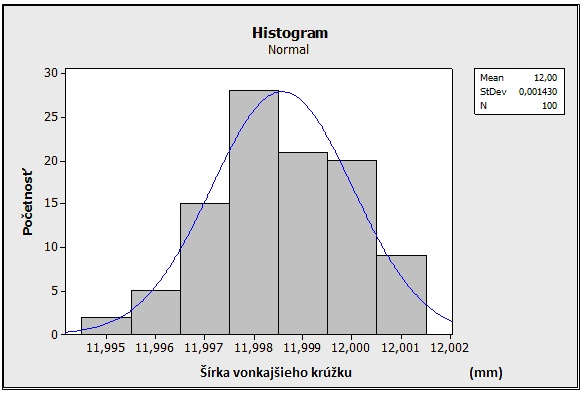
Histogram šírky vonkajšieho krúžku
Z histogramu pre šírku vonkajšieho krúžku (obr. 16) vidíme, že tvar má normálne rozdelenie, čiže namerané hodnoty sú z normálneho rozdelenia a nemáme žiadne vybočujúce meranie.
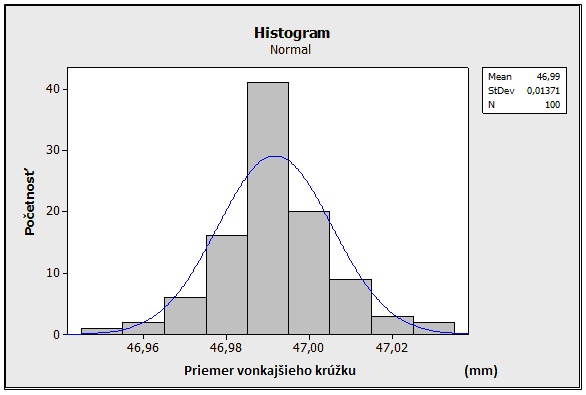
Histogram priemeru vonkajšieho krúžku
Podobne aj histogram pre priemer vonkajšieho krúžku (obr. 17) vykazuje tvar zodpovedajúci normálnemu rozdeleniu. Taktiež ani pri priemere vonkajšieho krúžku nemáme vybočujúce meranie.
Takže pomocou histogramu môžeme zistiť, či sa súbore hodnôt nenachádzajú hodnoty, ktoré by mohli nepriaznivo ovplyvniť proces, čo by sa nám grafickom výstupe zobrazilo. Máme teda vizuálny prehľad o nameraných údajoch.
Keďže z histogramov vidieť, že nemáme hodnoty, ktoré by boli nepriaznivé a bolo by ich treba preskúmať, môžeme ďalej pokračovať v analýze. Histogramom sme získali prvú predstavu o spôsobilosti procesu, nie však nevyhnutne aj o jeho potenciálnej spôsobilosti, lebo príslušne rozdelenie môže byť ovplyvnené vymedziteľnými príčinami. Na to nám slúžia regulačné diagramy.
Regulačné diagramy zvolených parametrov
Teraz budeme teda pomocou regulačných diagramov zisťovať či je proces v štatisticky zvládnutom stave. Pomocou normy ISO 8258 budeme postupovať pri tvorbe regulačných diagramov. Vzhľadom na to, že sme merali hodnoty šírky a priemeru krúžku ložiska použijeme regulačné diagramy na reguláciu meraním. Ako najvhodnejšie regulačné diagramy som si zvolil regulačný diagram pre priemer a regulačný diagram pre rozpätie.
Pre tvorbu týchto regulačných diagramov je potrebné zistiť okrem priemernej hodnoty a rozpätí jednotlivých podskupín aj priemer z jednotlivých priemerov a celkové priemerné rozpätie z jednotlivých rozpätí. Tie sú potrebné na výpočet hornej a dolnej regulačnej medze. Pre ich výpočet použijeme tabuľku z normy ISO 8258 (tab. 4).
| Štatistika | Základné hodnoty nie sú stanovené | |
| Centrálna priamka | UCL a LCL | |
| [math]\overline{X}[/math] | [math]\overline{\overline{X}}[/math] | [math]\overline{\overline{X}}\pm {{A}_{2}}\overline{R}[/math] |
| R | [math]\overline{R}[/math] | [math]{{D}_{4}}\overline{R},\quad {{D}_{3}}\overline{R}[/math] |
Okrem týchto vzorcov sú potrebné aj hodnoty pre súčinitele na výpočet priamok regulačných diagramov. Tieto hodnoty sa taktiež nachádzajú v norme ISO 8258. Keďže hodnoty boli merané v 5 podskupinách, vyberiem iba potrebné súčinitele (tab. 5), kde sú hodnoty zaznamenané iba pre tento rozsah podskupiny.
| Rozsah podsku-piny n | Súčinitele pre regulačné medze | Súčinitele pre centrálnu priamku | ||
| A2 | D3 | D4 | d2 | |
| 5 | 0,577 | 0,000 | 2,114 | 2,326 |
Regulačné diagramy pre šírku vonkajšieho krúžku
Celkový priemer z priemerov jednotlivých podskupín a priemer z rozpätí podskupín sa nachádza v prílohe (príloha A). Pri zisťovaní regulačných medzí teda použijem vzorce a súčinitele použité v tabuľkách (tab. 4), (tab. 5). Prvým krokom bude výpočet medzí a následne zostrojenie R-diagramu a zhodnotenie jeho stavu.
Medze pre R-diagram sú:
Centrálna priamka (CL) = [math]\overline{R}[/math] = 0,0038 mm
Horná medza (UCL) = [math]{{D}_{4}}\overline{R}[/math] = 2,114 . 0,0038 = 0,008 mm
Dolná medza (LCL) = [math]{{D}_{3}}\overline{R}[/math] = 0 . 0,0038 = 0 mm
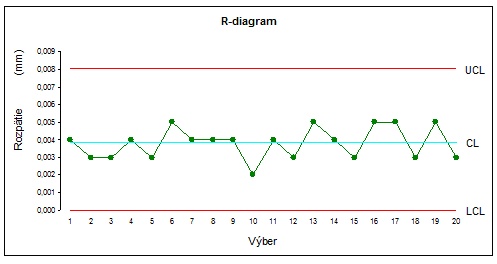
R-diagram pre šírku vonkajšieho krúžku je na obrázku (obr. 18). Môžeme vidieť, že hodnoty sa nachádzajú vo vnútri regulačných medzí, R-diagram nám zobrazuje štatistický zvládnutý stav.
Hodnoty [math]\overline{R}[/math] teraz môžem použiť k výpočtu medzí diagram priemerov.
Medze pre X-diagram sú: Centrálna priamka (CL) = [math]\overline{\overline{X}}[/math] = 11,99857 mm
Horná medza (UCL) = [math]\overline{\overline{X}}+{{A}_{2}}\overline{R}[/math] = 11,99857 + 0,577 . 0,0038 = 12,0008 mm
Dolná medza (LCL) = [math]\overline{\overline{X}}-{{A}_{2}}\overline{R}[/math] = 11,99857 - 0,577 . 0,0038 = 11,9964 mm
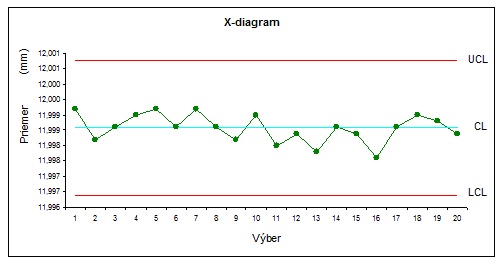
Z obrázka (obr. 19) pre X-diagram vidíme, že žiadne hodnoty sa nenachádzajú mimo regulačných medzí ani sa tu nenachádza žiadne zvláštne zoskupenie bodov, ktoré by bolo preskúmať, môžem povedať, že proces je štatistický zvládnutý a pristúpiť k zisťovaniu spôsobilosti procesu.
Regulačné diagramy pre priemer vonkajšieho krúžku
Celkový priemer z priemerov jednotlivých podskupín a priemer z rozpätí podskupín sa nachádza v prílohe (príloha B). Pri zisťovaní štatistického stavu pre priemer krúžku budeme postupovať rovnakým spôsobom ako to bolo aj v prípade šírky krúžku. Najprv si zistíme regulačné medze pre R-diagram, spravíme grafický výstup a potom pristúpime k zisťovaniu medzí pre X-diagram spolu s grafickým výstupom. Medze pre R-diagram sú:
Centrálna priamka (CL) = [math]\overline{R}[/math] = 0,0345 mm
Horná medza (UCL) = [math]{{D}_{4}}\overline{R}[/math] = 2,114 . 0,0345 = 0,0729 mm
Dolná medza (LCL) = [math]{{D}_{3}}\overline{R}[/math] = 0 . 0,0345 = 0 mm
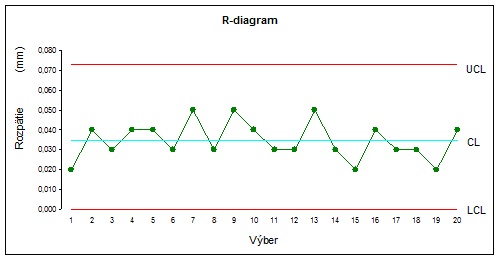
Regulačný diagram rozpätí pre priemer vonkajšieho krúžku kuželíkového ložiska (obr. 20) nám podobne ako v prípade šírky krúžku ukazuje, že hodnoty sa nachádzajú v stanovených medziach, ani sa nám tu nevyskytuje žiadna anomália, preto môžeme pokračovať v zisťovaní medzí a zostrojení X-diagramu.
Medze pre X-diagram sú:
Centrálna priamka (CL) = [math]\overline{\overline{X}}[/math] = 46,9917 mm
Horná medza (UCL) = [math]\overline{\overline{X}}+{{A}_{2}}\overline{R}[/math] = 46,9917+ 0,577 . 0,0345 = 47,0116 mm
Dolná medza (LCL) = [math]\overline{\overline{X}}-{{A}_{2}}\overline{R}[/math] = 46,9917- 0,577 . 0,0345 = 46,9711 mm
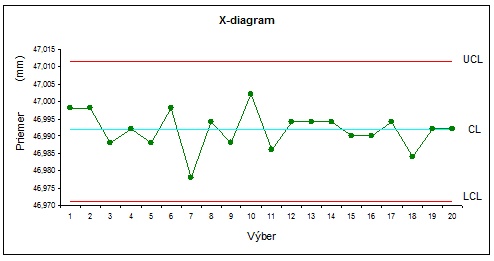
Aj z X-diagramu (obr. 21) môžeme vyčítať, že hodnoty sa nachádzajú v regulačných medziach, čiže aj priemer vonkajšieho krúžku ložiska sa nachádza v štatisticky zvládnutom stave.
Regulačné diagramy môžeme teda používať ako nástroj na monitorovanie procesu alebo aj ako nástroj na sledovanie efektov zmien v procese na jeho spôsobilosť. Analýza spôsobilosti pomocou regulačných diagramov nám môže indikovať, či sa proces dostal to štatisticky nezvládnutého stavu. Vtedy je odhadovať spôsobilosť procesu nebezpečné. Proces musí byť stabilný, aby sme mohli získať spoľahlivý odhad spôsobilosti procesu. Pokiaľ je nestabilný, je prioritou nájsť a eliminovať vymedziteľné príčiny variability.[31] V mojom prípade regulačné diagramy ukázali, že proces je v stabilnom stave a preto môžem prejsť na zisťovanie spôsobilosti.
(5.5.3)