Metrológia, meranie, chyby a neistoty v meraní

|
Trenčianska Univerzita Alexandra Dubčeka v Trenčíne
Fakulta Mechatroniky |

|
Metrológia, meranie, chyby a neistoty v meraní Diplomová práca |
| Autor: | Bc. Michal Páleník |
| Pedagogický vedúci: | Prof. Ing. Michal Obmaščík, Csc. |
| Študijný odbor: | Manažérstvo kvality produkcie |
| Akademický rok | 2009/2010
|
Obsah
V súčasnosti neustále narastajú požiadavky na kvalitu výrobkov, služieb a procesov. Konkurencia sa vo všetkých oblastiach zostruje, preto sa kvalita výrobku stáva rozhodujúcim atribútom úspešného pôsobenia na trhu. V systémoch riadenia kvality tvorí nezanedbateľnú zložku otázka metrologického zabezpečenia. Týka sa hlavných činností organizácií zabezpečujúcich poskytovanie služieb alebo výrobu výrobkov. Väčšina údajov totiž pochádza z meraní, napriek tomu sa tejto problematike často nevenuje dostatočná pozornosť [12].
Metrológia
Metrológia sa zaoberá meraním, meracími jednotkami, metódami a prostriedkami merania a tiež zásadami spracovania výsledkov meraní, s cieľom zabezpečenia jednotnosti a správnosti meraní v rôznych oblastiach ľudskej činnosti [13]. Metrológia patrí medzi činnosti, ktoré sú z pohľadu kvality a technického rozvoja pre priemysel ale i iné oblasti dôležité. Metrológiu v systéme riadenia kvality treba chápať ako súbor činností, ktoré sú spojené s udržovaním, evidenciou, kalibráciou a overovaním meradiel. [14]
Hlavnou náplňou metrológie sú [15]:
- Meracie jednotky na zabezpečenie jednotnosti a presnosti meradiel a merania
- Meranie – meracie postupy a metódy merania, teória chýb a neistôt merania, spracovania výsledkov merania, hodnotenie a analýza výsledkov merania
- Meradlá – hodnotenie ich základných vlastností a funkcií
- Pozorovatelia, t.j. pracovníci, ktorí vykonávajú meranie a ich vplyv na meranie
Meranie
Meranie je neodmysliteľnou súčasťou dneška i budúcnosti, meranie zasahuje do všetkých oblastí hospodárstva. Spomeniem výrok lorda Kelvina o meraní, ktorá hovorí: „... ak viete merať to, o čom hovoríte, a viete to vyjadriť v číslach, potom o tom niečo viete. Keď to však neviete merať, a neviete to vyjadriť číselne, vaša znalosť o tom je chabá a nedostatočná...“
Meranie je súčasťou širokého vedného a technického odboru metrológia.
Cieľavedomé riadenie je možné len tak, kde máme k dispozícii dostatočné množstvo objektívnych poznatkov, a tieto je možné získať iba meraním.[15] Norma STN 01 0115:2001 definuje meranie takto: „meranie je súbor činností s cieľom určiť hodnotu veličiny.“[16] Fyzikálna definícia hovorí, že merať nejakú veličinu znamená určiť jej veľkosť (hodnotu) vo zvolených jednotkách, t.j. zistiť počet týchto jednotiek, obsiahnutých v meranej veličine.[17] Podľa tejto definície je meranie predovšetkým porovnávacím úkonom, kde dve veličiny toho istého druhu porovnávame vo zvolených jednotkách.[15]
To znamená, že cieľom merania je určenie hodnoty meranej veličiny, teda hodnoty určitej veličiny, ktorá sa má merať. Meranie sa preto začína príslušnou špecifikáciou meracej metódy a postupu merania.
Postup merania predstavuje súhrn operácií, ktoré sú osobitne opísané a ktoré sa využívajú na vykonanie konkrétneho merania podľa danej metódy.[18] Meranie nie je nikdy konečným cieľom, ale je prostriedkom na dosiahnutie iných cieľov, pre poznanie a rozhodovanie.[19] Dôležité je ešte spomenúť dva pojmy, ktoré sa pri meraní vyskytujú. Je to presnosť a správnosť merania. Presnosť merania je tesnosť zhody medzi hodnotami veličiny získanými opakovanými meraniami veličiny za špecifických podmienok. Zvyčajne sa vyjadruje číselne pomocou miery nepresnosti, napríklad pomocou smerodajnej odchýlky, rozptylu alebo variačného koeficientu za špecifických podmienok merania.[20] Presnosť obsahuje stupeň zhody s etalónom. Presnosť sa vzťahuje ku kvalite výsledku a odlišuje sa od správnosti, ktorá sa vzťahuje ku kvalite operácie, pomocou ktorej sa dosiahne výsledok. Môže sa stať, že na dosiahnutie výsledku treba zmeniť zariadenie alebo postup. Tento prípad nastáva, ak sa požaduje vyšší stupeň presnosti, ako sa dá dosiahnuť pomocou práve používaného zariadenia alebo metódy.[18] Adekvátnou presnosťou rozumieme priblíženie sa výsledku merania ku konvenčne pravej hodnote v miere, ktorá zodpovedá potrebám a účelu, na ktorý sa ma výsledok merania použiť.[19]
Správnosť predstavuje stupeň zjemnenia pri vykonávaní nejakej operácie alebo stupeň dokonalosti zariadení a metód, ktoré sa používajú na dosiahnutie výsledku. [18]
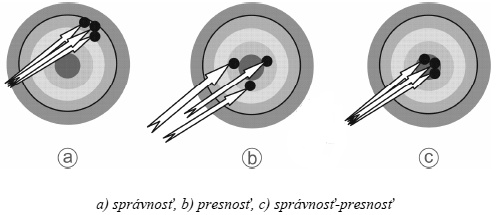
Rozdiel medzi presnosťou a správnosťou si môžeme pozrieť na nasledujúcom obrázku (obr. 3)
Jednoduchšie povedané správnosť súvisí s tým, ako sa meranie (namerané hodnoty) zhodujú so skutočnou meranou hodnotou, zatiaľ čo presnosť súvisí s tým, ako sa opakované merania (namerané hodnoty) zhodujú medzi sebou.[21]
Meranie je teda proces, pri ktorom sa experimentálne získavajú informácie o veľkosti veličiny. [20] Pri opakovanom meraní za rovnakých podmienok však zistíme, že výsledky sa od seba viac alebo menej odlišujú.[14] To znamená že meranie je zaťažené chybou. Tejto problematike sa bližšie venuje nasledujúca podkapitola.
Chyby merania
Pri opakovaní merania tej istej veličiny spravidla dostávame rôzne hodnoty. To znamená, že meriame s určitou nepresnosťou, výsledok merania je teda zaťažený chybou. Preto nedokážeme určiť skutočnú hodnotu meranej veličiny. K skutočnej hodnote sa blížime tým viac, čím viac toto meranie uskutočňujeme. Nepresnosť takéhoto merania môže byť spôsobená nepresným meracím prístrojom, ľudskou chybou, či vplyvom prostredia ako tlak, vlhkosť, teplota a iné. Keďže sa nedá zistiť skutočná hodnota veličiny, používa sa konvenčne pravá hodnota. [15]
Chyba merania je rozdiel medzi nameranou a pravou (skutočnou) hodnotou meranej veličiny. Skutočnú hodnotu meranej veličiny však obyčajne nepoznáme. Matematické vyjadrenie [15]
|
[math]\Delta ={{x}_{n}}-{{x}_{s}}[/math] |
(2.1) |
kde
- Δ je absolútna chyba merania (m),
- [math]x_n[/math] je nameraná hodnota (m),
- [math]x_s[/math] je skutočná hodnota meranej veličiny (m).
Relatívna chyba merania je podiel chyby merania a skutočnej hodnoty meranej veličiny. Matematické vyjadrenie [15]
|
[math]\delta =\frac{\Delta }{{{x}_{s}}}[/math] |
(2.2) |
kde
- δ je relatívna chyba merania,
- Δ je absolútna chyba merania (m),
- [math]x_s[/math] je skutočná hodnota meranej veličiny (m).
Zdroje chýb merania
Ako som už spomínal, výsledky merania môže sprevádzať celý rad nepresností, ktoré sú zdrojmi chýb merania. Medzi najdôležitejšie zdroje chýb merania patria [20]:
- prístrojové chyby – sú chyby vyplývajúce z nedokonalosti použitých meracích prostriedkov. Časť chýb vznikajúcich pri výrobe (napríklad výrobné odchýlky jednotlivých dielov, nepresnosti montáže) sa tiež pri výrobe odstraňuje (napr. justovaním),
- chyby inštalácie – sú chyby vyplývajúce z nedostatkov zapojenia, uloženia a nastavenia meradiel, zo vzájomného ovplyvňovania meradiel zapojených paralelne alebo sériovo, chyby vyplývajúce z ovplyvnenia hodnôt meranej veličiny meradlom a pod.,
- chyby metódy – sú chyby vyplývajúce z nedokonalosti použitých meracích metód, z použitia približných hodnôt fyzikálnych konštánt a nie presne zodpovedajúcich závislostí
- chyby pozorovacie – sú chyby spôsobené nedokonalosťou pozorovateľa
- chyby výpočtové – sú chyby vznikajúce spracovaním nameraných hodnôt (použitie približných vzťahov, chyby interpolácie, extrapolácie, linearizácie a pod.)
Medzi zdroje chýb môžeme zaradiť aj vplyv prostredia, kde ide obzvlášť o chybu spôsobenú teplotou, ďalej to môžu byť vplyvy ako vlhkosť, prašnosť, tlakom vzduchu, svetelným zdrojom, šumom a podobne.[22]
Rozdelenie chýb merania
Chyby merania sa rozdeľujú podľa vplyvu na výsledok merania na:
- chyby náhodne
- chyby systematické
Okrem týchto dvoch druhov chýb existujú ešte aj hrubé chyby. Tie vznikajú nedbalosťou pozorovateľa, takže týmto chybám sa môžeme vyhnúť dôsledným vykonávaním meraní. [20]
Náhodné chyby
Ako z názvu vyplýva náhodne chyby sú spôsobené náhodnými vplyvmi. To znamená, že pri opakovanom meraní tej istej veličiny dostaneme rôzne hodnoty. To môže byť zapríčinené meracím prístrojom, chybou obsluhy alebo prostredím. Tieto hodnoty majú meniace znamienko.[15] Náhodne chyby nemôžeme odstrániť, môžeme ich však zmenšiť opakovaným meraním.[18]
Ako výsledok merania používame aritmetický priemer, ktorý sa najviac približuje k skutočnej hodnote meranej veličiny. Matematické vyjadrenie [20]
|
[math]\bar{x}=\frac{1}{n}\sum\limits_{i=1}^{n}{{{x}_{i}}}[/math] |
(2.3) |
kde
- [math]\bar{x}[/math] je aritmetický priemer (m),
- n je počet opakovaných meraní,
- [math]x_i[/math] je nameraná hodnota (m).
Okrem aritmetického priemeru sa používa v štatistických metódach aj rozptyl, ktorý sa väčšinou charakterizuje smerodajnou odchýlkou. Matematické vyjadrenie
|
[math]s=\sqrt{\frac{\sum\limits_{i=1}^{n}{{{\left( {{x}_{i}}-\bar{x} \right)}^{2}}}}{n-1}}[/math] |
(2.4) |
kde
- s je smerodajná odchýlka (m).
Smerodajná odchýlka nám charakterizuje rozptýlenie výsledkov merania. Hodnota smerodajnej odchýlky však nie je hodnota chyby, vyjadruje hranicu, ktorú náhodná chyba s danou pravdepodobnosťou nesmie prekročiť. Toto už súvisí s neistotou merania.[20] Tú si rozoberieme v ďalšej podkapitole
Systematické chyby
Systematické chyby, sú chyby, ktorých hodnota sa pri rovnakých podmienkach nemení. Majú teda kladnú alebo zápornú hodnotu. Systematické chyby deformujú výsledky určitým pravidelným spôsobom, preto sa snažíme ich zdroje, resp. prejavy eliminovať. Sú to napr. chyby prístrojov, ktoré spôsobujú, že meriame sústavne väčšiu alebo sústavne menšiu hodnotu.[20] Hlavným cieľom je vylúčiť systematickú chybu z výsledku merania. V súvislosti vplyvu systematických chýb na výsledok merania sú zavedené pojmy[15]:
- nekorigovaný výsledok merania
- korigovaný výsledok merania
Nekorigovaný výsledok merania je výsledok merania pred korekciou systematickej chyby a korigovaný výsledok merania po korekcii systematickej chyby. Korekcia je záporná hodnota známej časti systematickej chyby, ktorá sa musí algebraicky pripočítať k nekorigovanému výsledku merania. Systematické chyby sa nedajú presne zistiť a preto sa delia na systematické chyby:
- známe (majú určitú hodnotu a znamienko a je ich možné odstrániť korekciou)
- neznáme (nemajú určité znamienko a zahŕňame ich do neistoty merania).[15]
Teoreticky sa systematické chyby dajú rozdeliť na dva typy[15]:
- aditívne – ich hodnoty zostávajú konštantné v celom rozsahu merania.
- multiplikatívne – ich hodnoty sú na hodnote meranej veličiny závislé, menia sa
Systematické chyby sa snažíme zistiť a odstrániť nasledujúcim spôsobom[20]:
- odstránením príčin, ktoré ich vyvolávajú
- vhodnou kompenzáciou
- uplatnením príslušných korekcií
- kombináciou uvedených spôsobov
Zisťovanie a odstraňovanie systematických chýb je náročné a nákladné a preto sa realizuje len tam kde je to nevyhnutné. Možnosť poznania systematickej chyby je obmedzená, nepoznáme totiž jej skutočnú hodnotu ale iba odhad. Pri korekcii teda odstránime odhad systematickej chyby, pričom časť zostáva nevylúčená. Jej veľkosť nepoznáme a nazývame ju nevylúčenou systematickou chybou.[20]
Neistoty v meraní
Definícia pojmu neistota v meraní je, že neistota v meraní je parameter súvisiaci s výsledkom merania, ktorý charakterizuje rozptyl hodnôt, ktoré možno racionálne priradiť k meranej veličine. Hlavné faktory, ktoré prispievajú k neistote sú zdroje neistôt.[20] Neistotu výsledkov meraní spôsobujú náhodne chyby, ako i identifikovateľne a kvantifikovateľne zdroje chýb, ktoré ovplyvňujú výsledok merania.[23] Medzi zdroje neistôt pri meraní patria[20]:
- neúplná definícia meranej veličiny,
- nedokonalá realizácia definície meranej veličiny,
- nereprezentatívny výber vzoriek
- nedostatočne známe účinky podmienok prostredia alebo ich nedokonalé meranie,
- subjektívnosť odčítavania z analógových prístrojov,
- nepresnosť etalónov a referenčných materiálov
- aproximácie a predpoklady zahrnuté v metóde a postupe merania,
- zmeny pri opakovaných meraniach meranej veličiny v rovnakých podmienkach.
Základom určovania neistôt je, že sa vychádza z teórie pravdepodobnosti a matematickej štatistiky. Predpokladá sa, že merané hodnoty podliehajú rozdeleniu pravdepodobnosti.[20]
Základnou kvantitatívnou charakteristikou neistoty je smerodajná odchýlka hodnoty a označuje sa ako štandardná neistota u. Štandardné neistoty môžeme vyhodnocovať dvoma metódami[20]:
- štandardné neistoty typu A, ktoré sa určujú pomocou štatistických metód a sú spôsobené náhodnými vplyvmi
- štandardné neistoty typu B, ktoré sú spôsobené známymi vplyvmi a určujú sa inak ako použitým štatistickým spracovaním
V praxi si málokedy vystačíme iba s jedným alebo iba druhým typom neistoty zvlášť. Preto je potrebné určiť výsledný efekt kombinovaných neistôt merania oboch typov.[24]
Keďže sa teda nedá použiť iba jeden typ neistoty, používa sa kombinovaná neistota, oboch typov neistôt A aj B, pričom jej vzťah môžeme uviesť ako:[15]
|
[math]{{u}_{Cx}}=\sqrt{u_{Ax}^{2}+u_{Bx}^{2}}[/math] |
(2.5) |
Štandardné neistoty vytvárajú interval pokrývajúci skutočnú hodnotu s pomerne malou pravdepodobnosťou. Preto ak chceme vytvoriť interval s pravdepodobnosťou pokrytia skutočnej hodnoty blízkej 100% treba použiť koeficient rozšírenia k. Takáto neistota sa nazýva rozšírená neistota U. Matematické vyjadrenie [15]
|
[math]U=k u[/math] |
(2.6) |
kde
- U je rozšírená neistota (m),
- k je koeficient rozšírenia,
- u je štandardná neistota (m).
Koeficient rozšírenia sa volí podľa požadovaného intervalu. Pre k = 2 je pravdepodobnosť približne 95%, k = 3 je 99,7%.[15]
Vyhodnotenie štandardných neistôt typu A
Vyhodnotenie typu A vychádza zo štatistickej analýzy opakovaných meraní údajov. Príčiny týchto neistôt sú na rozdiel od typu B neznáme. Pre túto metódu je typické, že rastúcim meraním ich hodnoty klesajú. Ak opakujeme meranie veličiny, odhad výslednej hodnoty reprezentuje hodnota výberového (aritmetického) priemeru, ktorý sa vypočíta rovnako ako vo vzťahu (2.3). Štandardná neistota metódou A sa rovná smerodajnej odchýlke výslednej hodnoty, čiže aritmetického priemeru.[15] Matematicky:
|
[math]{{u}_{Ax}}={{s}_{{\bar{x}}}}=\frac{{{s}_{x}}}{\sqrt{n}}=\sqrt{\frac{1}{n\left( n-1 \right)}\sum\limits_{i=1}^{n}{{{\left( {{x}_{i}}-\bar{x} \right)}^{2}}}}[/math] |
(2.7) |
Ak použijeme malý počet opakovaných meraní (n < 10) je hodnota podľa vzťahu (2.14) málo spoľahlivá. Preto použijeme metódu B, ktorá nie je založená na štatistických metódach.[15]
Vyhodnotenie štandardných neistôt typu B
Ako bolo spomenuté, neistoty typu B sú založené na iných ako štatistických prístupoch.[15] Tieto neistoty sa viažu na známe, identifikovateľné zdroje. [20] Odhaduje sa na základe možných dostupných informácii ako sú údaje na meracích prostriedkoch, zistenia z predchádzajúcich meraní, z neistoty referenčných údajov, zo skúsenosti o meranom objekte.[15] Táto metóda na rozdiel od typu A nie je závislá od počtu meraní. Pri neistote typu B vychádzame z čiastkových neistôt jednotlivých zdrojov uBzi. Ak je známa maximálna odchýlka i-teho zdroja neistoty zimax, neistota uBzi sa určí zo vzťahu[15]
|
[math]{{u}_{B{{z}_{i}}}}=\frac{{{z}_{i\max }}}{k}[/math] |
(2.8) |
kde
- k je súčiniteľ vychádzajúci zo zákona rozdelenia,
Ak je hodnota štandardnej neistoty [math]u_{Bzi}[/math] známa, výsledná hodnota pre r zdrojov sa určí podľa vzťahu [15]
|
[math]{{u}_{Bx}}=\sqrt{\sum\limits_{i=1}^{r}{A_{i}^{2}.u_{B{{z}_{i}}}^{2}}}[/math] |
(2.9) |
kde
- [math]u_{Bzi}[/math] sú neistoty jednotlivých zdrojov (m),
- [math]A_i[/math] ich súčinitele citlivosti.