Analyzátor nameraných dát z meracích prístrojov v priemysle

	Trenčianska Univerzita Alexandra Dubčeka v Trenčíne Fakulta Mechatroniky
	Analyzátor nameraných dát z meracích prístrojov v priemysle zadanie práce Ročníková práca

Autor:	Bc. Pavel Hromada
Pedagogický vedúci:	Ing. Michal Štepanovský, PhD
Študijný odbor:	Mechatronika
Akademický rok	2009/2010

Obsah práce

1.	Teória genetických algoritmov
2.	Implementácia genetických algoritmov
3.	Testovacia úloha pre genetický algoritmus

Abstrakt Práca sa zaoberá genetickým algoritmom, opisuje princíp tohto algoritmu, jeho jednotlivé prvky a na ilustratívnych príkladoch ukazuje funkčnosť tohto algoritmu. Úlohou tohto projektu bolo vytvoriť program v ľubovoľnom programovacom jazyku, ktorý nájde aproximujúcu funkciu k nameraným dátam. Tento program pritom využíva genetický algoritmus, presnejšie genetický algoritmus s reálne kódovanými chromozómami.

Abstract This thesis deals with Genetic Algorithm, it describes the principle and individual parts of this algorithm and by using simple examples shows functionality of this algorithm. The task of this project was to develop a program in any programming language, which finds the approximating function to the measured data. This programm is also using the Genetic Algorithm, concretely Real Coded Genetic Algorithm.

Úvod

V súčasnej dobe patria najrôznejšie heuristické metódy založené na darwinowskom princípe evolúcie medzi veľmi populárne a často používané optimalizačné techniky. Každoročne sú organizované desiatky odborných konferencii zaoberajúcich sa problematikou evolučných algoritmov a ich aplikáciou, vychádzajú stovky publikácii a niektorý autori dokonca už začínajú varovať pred prílišnou popularizáciou evolučných techník, ktoré síce na jednej strane priťahujú nových užívateľov, ale na druhej strane nutne vedú k nerealistickým očakávaniam. Pri porovnaní genetického algoritmu s tradičnými optimalizačnými metódami je možné ľahko nájsť niekoľko výrazných odlišností, ktoré významným spôsobom prispievajú k univerzálnosti a robustnosti genetického algoritmu. Prvým zrejmým rozdielom je využitie celej populácie riešení z prehľadávaného priestoru namiesto jediného počiatočného riešenia, ako je to u väčšiny klasických algoritmov. Táto skutočnosť podstatne ovplyvňuje celkovú robustnosť algoritmu a súčasne priamo navádza na paralelizáciu vlastného výpočtu. Genetický algoritmus je slepý algoritmus, pretože okrem ohodnotenia jedincov v populácii nevyužíva žiadnu apriórnu informáciu či vlastnosť, ktorá sa viaže ku konkrétnemu problému alebo prehľadávanému priestoru. To ho na jednej strane robí veľmi všeobecným a univerzálnym, na druhej strane je zrejmé, že práve toto ignorovanie špecifických vlastností konkrétneho problému bude znamenať, že algoritmus bude len ťažko schopný konkurovať špeciálnym algoritmom, ktoré boli navrhnuté priamo pre daný problém.[3] Evolučným algoritmom, konkrétne genetickým algoritmom sa zaoberá aj tento ročníkový projekt. Výsledkom tohto projektu by mal byť počítačový program, ktorý aplikovaním genetického algoritmu nájde vhodnú aproximujúcu funkciu k vopred daným nameraným dátam. Nutné je podotknúť, že túto aproximujúcu funkciu zadá užívateľ programu ako vstup pre algoritmus. Úlohou genetického algoritmu v tomto programe potom teda bude nájsť konštanty vyskytujúce sa v zadanej funkcii tak, aby táto funkcia čo najlepšie aproximovala namerané dáta.

Teória genetických algoritmov

História

Problematika genetických algoritmov respektíve genetické algoritmy ako také sa ešte aj v súčasnosti považujú za mladú disciplínu, ktorá je stále predmetom skúmania a štúdia mnohých profesorov. Sú súčasťou evolučných výpočtov, ktoré patria do prudko sa rozvíjajúcej oblasti umelej inteligencie. Myšlienka evolučných výpočtov bola prvý raz zavedená v roku 1970 v práci I. Rechenberga s názvom Evolučné stratégie (originál Evolutionsstrategie). Táto myšlienka evolučných výpočtov bola ďalej rozvíjaná inými výskumníkmi. Zrod genetických algoritmov sa pripisuje Johnovi Hollandovi, ktorý v roku 1975 vydal knihu Prispôsobovanie sa v prírodných a umelých systémoch (originál Adaption in Natural and Artifiacial Systems). V roku 1992 použil John Koza genetický algoritmus pri vývoji ďalšej oblasti informatiky nazvanej genetické programovanie.

Biologické pozadie genetických algoritmov

Všetky živé organizmy v prírode sa skladajú z buniek. Sú to základné stavebné častice, ktoré sú v jednotlivých organizmoch zložené vždy z rovnakej série chromozómov, pričom sú to určité reťazce DNA a slúžia ako model pre celý organizmus. Ďalej ešte každý chromozóm pozostáva z génov, ktoré predstavujú bloky DNA. Každý gén v sebe nesie určitú informáciu, nazývanú alela. V zásade je možné povedať, že v sebe kóduje konkrétnu črtu. V živých organizmoch touto črtou môže byť napríklad farba očí. Každý gén má v chromozóme svoju vlastnú pozíciu. Táto pozícia sa niekedy označuje ako geometrické miesto génu. Pri ďalšom popise živých organizmov sa stretneme aj s pojmom genóm a genotyp. Genóm je kompletný súbor genetického materiálu (všetky chromozómy) a genotyp predstavuje genetickú informáciu určitej populácie jedincov. [1] V nasledujúcich kapitolách uvidíme, že podobnosť genetických algoritmov s vývojom v živej prírode je veľmi podobný.

Pri vývoji genetických algoritmov sa vychádzalo s Darwinovej teórie evolúcie, ktorá sa zakladá na téze prirodzeného výberu, podľa ktorej prežívajú len najlepšie prispôsobený jedinci populácie. Reprodukciou dvoch silných jedincov dostávame potomkov, ktorý s vysokou pravdepodobnosťou budú dobre prispôsobený k úspešnému prežitiu. Pri podrobnej analýze (hlavne matematickej) sa ukazuje, že samotné pôsobenie reprodukcie nie je dostatočne efektívne na vznik dobre prispôsobených jedincov s novými vlastnosťami, ktoré významne uľahčujú prežitie. Do evolúcie živej hmoty je nutné zapojiť aj tzv. mutácie. Tieto náhodným spôsobom ovplyvňujú (kladne alebo záporne) genetický materiál populácie jedincov. Biologická evolúcia je progresívna zmena obsahu genetickej informácie populácie v priebehu mnohých generácii. V genetických algoritmoch hrá kľúčovú úlohu sila genotypu. V biológii je sila definovaná ako relatívna schopnosť prežitia a reprodukcie genotypu v danom prostredí. Podobe sa chápe aj v umelom živote, je to kladné číslo priradené genetickej informácii reprezentujúcej organizmus (obvykle vyjadrenej pomocou bitového reťazca), ktoré reprezentuje jeho relatívnu úspešnosť plniť si v danom prostredí svoje úlohy (napr. zber potravy) a vstupovať do reprodukcie, t.j. tvoriť nové organizmy.

Biologická evolúcia obsahuje dve základné zložky:

• Prirodzený výber (Darwin) – organizmy s väčšou silou produkujú viac potomkov, ktorí sa dožijú dospelosti a ďalej sa reprodukujú, ako organizmy s malou silou.

• Genetický drift – náhodné udalosti (napr. mutácia alebo náhodná smrť organizmu s veľkou silou prv ako stihol vyprodukovať potomkov) môžu podstatne ovplyvniť evolučné procesy v malých populáciách. [2]

Genetický algoritmus

Ako som už spomenul, genetický algoritmus je založený na myšlienke Darwinovského princípu evolúcie. Hľadanie optimálneho riešenia (respektíve dostatočne vyhovujúceho) prebieha formou súťaže v rámci populácie postupne sa vyvíjajúcich riešení. K tomu, aby bolo možné posúdiť, ktorí členovia populácie majú väčšiu šancu podieľať sa na ďalšom vývoji hľadaného riešenia, musí byť táto schopnosť jedincov kvantifikovaná. V tejto súvislosti sa hovorí o ohodnocovaní, miere kvality, vhodnosti, sile, respektíve reprodukčnej schopnosti jedinca (často sa používa anglický výraz fitness). Jedinci s lepším ohodnotením (vyššou hodnotou fitness) majú prirodzene väčšiu šancu prežiť dlhšie a podieľať sa na vytváraní nasledujúcej generácie. Použitím rozmanitých techník kríženia, mutácie a reprodukcie potom vznikne nová generácia jedincov, v ktorej sú vlastnosti týchto jedincov čiastočne zdedené po rodičoch a čiastočne ovplyvnené náhodnými mutáciami v procese reprodukcie. Ak sa opakuje tento evolučný cyklus niekoľkokrát, obvykle po desiatkach až stovkách opakovaní vznikne populácia s jedincami, ktorí majú vysoké ohodnotenie a môžu predstavovať dostatočné (možno aj optimálne) riešenie daného problému. Pretože tento evolučný proces v sebe zahrňuje značný diel náhodnosti, je zrejmé, že každý beh daného algoritmu sa bude obvíjať odlišným spôsobom. [3]

Tento princíp by sa tiež dal popísať aj trochu inými slovami a o niečo konkrétnejšie. Genetický algoritmus je v podstate postupná tvorba generácii rôznych riešení daného problému. Pri riešení sa uchováva tzv. populácia, ktorej každý jedinec predstavuje jedno riešenie daného problému (konkrétny chromozóm). Tak ako populácia prebieha evolúciou, riešenia sa zlepšujú. Tradične býva riešenie reprezentované binárnymi číslami, reťazcom núl a jednotiek, ale využívajú sa aj iné typy reprezentácie. Typicky je na začiatku procesu genetického algoritmu populácia zložená z náhodných členov. V prechode do novej generácie je každý jedinec ohodnotený fitness funkciou, čo vlastne vyjadruje kvalitu riešenia reprezentovanú týmto jedincom. A následne sú podľa tejto kvality stochasticky vyberané jedince, ktoré sú modifikované (krížením a mutáciou), čím vznikne nová populácia. Tento postup sa opakuje iteratívne, čím sa kvalita populácie postupne vylepšuje. Algoritmus sa obvykle zastaví pri dosiahnutí dostačujúcej kvality riešenia, prípadne po dosiahnutí maximálneho počtu iterácii. [4]

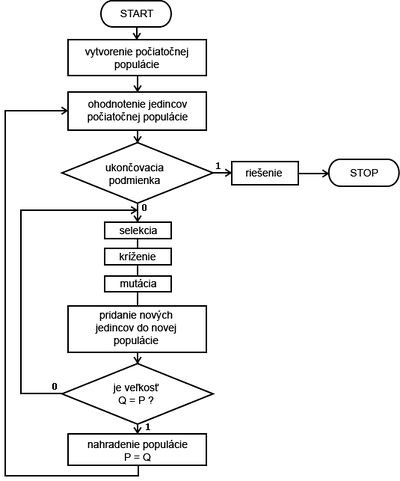
Princíp tohto algoritmu by sa teda dal zapísať nasledovnými krokmi:

1. [inicializácia] Nastav počítadlo na N = 0 a vytvor nultú populáciu jedincov P(N)
2. Spočítaj silu (fitness) jedincov z populácie P(N)
3. [začiatok cyklu] Selekciou respektíve určitou výberovou metódou vyber z populácie niekoľko zdatných jedincov
4. Z týchto jedincov pomocou genetických operátorov vytvor nové, čím vznikne nová generácia
   • Reprodukcia
   • Kríženie
   • Mutácia
5. Spočítaj silu jedincov v novovytvorenej populácii
6. [koniec cyklu] Ak nie je splnená ukončovacia podmienka choď na bod 3
7. [koniec algoritmu] Najzdatnejší jedinec je riešením

Následne je už jednoduché vytvoriť všeobecný pseudo kód genetického algoritmu, ktorý môže vyzerať nasledovne:

N = 0;                      // vynulovanie pocitadla
pociatocna_populacia( P );  // inicializacia pociatocnej populacie
ohodnot( P );               // ohodnotenie jedincov v pociatocnej populacii
while (ukoncovacia_podmienka)
{
    N = N + 1;                      // inkrementuj pocitadlo o 1
    while(Q < P){                   // kým nie je Q rovnako velke ako P
      (x1,x2) = select_from(P);     // vyber 2 zdatne chromozomy x1,x2   P
      (x1‘,x2‘) = crossover( x1, x2 );       // krizenie chromozomov
      (x1‘,x2‘) = mutate( x1‘, x2‘ );          // mutacia chromozomov
      Q = Q  (x1‘,x2‘); //pridanie novych chromozomov do docasnej populacie   
    }
    P = Q;              // nahradenie starej generacie novou	     
    ohodnot( P );       // ohodnotenie jedincov v novej populacii
}

Vonkajší while cyklus sa bude opakovať tak dlho, až kým nebude splnená ukončovacia podmienka. Touto podmienkou pritom môže byť dosiahnutie maximálneho počtu iterácii teda maximálneho počtu vytvorených populácii alebo priblíženiu sa k požadovanej hodnote, ktorú dosahujú chromozómy svojou hodnotou fitness. Vnútorný cyklus while slúži na vytvorenie novej populácie. Opakuje sa dovtedy, kým veľkosť novovytvorenej dočasnej populácie Q a predošlej populácie P nie je rovnaká. V tele tohto cyklu sa vykonávajú operácie genetického algoritmu teda výber zdatných chromozómov, kríženie a mutácia. Následne po týchto operáciách sa novovytvorené chromozómy pridajú do dočasnej populácie Q. Keď tento vnútorný cyklus skončí, pôvodná populácia P bude nahradená novou Q a následne sa ohodnotia jej chromozómy.

Obr. 1.1: Vývojový diagram genetického algoritmu

Ilustratívny príklad princípu genetického algoritmu

V tejto kapitole rozoberiem princíp genetického algoritmu, pričom nebudem rozoberať konkrétny prípad z praxe, ale v niekoľkých krokoch ilustratívne ukážem ako v genetickom algoritme pôsobia genetické operátory, selekcia a ako sa zmení ohodnotenie jednotlivých chromozómov populácie po jednej iterácii takéhoto algoritmu. Pre jednoduchšie pochopenie bude zvolené binárne kódovanie chromozómov.

Vytvorenie počiatočnej populácie:

V tomto prípade bude teda počiatočnú populáciu tvoriť množina náhodne vygenerovaných binárnych reťazcov danej dĺžky. Predpokladajme, že náhodne vygenerovaná populácia sa skladá zo štyroch jedincov, pričom každý z nich je reprezentovaný chromozómom dĺžky 8 nasledovne:

Tab. 1.1: Ukážka náhodne vygenerovanej populácie

Jedinec č.	Chromozóm
1	(1,0,1,0,1,1,0,0)
2	(0,1,1,1,1,0,1,1)
3	(0,0,0,1,0,0,0,1)
4	(1,1,0,0,1,1,0,0)

Ohodnotenie jedincov:

Je zrejmé, že ohodnocujúca funkcia je vždy zviazaná s konkrétnym problémom, pretože cieľom je nájsť takého jedinca respektíve jedincov, ktoré majú z hľadiska príslušného problému čo možno najvhodnejšie vlastnosti. V tomto ilustratívnom príklade bude ohodnocujúca funkcia predstavovať súčet všetkých jednotkových bitov v chromozóme. Priemerné ohodnotenie populácie bude mať hodnotu 4.

Tab. 1.2: Ukážka ohodnotenia jedincov populácie

Jedinec č.	Chromozóm	Ohodnotenie (fi)	% z celku	Kumulovane
1	(1,0,1,0,1,1,0,0)	4	25,0 %	0,250
2	(0,1,1,1,1,0,1,1)	6	37,5 %	0,250
1	(0,0,0,1,0,0,0,1)	2	12,5 %	0,750
4	(1,1,0,0,1,1,0,0)	4	25,0 %	1,000

Výber dvojíc určených k reprodukcii:

Nasledujúci výber jedincov určených k reprodukcii by mal byť imitáciou prirodzeného výberu, ako to popisuje Darwin vo svojej teórii o pôvode druhov. To znamená, že zdatnejší jedinci majú väčšiu šancu prežiť a majú tiež väčšiu pravdepodobnosť byť vybrané na reprodukciu. Selekčné mechanizmy (postupy výberu jedincov) sú popísané v kapitole 1.3.4. V tomto príklade boli k reprodukcii vybrané jedince číslo 2, 3 a 4. Vidno, že najlepšie ohodnotený jedinec bol vybraný dva krát (číslo 2).

Tab. 1.3: Ukážka dvojíc vybraných pre účely reprodukcie

	Jedinec č.	Chromozóm
1.pár	2	(0,1,1,1,1,0,1,1)
	4	(1,1,0,0,1,1,0,0)
2.pár	3	(0,0,0,1,0,0,0,1)
	2	(0,1,1,1,1,0,1,1)

Kríženie:

Princípov kríženia existuje v genetických algoritmoch niekoľko. Podrobnejšie sú rozobrané v kapitole 1.3.5.1. Pre účely tohto príkladu postačí zrejme najjednoduchší druh kríženia a to jednobodové kríženie. Zvolíme teda náhodne jeden gén v chromozóme a od tohto génu vymeníme ostatné časti chromozómu medzi obidvomi rodičmi. Tak vzniknú dvaja nový jedinci, z ktorých každý má časť genetickej výbavy po prvom a časť po druhom z rodičov. V tomto príklade bol vybraný druhý gén ako bod kríženia pre prvý rodičovský pár a štvrtý gén pre druhý pár. Výsledok je potom nasledovný:

Tab. 1.4: Ukážka kríženia rodičovských chromozómov

	Chromozóm		Nový chromozóm
1.pár	(0,1, | 1,1,1,0,1,1)	->	(0,1, | 0,0,1,1,0,0)
	(1,1, | 0,0,1,1,0,0)	->	(1,1, | 1,1,1,0,1,1)
2.pár	(0,0,0,1, | 0,0,0,1)	->	(0,0,0,1, | 1,0,1,1)
	(0,1,1,1, | 1,0,1,1)	->	(0,1,1,1, | 0,0,0,1)

Mutácia:

Mutácia väčšinou veľmi jednoduchým spôsobom a s relatívne malou pravdepodobnosťou mení náhodne hodnotu jednotlivých génov. V prípade binárneho kódovania to znamená zmeniť hodnotu génu z nuly na jednotku respektíve naopak. V tomto príklade môže populácia po mutácii vyzerať nasledovne:

Tab. 1.5: Ukážka mutácie chromozómov vzniknutých krížením

header 1		header 3
(0,1,0,0,1,1,0,0)	->	(0,1,0,1,1,1,0,0)
(1,1,1,1,1,0,1,1)	->	(1,1,1,1,1,0,1,1)
(0,0,0,1, 1,0,1,1)	->	(0,0,0,1, 1,0,1,1)
(0,1,1,1, 0,0,0,1)	->	(0,1,1,1, 0,0,0,0)

Vytvorenie novej populácie:

Ďalším krokom je vytvorenie novej populácie z pôvodnej populácie a množiny potomkov. Ak použijeme najjednoduchšiu tzv. generačnú stratégiu vytvárania novej populácie, ktorá je založená na predpoklade vymretia pôvodnej populácie, stará populácia P(0) stratí už akýkoľvek význam a bude z ďalšieho uvažovania vylúčená (úplne vymrie). Práve vytvorené potomstvo pôvodnej populácie sa stáva novou populáciou P(1), ktorá má v tomto príklade nasledujúcu podobu:

Tab. 1.6: Ukážka zmeny kvality (ohodnotenia) novej populácie

Jedinec č.	Chromozóm	Ohodnotenie
5	(0,1,0,1,1,1,0,0)	4
6	(1,1,1,1,1,0,1,1)	7
7	(0,0,0,1, 1,0,1,1)	4
8	(0,1,1,1, 0,0,0,0)	3

Tým bol dokončený prechod od jednej populácie k druhej a celý cyklus sa bude opakovať tak dlho, pokým nebude splnená ukončovacia podmienka. V novovytvorenej populácii možno vidieť, že ohodnotenie jednotlivých jedincov sa zlepšilo a vzrástlo tiež priemerné ohodnotenie populácie na hodnotu 4,5. [3]

Ohodnocujúca funkcia - Fitness funkcia

Ohodnocujúca funkcia musí byť úzko zviazaná s konkrétnym problémom, ktorý sa pokúšame použitím genetického algoritmu riešiť. Často sa ako ohodnocujúca funkcia používa priamo účelová funkcia respektíve jej vhodná modifikácia tak, aby bolo možné bez veľkých problémov usporiadať všetky potenciálne riešenia z hľadiska ich vhodnosti. Takisto v tejto práci bude použitá priamo účelová funkcia na ohodnotenie jednotlivých jedincov. Znamená to teda, že aproximujúca funkcia, ktorú zadá na vstupe užívateľ aby aproximovala namerané dáta, bude použitá na výpočet ohodnotenia daných jedincov populácie. Na druhej strane je možné ľahko nájsť prípady, kedy takto jednoducho postupovať nejde a bude nutné pristúpiť k inému spôsobu ohodnotenia jedincov. Predpokladajme napríklad, že jedince v populácii reprezentujúce rôzne herné stratégie istej hry. Ak nastane situácia, že stratégia A je lepšia ako stratégia B (to znamená, že pri použití stratégie A vyhráme nad hráčom, ktorý postupuje podľa stratégie B), B je lepšie ako C a C je lepšie než A, dostaneme sa do problémov s ohodnotením príslušných jedincov. Pokiaľ budú všetky jedince ohodnotené rovnakou hodnotou (pretože každá stratégia poráža jednu z dvoch ostatných), strácame informáciu o tom, že pri vzájomnom posúdení ľubovoľnej dvojice stratégii môžeme určiť jasného víťaza príslušného duelu. Pokiaľ naopak zvolená funkcia určí pre tieto tri jedince vzájomne rozdielne ohodnotenie, nutne bude existovať dvojica stratégii, pre ktoré ich ohodnotenie bude v spore s výsledkom ich vzájomného stretnutia v hre. Dôsledkom toho by bol v oboch prípadoch evolučný algoritmus použitou funkciou klamaný. Takto popísaný problém je spôsobený skutočnosťou, že použitá miera vhodnosti neumožňuje určiť absolútne poradie všetkých jedincov, pretože ide o mieru relatívnu, spočívajúcu vo vzájomnom porovnaní alebo súťažení jedincov v danej populácii. Relatívne ohodnotenie jedinca môže byť vypočítané napríklad ako celkový počet víťazstiev pri porovnaní so všetkými ostatnými jedincami v populácii. Pretože tento spôsob vyžaduje prevedenie celkom

[math]\frac{N \cdot (N-1)}{2}[/math]

(6)

Porovnaní, kde N je veľkosť populácie, ide o časovo pomerne náročnú záležitosť a preto boli navrhnuté alternatívne metódy. Celú populáciu je možné napríklad rozdeliť do dvoch rovnako veľkých častí o veľkosti N/2 a potom jedinec pri svojom ohodnotení podstupuje porovnanie iba s jedincami z druhej polovice populácie. Toto riešenie je vo svojej podstate predstupňom koevolúcie, kedy sa paralelne vyvíjajú dve vzájomne súperiace alebo naopak kooperujúce populácie jedincov. Inou cestou je usporiadanie turnaja medzi jedincami, kedy lepší jedinec z každej náhodne vylosovanej dvojice postupuje do ďalšieho kola, kde sa stretne s iným náhodne vybraným víťazom predchádzajúceho kola. Na konci turnaja ostáva jediný víťaz a ostatným jedincom sa priradí hodnota zodpovedajúca ich pôsobeniu v turnaji. Táto metóda so sebou prináša riziko prílišného zjednodušenia, ktorým platíme za veľmi malý počet potrebných porovnaní (stačí vykonať len N-1 porovnaní). Veľmi úspešným je postup populárne nazývaný „sieň slávy“, kedy ohodnocovaný jedinec podstupuje porovnanie s najlepšími jedincami z predchádzajúcej populácie, ktoré postupne vstupujú do testovacej množiny (siene slávy) a celkom logicky predstavujú ťažkých a náročných konkurentov. [3]

Selekcia – výber chromozómov

Ako je už známe, v cykle genetického algoritmu nastáva operácia nazývaná selekcia alebo inak povedané výber rodičovských chromozómov, ktoré sa ďalej zúčastňujú procesu kríženia. Problémom teraz je, ako vybrať tie najvhodnejšie chromozómy z populácie. Vzhliadnuc k Darwinovej evolučnej teórii, podľa ktorého sa zúčastňujú reprodukcie najzdatnejšie jedince, by mal výber chromozómov v genetickom algoritme podliehať tiež týmto pravidlám. Je známych viacero metód, akými môžu byť chromozómy vybrané. Patria sem napríklad ruletové koleso (Roulette Wheel selection), výber podľa poradia (Rank selection), turnajový výber (Tournament selection), Boltzmanov výber alebo niektoré iné. [1]

Ruletové koleso – Roulette wheel

Základom pre princíp ruletového kolesa je ohodnotenie všetkých chromozómov v populácii. Následne sa každému chromozómu priradí taký veľký výsek kolesa, aká je veľkosť sily (fitness) daného chromozómu. Znamená to, že veľkosť výseku, ktorý sa priradí určitému chromozómu je priamo úmerný sile tohto chromozómu a tým pádom má tento chromozóm väčšiu šancu na výber. Slabšie chromozómy majú priradený menší výsek, čo ich síce dopredu nevylučuje, ale pravdepodobnosť, že sa pomyselná gulička rulety zastaví na im priradenom výseku a dôjde tak k vybraniu jedného z nich, je menšia. Existuje niekoľko bežne používaných spôsobov, ako ruletové koleso skonštruovať. Líšia sa hlavne v spôsobe určovania veľkosti výsekov pre jednotlivé chromozómy. Veľmi rozšírený je takzvaný roletový mechanizmus výberu s pravdepodobnosťou výberu chromozómu priamo úmernou jeho ohodnoteniu (tzv. fitness-proportionate selection), kde má každý chromozóm priradený výsek, ktorého plocha je priamo úmerná ohodnoteniu tohto chromozómu. K vytvoreniu takéhoto ruletového kolesa stačí spočítať ohodnotenia všetkých členov populácie a potom priradiť každému chromozómu proporcionálne odpovedajúci kruhový výsek. Nech má uvažovaná populácia veľkosť a , nech je ohodnotenie i-teho chromozómu (predpokladáme, že ohodnocujúca funkcia je vždy nezáporná), potom pravdepodobnosť, s akou bude i-ty chromozóm vybraný, je daná nasledujúcim vzťahom: [3]