Použitie mikrouchopovačov MEMS
|
Trenčianska Univerzita Alexandra Dubčeka v Trenčíne
Fakulta Mechatroniky |
|
| Autor: | Juraj Prívara |
| Pedagogický vedúci: | Ing. Ján Zápotočný |
| Študijný odbor: | Mechatronika |
| Akademický rok |
2009/2010
|
| Abstrakt
Práca sa zaoberá mikro-pružnými mechanizmami so zameraním na uchopovanie mikro objektov. Prvá časť sa zameriava na teóriu mikrouchopovačov, problémy s nimi a popisom flexibilných mechanizmov, z ktorých sú štruktúry mikrouchopovačov odvodené. Ďalšia časť je zameraná na riešenie problémov a popisuje typy flexibilných kĺbov, ktoré poskytujú pohyb a správanie mikrouchopovačov. V tomto projekte hovoríme aj o materiáloch vhodných na použitie v tejto oblasti. |
| Abstract
This work deals with micro flexible mechanisms with a focus on griping of micro objects. The first part focuses on microgrippers theory, issues related to it and description of flexible mechanisms, from which are the structures of microgrippers derived. Next part is oriented on solving the issues and describes the types of flexible joints, which provide the movement and the behavior of microgrippers. In this project we also talk about the materials suitable for use in this area. |
Obsah
Úvod O mikrosystémoch a MEMS (Micro-Electro-Mechanical System) sa začalo hovoriť v 90. rokoch 20. storočia ako o nastupujúcej kľúčovej technike 21. storočí. Veľké úsilie bolo venované technickému vývoju a novým prístupom spojeným so systémovým inžinierstvom pre vývoj nových aplikácii. Mnohé z nich, ktoré boli skôr rozpracované iba v teoretické rovine, boli teraz uvedené do praxe a na ich základe začali vznikať nové, kvalitatívnejšie odlišné systémy. Jednou z hlavných predností mikrosystémovej techniky je možnosť mikrominiaturizácie, využitie materiálov používaných na výrobu integrovaných elektronických obvodov (napr. kremík), ktorý však práve v týchto aplikáciách vykazuje vlastnosti bežných materiálov: napr. kremík v mikroštruktúrach má vlastnosti ocele. Elektronicky riadené skalpely alebo biochemické laboratória vytvárané na čipe umožnili dosiahnuť veľkého pokroku v medicíne. Bez mikrosystémovej techniky by nebol možný rozvoj funkcii kardiostimulátorov, ktoré v dnešnej dobe predstavujú inteligentné systémy obsahujúce senzory, aktuátory, riadiacu elektroniku a inteligentný rozhodovací software. Veľké množstvo mikrosystémov je i v moderných automobiloch (airbagy, ABS, riadiace a monitorovacie systémy, navigačné systémy atď.). Bez mikrosystémových technológií by sa nerozvíjal kozmický výskum, letectvo, bezpečnostné systémy alebo ochrana životného prostredia. V mikrosystémoch sú často začlenené i celé nesúrodé súčasti. Vychádza sa z predpokladu, že v mikrosvete sa jednotlivé súčasti systému výrazne vzájomne ovplyvňujú, na rozdiel od makrosveta, kde vlastnosti jednotlivých súčastí sa dá považovať za oddelené, a pritom dohromady vytvárajú funkčný makrosystém. Pri manipulácii s veľmi malými súčiastkami sa vyvíjajú aj k nim patričné druhy manipulátorov, čiže inak povedané uchopovačov či mikrouchopovačov. Pri súčiastkach väčších ako sú milimetre sa využívajú uchopovače zostrojené z mechanických, guľových a krížových kĺbov. Pri mikrosúčiastkach, teda pri súčiastkach menších ako je milimeter sa musí zvoliť mikrouchopovač, ktorý však funguje na iných princípoch ako to je v makrosvete.
Základné problémy pri návrhu mikrouchopovača
Ako už bolo povedané exitujú rozdiely medzi makro a mikro svetom. Pri uchopovaní väčších súčiastok sa sily ako sú napríklad elektrostatická zanedbávajú, ale pri mikrosúčiastkach takéto sily vytvárajú veľký problém. Ďalším problémom pri návrhu je zvolenie správnych kĺbov. Keďže pri uchopovaní mikrosúčiastok mechanické kĺby treba vylúčiť z dôvodu ich nepresnosti, obtiažnej a nákladnej výrobe a vzniknutom trení pri ich pohybe. Pre potrebnú presnosť preto teda zvolíme kĺby z pružných materiálov tzv. flexibilné alebo pružné kĺby.
Paralelné a uhlové uchopenie telesa
Hlavný rozdiel medzi uchopením paralelným (obr.1.1) a uhlovým (obr.1.2) je ten že pri paralelnom nám pri uchopení telesa pôsobia sily len v smere osi x a pri uchytení uhlovom nám sily pôsobia pod uhlom, čiže sú zložené z x-ovej a y-ovej zložky. Samozrejme že existujú aj v týchto prípadoch parazitné sily. Pôsobenie síl však závisí aj od danej súčiastky. Napríklad ak manipulujeme so súmernou súčiastkou kruhového tvaru a jej paralelným uchopením tak nám pôsobia sily kolmo na súčiastku. Preto je paralelné uchopenie vhodne na kruhové súčiastky, pretože v nich nepôsobia sily v smere y, tým pádom je aj jednoduchší ich výpočet a lepšie držanie súčiastky v manipulátore. Pri uhlovom uchytení treba vyjadriť x-ové aj y-ové zložky sily. Nieje vhodné na uchytenie súmerných súčiastok, keďže môže dôjsť k ich vyšmyknutiu. Súbor:Paralelné uchopenie.jpg Súbor:Uhlové uchopenie.jpg
Sily pri uhlovom uchopení
Pri uchopovaní sa sily rozkladajú a pôsobia na teleso ako to je na obrázku (obr.1.3). FA a FB sú uchopovacie sily, ktoré pôsobia kolmo na teleso. Dotykové body A a B ležia na dotykovej čiare a na teleso tiež pôsobia trecie sily FtA a FtB. Trecia sila Ft je definovaná ako súčin koeficientu trenia μ a normálovej sily Fn, ktorá je kolmá na treciu silu Ft. V našom prípade funkciu normálovej sily preberá sila FA a FB, pričom platí, že trecia sila
FtA = μA.FA a FtB = μB.FB (1.1)
Koeficienty trenia μA a μB môžeme definovať ako
μA = tg ΦA a μB = tg ΦB (1.2)
kde uhly ΦA a ΦB predstavujú uhly trecieho kužeľa. Ich veľkosť závisí od polohy dotykových bodov, tvaru uchopovaného telesa tvaru ramien. Stláčacia čiara prechádza cez ťažisko a je kolmá na dotykovú čiaru. Z ťažiska kolmo na zem pôsobí tiažová sila G a zviera so stláčacou čiarou uhol φG. Na teleso ďalej pôsobí aj vonkajší točivý moment M v kladnom smere. Súbor:Rozloženie síl na teleso pri uhlovom uchopení.jpg
Statická rovnováha telesa pri uhlovom uchopení
Ak má byť teleso uchopované uhlovým uchopením v rovnováhe, výslednica síl, pôsobiacich na teleso vo všetkých smeroch, musí byť rovná nule, a teda musia platiť silové podmienky:
ΣFi x = 0 , (1.3)
kde ΣFix predstavuje sumu všetkých síl pôsobiacich na uchopované teleso v x-ovom smere podľa súradnicového systému vyznačeného na obrázku (Obr. 1.3). Podľa obrázku môžeme ďalej napísať,
FA x + FtA x − FB x − FBt x −Gx = 0 , (1.4) FAcosφA +FtAsinφA − FBcosφB − FtBsinφB − GsinφG =0 (1.5)
Dosadením výrazu (1.1) za FtA a FtB do vzťahu (1.5) získavame rovnicu reprezentujúcu silovú podmienku v x-ovom smere, pre spôsob uchopenia znázornený na obrázku (Obr. 1.3),
FAcosφA + μAFAsinφA − FBcosφB − μBFBsinφB − GsinφG =0 (1.6)
Dalšia silová podmienka predstavuje sumu všetkých síl, pôsobiacich na uchopované teleso v y-ovom smere, rovnú nule,
ΣFi y = 0 (1.7) FtA y + FtB y − FA y − FB y −Gy = 0, (1.8) FtAcosφA +FtBcosφB − FAsinφA − FBsinφB − GcosφG =0 (1.9)
Podobne ako pre silovú podmienku v x-ovom smere, dosadením výrazu (1.1) za FtA a FtB, získavame rovnicu silovej podmienky v y-ovom smere, μAFAcosφA + μBFBcosφB − FAsinφA − FBsinφB − GcosφG =0 (1.10) Ďalšou podmienkou je tzv. momentová podmienka, ktorá predstavuje sumu všetkých momentov k bodu O rovnú nule,
ΣMio = 0, (1.11) M + rA FA y − rA FtA y + rB FtB y − rBFB y − rt Gx = 0 (1.12) M+ r A FAsinφA − rAFtAcosφA + rBFtBcosφB − rBFBsinφB − rtGsinφG =0 (1.13) M+ r A FAsinφA − rAμAFAcosφA + rBμBFtBcosφB − rBFBsinφB − rtGsinφG =0 (1.14)
Po úprave výrazu (1.14) získavame rovnicu momentovej podmienky, pre spôsob uchopenia zobrazený na obrázku (Obr. 1.3),
M+ r A FA (sinφA − μAcosφA) + rBFB (μBcosφB − sinφB) − rtGsinφG =0 (1.15)
Čo je to MEMS alebo MST?
V Spojených štátoch je to technológia, známa ako Micro-Electro-Mechanical Systems (MEMS), v Európe je to len Microsystem Technologies (MST). Majú za úlohu presnejšie vymedzenie alebo vytváranie odpovedí, s niekoľkými spoločnými znakmi ako "miniaturizácia". MEMS je súčasť nástrojov, fyzických výrobkov, a metodík na spracovanie:
- Je to súbor techník a postupov pre navrhovanie a vytváranie miniatúrnych systémov
- Je to fyzický produkt často neštandartný a jedinečný ku konečnej aplikácii.
MEMS je aj spôsob, ako robiť veci. "Microsystems Technology" tento pojem presne definuje Úrad Spojených štátov pre pokročilý výskum obrany (DARPA- The Defense Advanced Research Projects Agency). Tieto "veci" zlučujú funkcie pre snímanie, ovládanie s výpočtami a komunikáciou s lokálnou kontrolou fyzikálnych parametrov na mikroúrovni. Hoci univerzálna definícia chýba, MEMS výrobky majú početné charakteristické rysy. Ide o miniatúrne systémy zahŕňajúce jednu alebo viac mikromechanických súčasti alebo štruktúr. Často menšie integrovateľné funkcie sa spájajú do jedného balíka pre väčšiu úžitkovosť. Môžu tiež priniesť výhody zníženia nákladov, priamo prostredníctvom nízkych jednotkových cien, alebo nepriamo znížením služby a nákladov na údržbu. Drvivá väčšina dnešných produktov MEMS sú v kategórií ako komponenty alebo podsystémy. Mikrosystémy sa stále ešte len vyvíjajú, ale ich vývoj napreduje. Ľudia sa spoliehajú na úspech dnešných komponentov najmä preto, že tieto komponenty sú schopné vykonať funkciu v stále rastúcej zložitosti. Mikrosystém je vo fázy evolúčného procesu. Posledných tridsať rokov sme strávili učením sa, ako zostaviť mikromechanické komponenty. Len nedávno sme sa začali učiť o ich bezproblémovej integrácie do subsystémov, a nakoniec do kompletných mikrosystémov.
Pružné Mechanizmy
Pružné mechanizmy vykonávajú zmenu polohy vychyľovaním flexibilných (pružných) členov, namiesto pohyblivých kĺbov pri tuhých mechanizmoch.
História pružných mechanizmov
Podstata pružných členov na uchovanie energie a vytváranie pohybu bol použitý pred tisícročiami. Archeologické dôkazy ukazujú, že luky požívané od roku 8000 pred n.l. boli primárnou zbraňou na lov vo väčšine kultúr.
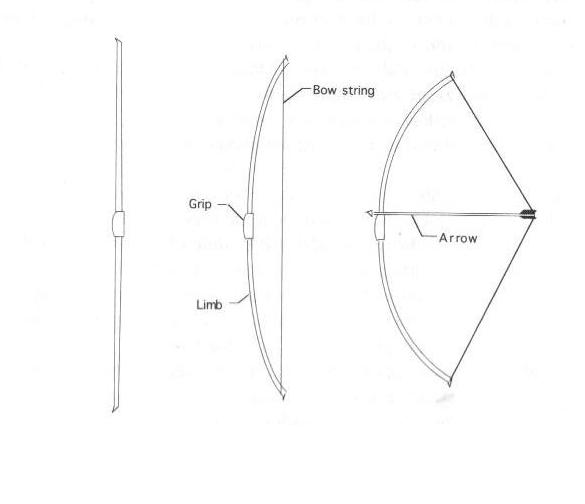Včasné luky boli vyrobené z relatívne pružných materiálov ako je drevo a zvieracie šľachy. Deformačná energia na prove sa premieňa na kinetickú energiu šípu.
Praky sú ďalším príkladom včasného uplatňovania pružných členov. Používali ich Gréci už vo štvrtom storočí pred n.l.
Včasné katapulty boli postavené z drevených častí, ktoré boli odklonené na uchovanie energie a po uvoľnení vymrštili daný predmet.
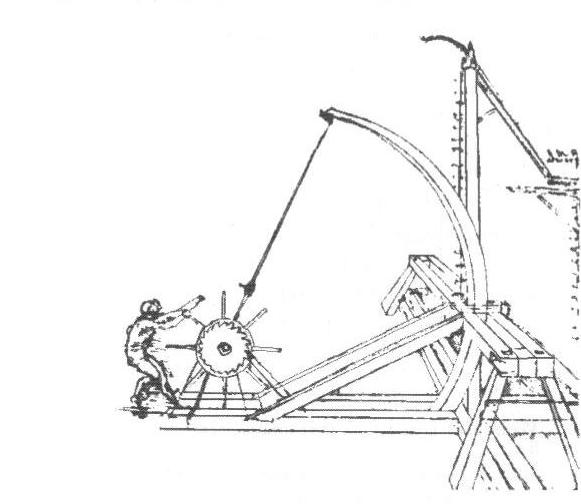
Iné metódy boli vyvinuté na začiatku dvadsiateho storočia. Našlo sa nové využitie pre tento druh pohybu. Počet produktov, ktoré využívajú pružnosť materiálov na výkon svojich funkcií výrazne vzrástol v niekoľkých posledných desaťročiach čiastočne vďaka objaveniu a výrobe silnejších a spoľahlivejších materiálov. Využitie pružnosti materiálov sa bude pravdepodobne aj naďalej zvyšovať s časom a konštrukčné materiály a metodiky sa budú zlepšovať. V dnešnej dobe je obrovský dopyt, zvyšuje sa kvalita výrobkov a znižujú náklady. Univerzity a priemyselný výskum zohrávajú dôležitú úlohu vo vývoji mechanizmov s využitím pružných materiálov.
Konštrukcia pružných mechanizmov
Výroba mikro a miniatúrnych mechanizmov je veľmi náročná. Nedajú sa vyrobiť bežnými výrobnými postupmi. Jediná možnosť ako ich zhotoviť je zvoliť vhodnú metódu na tvorbu mikroštrukúr ako sú napríklad laserové alebo iónové mikroobrábanie, galvanické pokovovanie, kremíková technológia. Hlavnou výhodou pružných mechanizmov je zníženie nákladov z dôvodu redukovania konštrukčných dielov a najmä zjednodušenie výrobného procesu. Ďalšie výhody sú presnosť, spoľahlivosť a minimálna údržba. Ako už bolo spomenuté tieto zariadenia sú vyrobených z jedného kusa materiálu. Obsahujú menej pohyblivých častí, ako sú napríklad čapy alebo rôzne klzné časti, ktoré je nutné mazať. Majú minimálny počet spojov, čím sa zvyšuje presnosť mechanizmu. Je to najmä vďaka pružným prvkom, ktoré dokážu zabezpečiť bezvôľový pohyb jednotlivých častí mechanizmu. Pohyb v pružných mechanizmoch je zabezpečený vychyľovaním jednotlivých prvkov, tým pádom sú nehlučné a nevzniká žiadna vybrácia.
Pružné kĺby
Pružný kĺb je prvok v rámci konštrukcie, ktorý vďaka svojej pružnosti umožňuje pohyb medzi dvoma susediacimi nehybnými časťami.
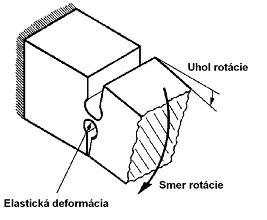Pružný kĺb môžeme zabezpečiť pomocou pružného elementu ako je napríklad tenký oceľový pásik uchytený medzi pevné nepohybujúce sa časti.
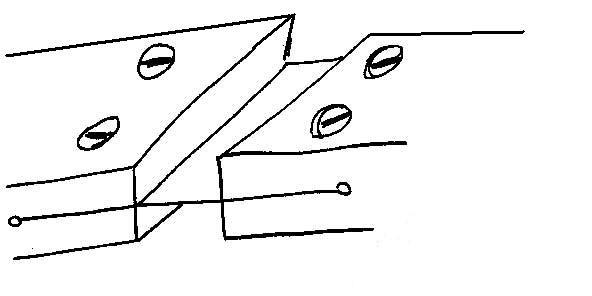Pružný kĺb môžeme dosiahnuť aj opracovaním materiálu tak, aby v mieste ohybu vznikol vrub, teda vytvorí sa ohybové tenké spojítko. V tomto prípade predchádzame rozdeleniu materiálu.
Výhody pružných kĺbov
Berme do úvahy len monolitické pružné kĺby. Keďže sú vyrobené z jedného kusa materiálu majú oproti mechanickým značné výhody:
- Žiadne straty spôsobené trením
- Nie je potrebné mazanie
- Nie sú citlivé na znečistenie
- Uloženie je bez vôle
- Žiadna hysterézia
- Kompaktnosť
- Jednoduché zhotovenie
- Prakticky žiadna potrebná údržba
Nevýhody pružných kĺbov
Nevýhody sa týkajú najmä obmedzení:
- Kĺby sú schopné poskytnúť pomerne nízku úroveň rotácii.
- Rotácie nie je čistá, pretože vzniká axiálne strihanie prípadne aj torzia zaťaženia, okrem ohýbania.
- Ohýbanie kĺbu je zvyčajne citlivé voči zmenám teploty.
Jeho rozmery sa menia v dôsledku tepelnej rozťažnosti čo vedie k zmenám oproti pôvodným hodnotám. Mechanizmus s kĺbmi bude fungovať, kým sa niečo nepokazí. Zvyčajne to býva samotný kĺb v dôsledku únavy alebo preťaženia materiálu.
Materiál pre mikrouchopovače
Mnoho rôznych typov materiálov môže byť použité pre dizajn pružného mechanizmu. I keď každá aplikácia má svoje vlastné kritériá pre výber materiálov, môže sa proces výberu riadiť princípmi, ktoré možno použiť v mnohých situáciách. Snáď najdôležitejšie na zapamätanie je, že tuhosť a sila nie sú rovnaké a je možné, aby materiál bol pružný a silný. Tvárnosť a pružnosť tiež nie sú rovnocenné. Krehké materiály môžu byť použité na výstavbu kompatibilných mechanizmov, ak je ich geometria prispôsobená tak, že nie sú preťažené. Ďalším dôležitým bodom je to, že mechanizmus môže byť flexibilný buď vďaka geometrii, alebo vlastnosťou materiálu. V konečných návrhoch sa uprednostňuje čo najväčšia flexibilita pred tuhosťou.
Medza klzu a Youngov modul pružnosti
Youngov modul E je pre väčšinu kovov takmer rovnaký bez ohľadu na pridaní legujúcich prvkoch alebo tepelného spracovania. Medzu klzu σK a pevnosť v ťahu môžeme zvýšiť pomocou tepelného spracovania alebo tvarovania za studena. Nevýhodou toho je že sa tým tiež tieto materiály stávajú krehkejšími a zvyšuje sa riziko výskytu chýb, prasklín, nečistôt a tiež sú citlivejšie na zvýšené napätie. Materiály s vysokou pomernou hodnotou pevnosti a modulu pružnosti dovoľujú väčšie priehyby pred tým ako sa v nich vyskytne chyba. Tento pomer je jedným z najdôležitejších parametrov pri výbere materiálu pre pružné mechanizmy.
Materiály pre pružné mechanizmy
Kovy
Kovy, ako je oceľ, by mal byť z nerezovej ocele, hliníka, titánu atď. Pri návrhu treba brať do úvahy:
- Predpokladané správanie materiálov (vo vysoko presných prístrojoch)
- Dobrý výkon v prostrediach s vysokou teplotou
- Biokompatibilita
- Nízka náchylnosť na sklz
- Predvídateľná únavová životnosť
- Schopnosť pracovať v mnohých nepriaznivých podmienkach
- Elektrická vodivosť (ako je potrebné pre flexibilné elektrické konektory)
Niektoré nevýhody kovov v súlade s mechanizmami zahŕňajú:
- Náklady na materiál
- Náklady na tvárnenie a obrábanie materiálov
- Väčšia potreba spojovacích komponentov
- Vysoká hustota
- Nízky pomer medze klzu k Youngovmu modulu v porovnaní s mnohými polymérmi
Plasty
Hoci cena niektorých plastov je porovnateľná s oceľou, ale náklady na ich spracovanie klasickými metódami je výrazne nižšia ako u iných materiálov vo veľkých objemoch. Toto a ich vysoká pomerná hodnota pevnosti a modulu pružnosti sú hlavné dôvody pre ich použitie pri vysokej presných mechanizmoch. Výhody plastov zahŕňajú:
- Nízke výrobné náklady vo veľkých objemoch
- Vsoká pomerná hodnota pevnosti a modulu pružnosti
- Obrobiteľnosť
- Žiadne spojovacie súčiastky
- Nízka hustota
- Biokompatibilita
- Elektricky izolačné vlastnosti
Nevýhody plastov:
- Variabilita mechanických vlastností plastov ich robí menej predvídateľné ako u iných materiálov
- Nízke teploty topenia materiálu a degradácia v niektorých prostrediach
- Zhoršenie vlastnosti v niektorých prostrediach
Sklo je často používané na posilnenie plastov. Toto posilnenie zvyšuje pevnosť aj tuhosť, čo má za následok zníženie pomernej hodnoty pevnosti a modulu pružnosti. Polypropylén je bežne používaný polymér z niekoľkých dôvodov. Po prvé, je to jeho vysoký pomer medze sklzu k Youngovmu modulu, ako je uvedené v tabuľke 5.1. Má tiež rad výhod v porovnaní s inými polyméry. Polypropylén je ľahko dostupný, lacný, ľahko spracovateľný a má nízku hustotu. Je tiež veľmi tvárny. Hoci to je vynikajúci materiál pre mnohé kompatibilné mechanizmy, nie je vhodný v niektorých prípadoch. A to z dôvodu tečenia, ma obmedzený teplotný rozsah a malú chemickou odolnosť.
Ostatné materiály
Diely z krehkých materiálov môžu byť tiež použite v pružných mechanizmoch, ale sú citlivé na prepätie. Keď sú krehké materiály používané ako vyhovujúci materiál, je to zvyčajne preto, že dizajn je obmedzený ďalšími faktormi. To je prípad, kedy sú mechanizmy konštruované s pomocou technológií na výrobu integrovaných obvodov. Materiály sú obmedzené na tie, ktoré sú vhodné pre techniky, z ktorých väčšina je veľmi krehká. Optické časti sú ďalším príkladom toho. Flexibilná časť je vyrobená z krehkého materiálu, pretože podstatné obmedzenie je spojené s aplikáciou. Kompozitné materiály (napr. grafit, sklenené vlákno, a sklolamináty), elastoméry, textílie a iné materiály sú považované za vyhovujúce pre použitie v mechanizmoch ak daná aplikácia vyžaduje ich použitie. Je dôležité zvážiť všetky požiadavky pri výbere materiálu, pretože veľa vecí, ktoré sa tradične používajú v tuhých štruktúrach môžu byť upravené tak aby boli požité v pružných mechanizmoch.
Riešenie pružných mechanizmov pomocou metódy konečných prvkov
Keďže pružné mechanizmy sú zhotovené z materiálov ktoré podstupujú veľké pružné deformácie pri malej zmene objemu, je veľmi ťažké ich výpočet. Nedajú sa vypočítať ako staticky lineárne úlohy, z dôvodu že ich deformácia je plne elastická. Aby sme získali obraz o závislosti napätia a pomernej deformácii je potrebné vykonať ťahovú skúšku a jej výsledky použijeme ako vstupné parametre pre metódu konečných prvkov. Táto metóda je použiteľná za pomoci počítača. Je to spôsob výpočtu pomocou matematického modelu, ktorý sa vytvorí na základe vymodelovaného tvaru súčiastky a zadaní okrajových podmienok. Pri konštruovaní súčiastok namáhaných či už tepelne alebo mechanicky je veľmi vhodnou a v poslednej dobe aj čoraz častejšie využívanou podpornou metódou tzv. FEM (Finite Element Method) modelovanie. Použitím metódy konečných prvkov a pomocou programov (napr. ANSYS, ABAQUS) je možné simulovať zaťaženie súčiastky a vypočítať tak pôsobenie zaťaženia v objeme. Jedná sa najmä o distribúciu napätí a nájdenie najkritickejších miest s vysokou lokálnou hodnotou napätia.
Postup pri simulácii v programe
V prvom rade je potrebné programu dodať samotný model súčiastky, ktorý sa dá narysovať priamo v danom FEM programe alebo v ktoromkoľvek kresliacom konštruktérskom programe s jeho následným importovaním do FEM programu. Ak už je model súčiastky vytvorený, musíme programu zadať materiálové vlastnosti. Pre jednoduché výpočty statického zaťažovania (väčšina súčiastok v strojárstve) programu pre správne fungovanie väčšinou postačujú hodnoty veľkosti modulu pružnosti, poissonovho čísla (predstavuje absolútnu hodnotu podielu pomerných deformácií), prípadne hustoty. Veľký dôraz je potrebné klásť na jednotky zadávaných veličín! Väčšinou je vhodné zadávať ich v jednotkách SI sústavy. Po zadaní materiálových vlastností nasleduje navrhnutie a vytvorenie tzv. siete (mesh). Súčiastka sa rozdelí na množstvo malých elementov, napríklad na hexagonály tehličkového tvaru (brick elements), pričom každý z elementov má vo svojich uzlových bodoch (nodes) definované materiálové vlastnosti, ktoré sme programu zadali v predchádzajúcom kroku. Vytvorenie siete je najdôležitejším krokom pred samotným výpočtom, pretože pri generácii zle navrhnutej siete môže dochádzať k deformovaniu elementov v oblastiach so zložitým tvarom súčiastky – to následne pri výpočte zapríčiní, že program nedokáže výpočet dokončiť. Tvarovo zložité oblasti je preto vhodné opatriť jemnejšou sieťou, avšak pozor – čím jemnejšia sieť, tým dlhší je proces výpočtu. Nasleduje zaťaženie súčiastky, ktorú je potrebné najprv „ukotviť“, teda určiť pre niektoré z bodov alebo plôch súčiastky počet stupňov voľnosti. Potom môžeme aplikovať vonkajšie napätie. Ak máme za sebou aj fázu zaťažovania, môžeme sa pokúsiť o prevedenie výpočtu. Dôležitým krokom býva nastavenie dĺžky časového kroku výpočtu, resp. počtu krokov, pretože počas výpočtu musí dochádzať ku tzv. iterácii. Metódy iterácie sú užitočné pri riešení (spravidla) veľkých sústav lineárnych rovníc postupným približovaním sa k presnému riešeniu. V prvom rade je dôležité uvedomiť si, že samotné bezproblémové prebehnutie výpočtu neznamená, že jeho výsledky budú v poriadku. Je nevyhnutnosťou v prvom rade posúdiť na základe platných fyzikálnych zákonov a pravidiel, či výsledok spĺňa podmienky logiky.
