Návrh mikrouchopovača
Obsah
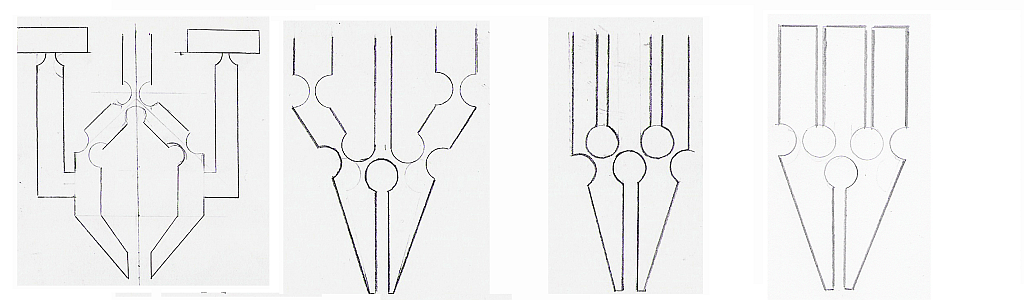
Na obrázkoch 6.1 sú znázornené náčrtky postupného vyvíjania a zjednodušovania mikrouchopovača s dosiahnutým výsledkom, a ten je najjednoduchšia a najúčinnejšia konštrukcia mikromanipulátora.
Základné vlastnosti mikrouchopovača
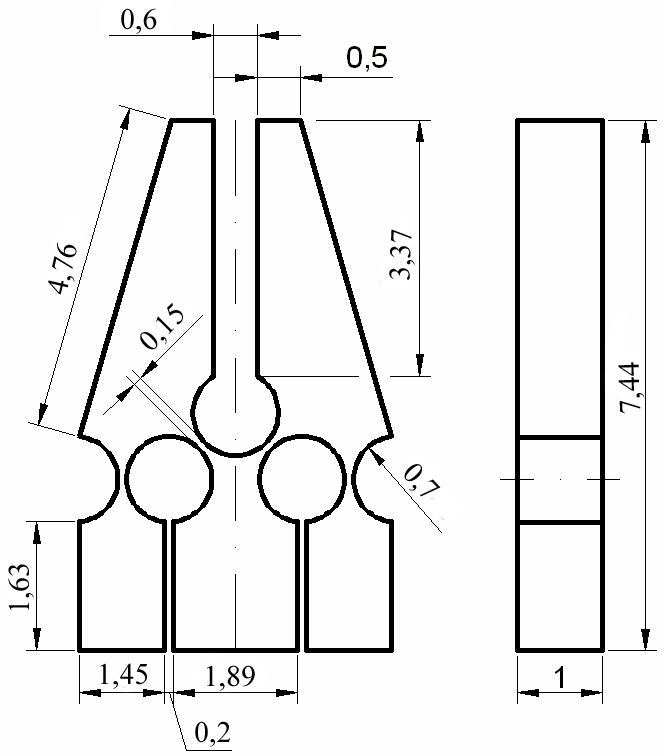
Ako najvhodnejšie kĺby pre daný mikrouchopovač sa javia kĺby s kruhovým zárezom, ktoré zabezpečia žiadaný ohyb. Z tabuľky materiálov som zvolil ako najvhodnejší materiál Nylon (type 66), ktorý ma veľmi dobré vlastnosti čo sa týka ohybov a je málo náchylný na plastické poruchy. Základné kritéria ktoré si môžeme určiť a od nich sa budú odvodzovať ostatné sú:
- veľkosť menšia ako 10mm na výšku, keďže sa jedná o mikrosúčiastku
- hrúbka 1mm
- maximálne otvorenie čeľustí 0,6mm
- pohyb čeľuste po úplnom uzatvorení 0,3mm
- uchopovacia sila 10mN
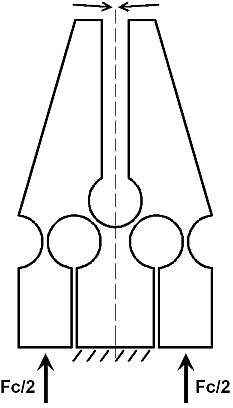
- mikrouchopovač bude využívať uhlové uchopenie telesa, čo je zrejmé z náčrtu
Na bočné časti mikrouchopovača bude pôsobiť vstupná sila, budú vykonávať nepatrný pohyb. Stredná časť ostane nehybná, teda bude ukotvená.
Pohybová analýza mikrouchopovača
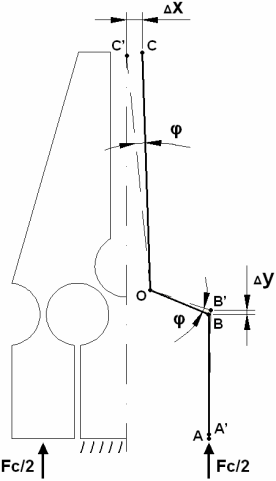
Ako prvé je potrebné vypočítať veľkosť posunutia Δy, ktoré je potrebné na uzatvorenie a otváranie čeľusti. Mikrouchopovač je symetrický podľa osi, preto nám na výpočet stačí vychádzať len z jednej polovice. Ako veľkosť posunutia čeľuste v x-ovom (Δx) smere sme si zvolili 0,3mm. Zvolené rozmery:
- posunutie v x-ovom smere Δx: 0,3mm
- spojnica medzi kĺbmi O a B: 1,4mm
- spojnica medzi kĺbmi O a C: 4,36mm
Výpočty Δy a uhla φ
Celý pohyb mikrouchopovača spočíva v jednom ohybovom mieste O. Potom veľkosť uhla φ (uhol medzi OB a OB‘) je rovnaká ako veľkosť uhla medzi OC a OC‘. Môžeme teda napísať vzťah [math]\sin \phi =\frac{\Delta y}{OB}[/math] a [math]\sin \phi =\frac{\Delta x}{OC}[/math] z ktorých vyplýva
|
[math]\frac{\Delta y}{OB}=\frac{\Delta x}{OC}[/math] |
(6.1) |
Tento vzťah ak upravíme a dosadíme konkrétne zvolené hodnoty, dostaneme vzťah výpočtu pre posunutie Δy,
|
[math]\Delta y=\frac{\Delta x}{OC}.OB=\frac{0,3}{4,36}.1,4=0,0963\left[ mm \right][/math] |
(6.2) |
V ďalších výpočtoch budeme potrebovať veľkosť uhla φ v radiánoch, čiže
|
[math]\phi =\arcsin \frac{\Delta x}{OC}=\arcsin \frac{0,3}{4,36}=3,945\left[ {}^\circ \right]=3{}^\circ 56[/math] |
(6.3) |
|
[math]\phi \left[ rad \right]=\frac{\phi }{180}.\pi =\frac{3,945}{180}.\pi =0,0688\left[ rad \right][/math] |
(6.4) |
Výpočet údajov pre pružné kĺby
Ako najvhodnejší materiál pre pružné kĺby bol vybraný nylon s hodnotou modulu pružnosti E=2,8 GPa. Rozmery pre pružné kĺby sú
- šírka kĺbu (hrúbka) w=1,4 mm
- hrúbka zúženej časti t=0,15 mm
- polomer kruhového zárezu kĺu r=0,7 mm
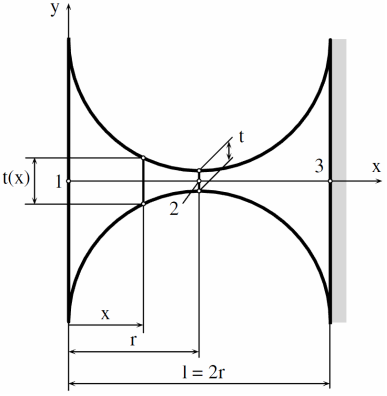
premenlivá hrúbka pružného kĺbu sa dá vypočítať podľa literatúry [3]:
|
[math]t(x)=t+2\left[ r-\sqrt{x(2r-x)} \right][/math] |
(6.5) |
Výpočet poddajnosti a tuhosti kĺbu v smere rotácie
V literatúre je vzťah pre výpočet poddajnosti pružného kĺbu s kruhovým zárezom v smere rotácie ψ [3] ako
{{Vzorec|[math]{{C}_{\Psi }}=\frac{12}{E.w}.I[/math]|6.6}
kde I predstavuje integráciu premenlivej hrúbky kĺbu, [math]I=\int\limits_{0}^{I}{\frac{dx}{t{{(x)}^{3}}}}[/math] a po dosadení do vzťahu pre výpočet poddajnosti pružného kĺbu dostaneme vzťah
|
[math]{{C}_{\Psi }}=\frac{12}{E.w}.\int\limits_{0}^{I}{\frac{dx}{t{{(x)}^{3}}}}[/math] |
(6.7) |
Po dosadení vzťahu t(x) do vzťahu (6.7) a po jeho integrácii získavame vzťah pre výpočet poddajnosti pružného kĺbu v smere rotácie ψ:
|
[math]{{C}_{\psi }}=\frac{24.r}{E.w.{{t}^{3}}.(2r+t).{{(4r+t)}^{3}}}.\left[ t(4r+t).(6{{r}^{2}}+4rt+{{t}^{2}})+6r{{(2r+t)}^{2}}\sqrt{t(4r+t)}.\arctan \sqrt{1+\frac{4r}{t}} \right][/math] |
(6.8) |
Po dosadení hodnôt modulu pružnosti a rozmerov kĺbu dostávame hodnotu poddajnosti pružného kĺbu Cψ=2550 mN-1
V ďalších výpočtoch budeme potrebovať hodnotu pre tuhosť kĺbu v smere rotácie ψ. Tú dostaneme tak, že je prevrátenou hodnotou poddajnosti, čiže
|
[math]{{K}_{\psi }}=\frac{1}{{{C}_{\psi }}}=\text{3},\text{92}.\text{1}{{0}^{-\text{4}}}\text{N}{{\text{m}}^{-\text{1}}}[/math] |
(6.9) |
Výpočet celkovej vstupnej sily
Celková vstupná sila je sila, ktorú musíme dodať mechanizmu aby sme ho uviedli do činnosti. Skladá sa z dvoch síl, a to deformačnej (Fd) a pracovnej (Fp). Deformačná sila spôsobuje pružné deformácie v kĺboch a pracovná umožňuje aby mechanizmus konkrétny predmet uchopil.
|
[math]{{\text{F}}_{\text{c}}}=\text{ }{{\text{F}}_{\text{d}}}+{{\text{F}}_{\text{p}}}[/math] |
(6.10) |
Výpočet deformačnej sily
Keďže potenciálna energia pružnosti mechanizmu je rovná súčtu potenciálnych energii pružnosti jednotlivých kĺbov, potom
|
[math]\frac{1}{2}{{K}_{c}}.\Delta {{y}^{2}}=\sum\limits_{i=1}^{4}{\frac{1}{2}{{K}_{i}}.\phi _{i}^{2}}[/math] |
(6.11) |
kde Kc je tuhosť celého mechanizmu, Δy je posunutie v y-ovom smere, Ki predstavuje tuhosť jednotlivých kĺbov a φ je pootočenie kĺbov. Vyjadrením zo vzťahu (6.11) získame výpočet celkovej tuhosti mechanizmu:
|
[math]{{K}_{c}}=\frac{4.K.{{\phi }^{2}}}{\Delta {{y}^{2}}}=800,3323N{{m}^{-1}}[/math] |
(6.12) |
Ďalej môžeme zistiť deformačnú silu Fd ak vynásobime Kc a Δy:
|
[math]{{F}_{d}}={{K}_{c}}.\Delta y=\text{8}00,\text{3323}\cdot 0,0\text{963}.\text{1}{{0}^{-\text{3}}}=0,0\text{77}0\text{7}[/math] |
(6.13) |
Výpočet pracovnej sily
Na výpočet pracovnej sily treba brať do úvahy zosilnenie síl (G), ktoré môžeme vyjadriť ako pomer posunuti v x-ovom a y-ovom smere, vychádzame zo vzťahu pre výpočet deformačnej sily (6.1), ktorý keď upravíme dostávame
|
[math]G=\frac{\Delta x}{\Delta y}=\frac{OC}{OB}=\frac{4,36}{1,4}=3,11[/math] |
(6.14) |
Ako sme na začiatku uviedli, uchopovaciu silu sme si zvolili Fu=10mN=0,01N. Pracovná sila sa dá vyjadriť vzťahom
|
[math]{{F}_{p}}=\frac{{{F}_{u}}}{G}=\frac{0,01}{3,11}={{3,2154.10}^{-3}}N[/math] |
(6.15) |
Celková vstupná sila sa bude rovnať súčtu deformačnej sily Fd a pracovnej sily Fp,
|
[math]{{F}_{c}}={{F}_{d}}+{{F}_{p}}=0,07707+{{3,2154.10}^{-3}}=0,0803N=80,3mN[/math] |
(6.16) |
Kontrola ohybového napätia v kĺbe
Podľa literatúry je vzťah pre ohybové napätie pružného kĺbu s vrubovým zárezom (4.4),
|
[math]\frac{{{\sigma }_{\psi }}}{E.\phi }=-0,0028+0,6397\sqrt{\frac{t}{2r}}-0,0856{{\left( \sqrt{\frac{t}{2r}} \right)}^{2}}[/math] |
(6.17) |
kde E je modul pružnosti materiálu kĺbu, φ je uhol maximálneho ohybu, t je hrúbka zúženej časti kĺbu a r je polomer kruhového vrubu na kĺbe. Zo vzťahu (6.17) dostávame vzťah pre výpočet ohybového napätia
|
[math]{{\sigma }_{\psi }}=E.\phi .\left[ -0,0028+0,6397\sqrt{\frac{t}{2r}}-0,0856{{\left( \sqrt{\frac{t}{2r}} \right)}^{2}} \right][/math] |
(6.18) |
Dosadením hodnôt dostávame hodnotu maximálneho ohybového napätia v pružnom kĺbe: σP=38,02 MPa.
Veľkosť napätia na hranici pružnosti pre Nylón je σP=55 MPa. Splnili sme teda podmienku σψ≤σP, z toho vyplýva že zvolený materiál a rozmery uchopovača vyhovujú.