Teória grafov
Obsah
Teória grafov
V matematike a počítačových vedách sa teória grafov zaoberá štúdiom grafov, teda grafických matematických štruktúr používaných na modelovanie vzájomných vzťahov medzi objektami z určitej množiny. Teória grafov je súčasťou diskrétnej matematiky.
Základné pojmy a charakteristika grafov
V matematike sa pojem graf používa najčastejšie v zmysle grafického znázornenia určitej funkcie , napr. y=f(2x+3). Grafy, ktoré sú objektom štúdia teórie grafov sú však svojou povahou veľmi vzdialené od grafov funkcií. Sú to objekty tvorené určitou množinou bodov a čiar, ktoré tieto body spájajú na základe určitých pravidiel. Graf môžu tvoriť napr. mestá pospájané železnicou, rôzne miesta prepojené mostami ale aj elektrické siete alebo chemické zlúčeniny.
K tomu, aby bol zadaný graf (označíme ho φ) je treba, aby boli dané dve množiny: množina vrcholov V (predtým zmieňované body v grafe) a množina hrán H (zmienené čiary). Vo väčšine prípadov sú obe množiny konečné, avšak nie je to nutná podmienka existencie grafu. Graf potom zapisujeme ako φ=VH, prípadne φ=(V,H).
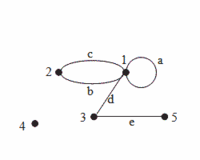
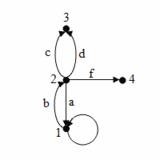
Ku každej hrane musia patriť dva vrcholy, ktoré sú touto hranou spojené a nazývajú sa krajné vrcholy hrany. Hovoríme aj, že krajné vrcholy ležia na spoločnej hrane. Vrcholy sa nazývajú susednými ak existuje taká hrana, na ktorej oba vrcholy ležia. Môže však existovať aj vrchol, ktorý nepatrí k žiadnej hrane. V takomto prípade hovoríme o izolovanom vrchole. K tomu, aby z množín vrcholov a uzlov mohol vzniknúť graf je ďalej potrebné poznať pravidlo, na základe ktorého vieme určiť, ktoré dvojice vrcholov majú byť spojené hranou. Jednotlivé hrany môžu tiež určovať smer vzájomnej interakcie krajných vrcholov. Vtedy hovoríme o orientovanej hrane a označujeme ju šípkou. Graf, ktorý obsahuje len orientované hrany sa nazýva orientovaný graf. Ak sú v grafe orientované aj neorientované hrany, ide o zmiešaný graf. Krajné vrcholy pri orientovaných hranách sú potom nazvané počiatočný a koncový vrchol hrany. Slučku v grafe tvorí hrana, ktorej krajné vrcholy splývajú (sú tvorené jedným vrcholom). Priľahlé hrany sú také, ktoré majú aspoň jeden spoločný krajný vrchol. Dve navzájom rôzne hrany, ktoré majú rovnaké krajné vrcholy sa v neorientovanom grafe nazývajú rovnobežné. V orientovanom grafe potom takéto hrany rozlišujeme podľa orientácie na súhlasne rovnobežné a nesúhlasne rovnobežné. Neorientovaný graf je jednoduchý ak v ňom neexistujú žiadne rovnobežné hrany [26].
Základné druhy grafových štruktúr
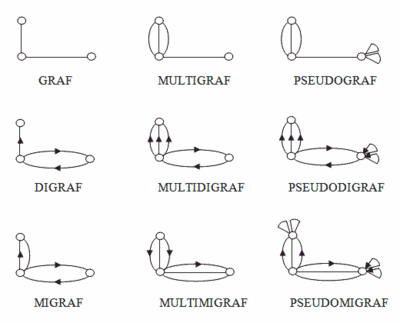
Najvšeobecnejšiu grafovú štruktúru predstavuje pseudomigraf. Od tohto typu grafu sa potom postupnými obmedzeniami dajú získať všetky podskupiny. Dôležitú úlohu pri určovaní typu grafovej štruktúry hrá násobná hrana. Rovnobežné hrany sa nazývajú násobné ak sú všetky neorientované alebo ak sú všetky orientované a majú rovnakú orientáciu. Rôzne druhy grafov sú znázornené na obr. 5. Počet hrán, ktoré vychádzajú z jedného vrcholu sa označuje aj ako stupeň vrcholu.
Graf neobsahuje orientované hrany, slučky ani násobné hrany. Takýto graf sa nazýva aj jednoduchý graf. Multigraf neobsahuje orientované hrany a slučky. Pseudograf neobsahuje orientované hrany.
Digraf (z angl. digraph = directed graph, v prekl. orientovaný graf) neobsahuje neorientované hrany, slučky a násobné hrany (rôzne orientované rovnobežné hrany obsahovať môže). Multidigraf neobsahuje neorientované hrany a slučky. Pseudodigraf neobsahuje len neorientované hrany.
Migraf (z angl. mixed graph, v prekl. zmiešaný graf) neobsahuje násobné hrany a slučky. Multimigraf neobsahuje slučky. Pseudomigraf môže obsahovať všetky druhy hrán [27].
Každý z týchto typov grafových štruktúr môže mať k prvkom svojej štruktúry priradenú určitú hodnotu (váhu), ktorá reprezentuje výhodnosť prechodu daným prvkom. Takýto graf potom nazývame ohodnotený alebo vážený graf. Rozoznávame hranovo ohodnotený graf a vrcholovo ohodnotený graf. Ohodnotené hrany môžu napr. reprezentovať vzdialenosti medzi miestami, ktoré predstavujú jednotlivé vrcholy. Ohodnotené môžu byť hrany aj vrcholy zároveň a to aj viacerými hodnotami, kde každá hodnota predstavuje inú veličinu (napr. vzdialenosť, čas, cenu, atď). Pomocou takto ohodnotených grafov sa dá reprezentovať a riešiť množstvo praktických problémov, z ktorých najvýznamnejšie sú rozpísané v nasledujúcej kapitole.
Typy problémov riešených pomocou teórie grafov
Štúdiom a hľadaním riešení problémov reprezentovaných rôznymi typmi grafov sa zaoberá [[#Teória grafov
| teória grafov]]. História teórie grafov je hlavne oproti iným oblastiam matematiky pomerne krátka. Prvé zmienky o úlohách vyjadrených grafmi súviseli s rôznymi hlavolamami a za skutočný počiatok teórie grafov sa považuje až riešenie hlavolamu známeho pod názvom Problém Kaliningradských mostov (vtedajší Königsberg, v preklade Kráľovec), ktoré publikoval významný matematik Leonhard Euler v roku 1736. Prvú knihu o teórii grafov však napísal až v roku 1936 Dénes König. Odvtedy sa toto odvetvie matematiky výrazne rozvíja a nachádza uplatnenie v rôznych oblastiach ľudskej činnosti.