Teória grafov

Obsah práce

1.	Teória hier
2.	Teória grafov
3.	Aplikácia stromov a princípov z teórie hier v niektorých ťahových hrách
4.	Implementácia algoritmov z teórie hier a teórie grafov do spoločenskej hry dáma

Teória grafov

V matematike a počítačových vedách sa teória grafov zaoberá štúdiom grafov, teda grafických matematických štruktúr používaných na modelovanie vzájomných vzťahov medzi objektami z určitej množiny. Teória grafov je súčasťou diskrétnej matematiky.

Základné pojmy a charakteristika grafov

Obr. 3 – Príklad neorientovaného grafu a je slučka, b a c sú rovnobežné hrany, 4 je izolovaný vrchol, d a e sú susedné (priľahlé) hrany; uzol 1 leží na hranách a, b, c, hrana c spája uzly 1 a 2.

Obr. 4 – Príklad orientovaného grafu E je slučka, a a b sú nesúhlasne rovnobežné hrany, c a d sú súhlasne rovnobežné hrany. 2 je počiatočný a 4 koncový uzol hrany f.

V matematike sa pojem graf používa najčastejšie v zmysle grafického znázornenia určitej funkcie , napr. y=f(2x+3). Grafy, ktoré sú objektom štúdia teórie grafov sú však svojou povahou veľmi vzdialené od grafov funkcií. Sú to objekty tvorené určitou množinou bodov a čiar, ktoré tieto body spájajú na základe určitých pravidiel. Graf môžu tvoriť napr. mestá pospájané železnicou, rôzne miesta prepojené mostami ale aj elektrické siete alebo chemické zlúčeniny.

K tomu, aby bol zadaný graf (označíme ho φ) je treba, aby boli dané dve množiny: množina vrcholov V (predtým zmieňované body v grafe) a množina hrán H (zmienené čiary). Vo väčšine prípadov sú obe množiny konečné, avšak nie je to nutná podmienka existencie grafu. Graf potom zapisujeme ako φ=VH, prípadne φ=(V,H).

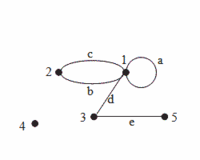
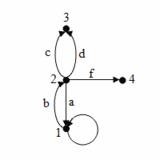
Ku každej hrane musia patriť dva vrcholy, ktoré sú touto hranou spojené a nazývajú sa krajné vrcholy hrany. Hovoríme aj, že krajné vrcholy ležia na spoločnej hrane. Vrcholy sa nazývajú susednými ak existuje taká hrana, na ktorej oba vrcholy ležia. Môže však existovať aj vrchol, ktorý nepatrí k žiadnej hrane. V takomto prípade hovoríme o izolovanom vrchole. K tomu, aby z množín vrcholov a uzlov mohol vzniknúť graf je ďalej potrebné poznať pravidlo, na základe ktorého vieme určiť, ktoré dvojice vrcholov majú byť spojené hranou. Jednotlivé hrany môžu tiež určovať smer vzájomnej interakcie krajných vrcholov. Vtedy hovoríme o orientovanej hrane a označujeme ju šípkou. Graf, ktorý obsahuje len orientované hrany sa nazýva orientovaný graf. Ak sú v grafe orientované aj neorientované hrany, ide o zmiešaný graf. Krajné vrcholy pri orientovaných hranách sú potom nazvané počiatočný a koncový vrchol hrany. Slučku v grafe tvorí hrana, ktorej krajné vrcholy splývajú (sú tvorené jedným vrcholom). Priľahlé hrany sú také, ktoré majú aspoň jeden spoločný krajný vrchol. Dve navzájom rôzne hrany, ktoré majú rovnaké krajné vrcholy sa v neorientovanom grafe nazývajú rovnobežné. V orientovanom grafe potom takéto hrany rozlišujeme podľa orientácie na súhlasne rovnobežné a nesúhlasne rovnobežné. Neorientovaný graf je jednoduchý ak v ňom neexistujú žiadne rovnobežné hrany [26].