Algoritmus
Učebné texty
Algoritmus
Algoritmus znamená proces alebo súbor pravidiel ktoré sa majú dodržiavať pri operáciach alebo riešení problémov. Algoritmus sa preto týka súboru pravidiel,pokynov ktoré postupne definujú, ako sa má práca vykonať, aby sa dosiahli očakávané výsledky.[1]
Práca počítača je presne determinovaná. Počítač je absolútne neiniciatívny a všetko, čo chceme, aby urobil mu musíme nariadiť. Prácu počítaču nariaďujeme programom. K tomu aby sme mohli program zostaviť potrebujeme vytvoriť postupnosť krokov, ktorá v každom okamihu určuje ako postupovať ďalej, tzv. algoritmus. Jedna z definícií algoritmu hovorí, že algoritmus je presný popis definujúci výpočtový proces, vedúci od meniteľných vstupných údajov až k žiadaným výsledkom. Táto definícia síce presne vystihuje podstatu a účel algoritmu, je však úzko špecializovaná Obmedzuje sa len na výpočtový proces. Algoritmy však nepoužívame len pri počítačoch pri príprave programov, ale ich použitie je všeobecné. Pomocou algoritmu totiž môžeme presne definovať akýkoľvek determinovaný proces.
Navrhnutý algoritmus je nezávislý od jazyka, tzn. že ide iba o jednoduché pokyny, ktoré je možné implementovať v akomkoľvek jazyku, a napriek tomu bude výstup rovnaký, ako sa očakávalo.
Vlasnosti algoritmu
Jasný a jednoznačný: Každý z jeho krokov by mal byť jasný vo všetkých aspektoch a musí viesť iba k jednému významu.
Dobre definované vstupy:
Algoritmus zvyčajne pracuje s nejakými vstupmi, veličinami, ktoré sú mu odovzdané pred začatím jeho vykonávania, alebo v priebehu jeho činnosti.
Vstupy majú definované množiny hodnôt, ktoré môžu nadobúdať.
Dobre definovaný vstup:
Algoritmus má aspoň jeden výstup, veličinu, ktorá je v požadovanom vzťahu k zadaným vstupom, a tým tvorí odpoveď na problém, ktorý algoritmus rieši.
Efektivita:
Všeobecne požadujeme, aby algoritmus bol efektívny, v tom zmysle, že požadujeme, aby každá operácia požadovaná algoritmom,
bola dostatočne jednoduchá na to, aby mohla byť aspoň v princípe prevedená v konečnom čase iba s použitím ceruzky a papiera.
Všeobecnosť:
Algoritmus nerieši jeden konkrétny problém (napr. „ako vypočítať 3×7“), ale rieši všeobecnú triedu obdobných problémov (napr. „ako vypočítať súčin dvoch celých čísel“).
[2]
Riešenie problému pomocou algorimtu
1. Problém, ktorý má tento algoritmus vyriešiť.
2. Obmedzenia problému, ktoré je potrebné zohľadniť pri jeho riešení.
3. Vstup, ktorý sa má prijať na vyriešenie problému.
4. Výstup, ktorý možno očakávať, keď sa problém vyrieši.
5. Riešenie tohto problému v daných obmedzeniach.[3]
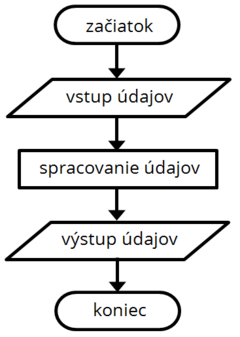
Značky vývojových diagramov
Značka sa využíva na začatie alebo ukončenie vývojového diagramu
Výkonný blok na program
Služi na zápis vstup a výstupov vývojoveého diagramu
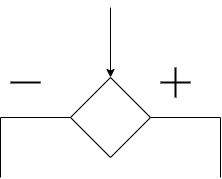
Rozhodovací blok s jedným vstupom a viacerými výstupmi
Spojka
Spojnica
Príklady
Jednoduché opakovanie
Príklad na jednoduché opakovanie
Ak podmienka platí program ide na výstup
Ak je podmienka neplatná vykoná príkaz a znova kým nebude platná podmienka
Príklad na riešenie kvadratickej rovice
Matematický postup riešenia kvadratickej rovnice:
Zistíme diskriminant D = b^2 – 4ac
- ak D > 0, tak daná kvadratická rovnica má 2 rôzne reálne korene
- ak D = 0, tak daná kvadratická rovnica má dva rovnaké reálne korene, čiže tzv. dvojnásobný reálny koreň
- ak D < 0, tak daná kvadratická rovnica nemá riešenie v obore reálnych čísel (samozrejme v obore komplexnýxh čísel má dva imaginárne komplexne združené korene)
potom zisťujeme korene x1,2=(-b ± √D)/2a.
Vývojový diagram pre kvadratickú rovnicu a jej riešenie
Výsledkom diagramu je podla zadaných čísel x1,x2, poprípade x alebo na výstupe bude že nemá riešenie v reálnych čislach
Príklad pomocou vývojového diagramu
Algoritmus, ktorý zistí či je možné zostrojiť trojuholník ak zadáme dĺžky troch strán.
Vstup: Dĺžky strán a,b,c
Výstup: Je možné zostrojiť trojuholník alebo nie.
Rozhodovacie bloky rozhoduju či podmienky su pravdivé