Java - implementácia numerických algoritmov
Základy informatiky - jazyk Java
Úvod do programovania v jazyku Java
Java - objektovo orientovaný prístup
Vzorové príklady:
Java - implementácia numerických algoritmov
- >Java - algoritmy hľadania nulových miest
- >Java - algoritmy numerického derivovania
- >Java - algoritmy numerického integrovania
- >Java - algoritmy aproximácie
- >Java - algoritmy interpolácie
Java - triedy geometrických tvarov
Pokročilé témy:
V nasledujúcej časti budú v krátkosti opísané numerické algoritmy a spôsob ich implementácie v jazyku java, resp. ich použitie v aplikácii a vizualizácia výsledkov. Algoritmy, ktoré budú implementované:
- Algoritmy hľadania nulových miest
- Algoritmy numerickej derivácie
- Algoritmy numerického integrovania
- Algoritmy interpolácie a aproximácie
Pre názornejšiu demonštráciu vysvetľovaných algoritmov budeme tieto výsledky týchto algoritmy vizualizovať v desktopovej java aplikácii.
Obsah
Základné triedy
Trieda Function
Pre reprezentáciu matematickej funkcie si vytvoríme triedu Function. Trieda Function bude teda reprezentovať definovanú matematickú funkciu. Pre náš príklad si zvoľme funkciu:
[math]f\left( x \right)=a\cos \left( b\cdot x \right)-{{x}^{c}}[/math] (1)
kde a, b a c sú parametre našej funkcie. Poznamenajme, že túto funkciu si môžeme ľubovoľne zvoliť.
Samotná trieda Function bude obsahovať len 3 vnútorné premenné: parametre funkcie (1): a, b, c. Výpis triedy Function:
package numeric;
public class Function {
private double a, b, c;
/**
* Konstruktor triedy Function
* Parametre a, b, c definuju koeficienty matematickej funkcie a*cos(b*x)-x^c
* @param a - koficient pri funkcii cos
* @param b - koficient v argumente funkcie cos(b*x)
* @param c - mocnina premennej x v poslednej casti funkcie (x^c)
*/
public Function(double a, double b, double c) {
this.a = a;
this.b = b;
this.c = c;
}
/**
* Implicitny konstruktor.
* definuje funkciu cos(x)-1
*/
public Function() {
this(1, 1, 0);
}
public double getA() {
return a;
}
public double getB() {
return b;
}
public double getC() {
return c;
}
public void setA(double a) {
this.a = a;
}
public void setB(double b) {
this.b = b;
}
public void setC(double c) {
this.c = c;
}
// vrati funkcnu hodnotu v bode x danej matematickej funkcie
public double hodnota(double x) {
return a * Math.cos(b * x) - Math.pow(x, c);
}
}
Trieda Solver
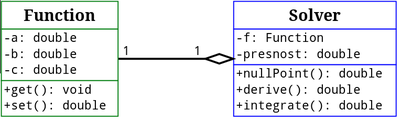
Trieda Function definuje matematickú funkciu nad ktorou budeme implementovať numerické algoritmy. Trieda Solver bude tieto numerické algoritmy implementovať. Trieda Solver bude obsahovať objekt typu Function a premennú presnost, ktorá definuje presnosť výpočtu numerických algoritmov. Tento vzťah ilustruje nasledujúci UML class diagram.
V nasledujúcom texte uvedieme triedu Solver, ktorá bude v nasledujúcich dopĺňanať:
package numeric;
public class Solver {
private Function f;
private double presnost;
/**
* Vytvori objekt triedy solver
* Parameter f je povinny a definuje funkciu (objekt Function)
* nad ktorou sa budu aplikovat numericke algoritmy
* presnost vypoctov je definovana druhym parametrom
* @param f odkaz na existujuci objekt Function
* @param presnost deinuje presnot s akou cheme dostat vysledok zvoleneho
* num. algoritmu. Odporuca sa cislo mensie ako 0.001
*/
public Solver(Function f, double presnost) {
this.f = f;
this.presnost = presnost;
}
/**
* Vytvori objekt triedy solver
* Parameter f je povinny a definuje funkciu (objekt Function)
* nad ktorou sa budu aplikovat numericke algoritmy
* presnost vypoctov je nastavena na 10^(-6), teda na 0.000001
* @param f odkaz na existujuci objekt Function
*/
public Solver(Function f) {
this(f, 0.000001);
}
public Function getF() {
return f;
}
public double getPresnost() {
return presnost;
}
public void setF(Function f) {
this.f = f;
}
public void setPresnost(double presnost) {
this.presnost = presnost;
}
/*
* Tu budu implementovane
* numericke algoritmy
*/
}
Úloha 0: Vykreslenie funkcie f
V úvode tejto kapitoly bolo napísané, že výsledky numerických algoritmov budeme vizualizovať. Ako prvým krokom pri vizualizácii bude zobraziť matematickú funkciu (1). Opäť si tento problém rozdelíme na menšie, ľahko riešiteľné podúlohy. Pri vykresľovaní matematickej funkcie narazíme na nasledujúce problémy:
- potreba pracovať s reálnymi číslami (napr. x=0.01, x=-3.2 a pod.). Avšak pri vykresľovani budeme pracovať len s pixelmi, čo sú kladné celočíselné hodnoty
- samotné vykreslenie funkcie, resp. optimalizované vykreslenie matematickej funkcie.
Ad 1: Trieda Transform
Trieda Transform bude riešiť transformáciu súradníc medzi reálnymi hodnotami, ktoré budeme používať a pixemlmi, ktoré budeme potrebovať pri vykresľovaní. Vysvetlime to podrobnejšie:
- Pre jednoduchosť, majme matematickú funkciu [math]f(x)=x^2[/math]. Uvedieme niektoré hodnoty, s ktorými budeme pracovať:
- x=-1, f(x)=1
- x=-0.5, f(x)=0.23
- x=-0.1, f(x)=0.01
- x=0.1, f(x)=0.01
- x=2.1, f(x)=4.01
- Ak máme určitú oblasť, na ktorú budeme kresliť a táto oblasť má rozmery napr. 300px×300px,
- ako znázorníme bod [-0.5, 0.25] ?
- ako znázorníme bod [0, 0] ?
Potrebujeme teda nejakú transformáciu medzi reálnymi hodnotami a súradnicami v pixeloch, ktré budeme potrebovať pri vykresľovaní. Práve trieda Transform bude vedieť transformovať reálne hodnoty na hodnoty, ktoré použijeme pri vykresľovaní. Na to, aby táto transformácia bola možná, potrebuje mať trieda Transform nasledujúce informácie:
- šírku (width) a výšku (heigth) plochy, na ktorú sa bude kresliť (táto informácie je v pixeloch)
- interval záujmu, na ktorom budeme danú matematickú funkciu vizualizovať. Tento rozsah si označme ako a.
- mierku (scale), ktorú vypočítame z predchádzajúcich údajov.
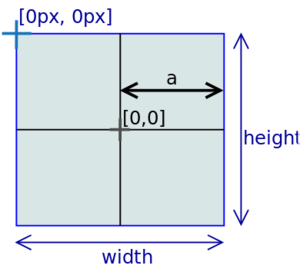
Bližšie to ilustruje nasledujúci obrázok:
Vzťahy použité pre transfomáciu súradníc:
- [math]scale=\frac{width}{2\cdot a}[/math]
- [math]X=x\cdot scale+\frac{width}{2}[/math]
- [math]Y=\frac{height}{2}-y\cdot scale[/math]
kde:
- a definuje interval (0,a), čo je interval pri vykreľovaní. Celý graf je vykresľovaný na intervale (-a, a).
- x,y sú reálne hodnoty, ktoré sú použité pri práci s matematickou funkciou
- X, Y sú celočíselné hodnoty (pixely). Tieto hodnoty využijeme pri vykresľovaní.
- scale je mierka pri vykreľovaní a hovorí o tom koľko pixelov je na intervale <0,1>
- hodnota 1/scale je nazvaná Krok a hovorí akú vzdialenosť predstavuje 1px.
Výpis triedy Transform:
package numeric;
public class Transform {
private int width, height;
private double a;
private double scale;
/**
* konstruktor triedy Transform
* Vytvara triedu pre transformaciu suradnic
* @param s sirka zobrazenia v pixeloch
* @param v vyska zobrazenia v pixeloch
* @param a interval na osi x
*/
public Transform(int s, int v, double a) {
this.width = s;
this.height = v;
this.a = a;
this.scale = this.width / (2 * this.a);
}
/**
* Transormacia v osi x
* @param x hodnota x v realnej suradnicovj sustave
* @return suradnica pre kreslenie (v pixeloch)
*/
public int getX(double x) {
return (int) (x * this.scale) + this.width / 2;
}
/**
* Transormacia v osi y
* @return suradnica pre kreslenie (v pixeloch)
*/
public int getY(double y) {
return this.height / 2 - (int) (y * this.scale);
}
/**
* Mierka scale je pocet pixelov na jednotku dlzky
* Krok je hodnota, ktora pripadne na jeden pixel
* @return krok na jeden pixel
*/
public double getKrok() {
return 1 / this.scale;
}
/**
* Vráti interval kreslenia v kladnej casti osi x
* @return interval a
*/
public double getStrana() {
return this.a;
}
/**
* Nastavi interval kreslenia casti osi x
* @param strana hodnota intervalu <0,a>
*/
public void setStrana(double strana) {
this.a = strana;
// pri zmene intervalu sa meni aj mierka
this.scale = this.width / (2 * this.a);
}
/**
* Nastavi nove rozmery pre vykreslovaciu plochu.
* Mierka vykreslovania (scale) sa prepocita sama
* @param s nova sirka plochy na vykreslovanie
* @param v nova vyska plochy na vykreslovanie
*/
public void setSize(int s, int v) {
this.width = s;
this.height = v;
this.scale = this.width / (2 * this.a);
}
}
Dôležité metódy z tejto triedy:
- public int getX(double x)
- slúži na transformáciu reálnej hodnoty na pixely na osi x. Táto metóda nám odpovie na otázku, na akých súradniciach na osi x je napr bod x=0
- Ak si zoberieme predchádzajúci obrázok, tak bod [0,0] je v strede vykreľovacej plochy. Preto by mal mať bod x=0 hodnotu 1/2 sirky plochy pixelov. Po dosadení do vzťahu transformácie, to naozaj platí.
- public int getY(double y)
- opačné znamienko pri premennej y súvisí s opačnou orientáciou osi y v matematike (y rastie zdola nahor) a v grafike (y rastie zhora nadol).
Ad 2: Vykreslenie matematickej funkcie
Pre vykreslenie matematickej funkcie možeme pokračovať, resp. modifikovať projekt, ktorý bol ukázaný v časti Java (Swing) - práca s vizuálnymi komponentami.
Triedu kiwikiDemo si upravíme nasledovne:
V aplikácii sme teda ponechali len komponent panel (jPanel) a tlačidlo (jButton). Do triedy kiwikiDemo_graf (modifikovaná trieda kiwikiDemo) pridáme nasledujúci kód:
public class kiwikiDemo_graf extends javax.swing.JFrame {
private Graphics g;
private Transform t;
private Function f;
public kiwikiDemo_graf() {
initComponents();
f = new Function();
t = new Transform(panel.getWidth(), panel.getHeight(), 6);
}
// ...
// ...
// ...
}
Teda, do triedy sme pridali objekt t (Transform), ktorý bude slúžiť na výpočet transofrmácie pri vykresľovaní, ďalej obekt f (Function), ktorý nám reprezentuje matematickú funkciu, ktorú budeme vykresľovať. V konštruktore triedy kiwikiDemo_graf tieto objekty vytvoríme.
- Pre objekt f sme použili inplicitný konštruktor, preto bude f reprezentovať matematickú funkciu [math]cos(x)-1[/math].
- Pre objekt transformácie t sme definovali rozmery plochy na kreslenie totožné s rozmermi objektu panel a interval kreslenia <-6, 6>.
Obsluha tlačidla (všetky komentáre sú v zdrojovom kóde):
private void tlcKresliActionPerformed(java.awt.event.ActionEvent evt) {
int sirka, vyska; //sirka a vyska panelu na kreslenie
sirka = panel.getWidth();
vyska = panel.getHeight();
t.setSize(sirka, vyska);
g = panel.getGraphics();
g.setColor(Color.GRAY);
g.drawLine(0, vyska / 2, sirka, vyska / 2);
g.drawLine(sirka / 2, 0, sirka / 2, vyska);
//vykreslovanie matematickej funkcie f
g.setColor(Color.RED);
//realne hodnoty, s ktorymi pocitame
double x1, y1, x2, y2;
//hodnoty v pixelox
int X1, Y1, X2, Y2;
// prvy bod na ose x, ktory sa bude vykreslovat
x1 = -t.getStrana();
y1 = f.hodnota(x1);
for (x2 = -t.getStrana(); x2 < t.getStrana(); x2 += t.getKrok()) {
y2 = f.hodnota(x1);
X1 = t.getX(x1);
X2 = t.getX(x2);
Y1 = t.getY(y1);
Y2 = t.getY(y2);
g.drawLine(X1, Y2, X2, Y2);
x1 = x2;
y1 = y2;
}
}
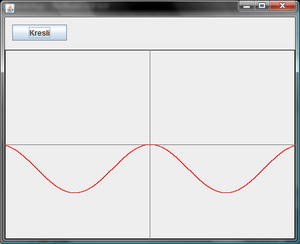
Výsledok: