Softvérové balíky pre riešenie veľkých lineárnych systémov
Softvérové balíky pre riešenie veľkých lineárnych systémov
Riešenie sústav lineárnych rovníc je základom riešenia mnohých problémov vo vedeckých výpočtoch. V mnohých prípadoch sú riešené sústavy veľmi veľké a matica sústavy je riedka. V mnohých aplikáciách je matica symetrická, ako je to napríklad pri použití metódy konečných prvkov. Za posledné desaťročia bolo navrhnutých množstvo nových algoritmov a taktiež programových balíkov pre riešenie symetrických riedkych matíc , ktoré implementujú tieto algoritmy. V tejto časti sú uvedené niektoré balíky obsahujúce priame riešiče riedkych lineárnych systémov.
Priame riešiče riedkych systémov pracujú v niekoľkých fázach. Presné rozdelenie do jednotlivých fáz závisí od použitého algoritmu a softvéru, všeobecné rozdelenie je nasledovné:
- Usporiadanie na základe štruktúry.
- Analýza štruktúry matice na základe, ktorej sa zavedú potrebné dátové štruktúry pre efektívny rozklad matice
- Rozklad matice
- Fáza riešenia, kde sa vykoná eliminácia a potom následne spätná substitúcia.
Fáza rozkladu matice je obvykle časovo najnáročnejšia. Naopak fáza riešenia je všeobecne omnoho rýchlejšia.
Algoritmy rozkladu matíc
Rozklad môže vykonaný rôznymi spôsobmi, čo závisí od prístupu k jednotlivým prvkom systému. Existujú tri základné typy algoritmov : left-looking, right-looking a multifrontal.
Pri right-looking prístupe sa v každom kroku vypočítajú riadky a stĺpce a a tieto zmeny sa hneď aplikujú. Pri left-looking algoritme sa vypočítané zmeny neaplikujú hneď. Predtým ako je eliminovaný stĺpec k , všetky zmeny z predchádzajúcich stĺpcov k matice L sa použijú spolu so stĺpcom k matice A. Pri multifrontálnom algoritme sa zmeny akumulujú, a potom sa aplikujú prostredníctvom tzv. eliminačného stromu.
Niektoré knižnice pre priame riešenie riedkych systémov
PARDISO umožňuje paralelné a sériové riešenie nesymetrických a symetrických riedkych systémov na multiprocesorovom systéme so zdieľanou pamäťou .Využíva sa tu left-looking a right-looking verzia Choleského rozkladu.
SPOOLES je knižnica pre riešenie riedkych reálnych a komplexných sústav rovníc . Je dostupná v paralelnej aj sériovej verzii. Používa sa tu verzia Gaussovej eliminačnej metódy s Croutovou redukciou .
TAUCS je navrhnutá pre symetrické kladne definitné systémy . Používa sa tu left-looking a multifrontálne verzie LU rozkladu a Choleského rozkladu.
UMFPACK je knižnica pre riešenie nesymetrických systémov. Využíva nesymetrický multifrontálny LU rozklad [14].
Simulačný softvér
Existuje viacero softvérov, ktoré používajú metódu konečných prvkov. Pomocou tejto metódy sa transformuje systém parciálnych diferenciálnych rovníc, ktoré popisujú danú úlohu na systém lineárnych rovníc . Táto metóda sa používa v mnohých odvetviach : napr. pri návrhu strojov, rôznych súčiastok, atď.
Pri metóde konečných prvkov sa väčšinou dostávame k veľkému systému lineárnych rovníc . Pre jeho riešenie simulačné softvéry používajú niektoré z uvedených moderných metód . Je známych viacero softvérov ktoré pracujú s metódou konečných prvkov napr. ANSYS, COMSOL, FEMM, ELMER Multiphysics a mnoho ďalších. Pre riešenie vzniknutých veľkých sústav lineárnych rovníc používajú rôzne moderné metódy riešenia. V tab. 1 sú uvedené metódy používané v niektorých simulačných programoch.
Tab. č. 1 Metódy používané v simulačných softvéroch
Ukážkový príklad analýzy vo FEMM
FEMM je softvérový balík pre riešenie nízkofrekvenčných elektromagnetických úloh v 2D. Pre riešenie vzniknutého systému lineárnych rovníc podľa typu riešeného problému používa buď metódu konjugovaných gradientov s prepodmienením alebo metódu bikonjugovaných gradientov [15].
Na (obr.4) je 2D model asynchrónneho motora, pre ktorý hľadáme rozloženie potenciálu.
Obr. 4 Model asynchrónneho motora vo FEMM
Daná úloha má Súbor:Untitled 1 html 49f63057.png stupňov voľnosti, teda sa rieši maticová rovnica s maticou systému o rozmeroch Súbor:Untitled 1 html m3ca83b85.png.
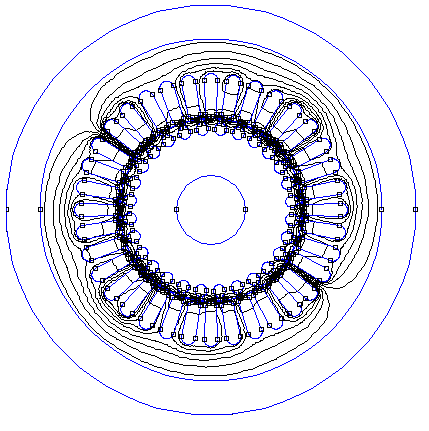Obr. 5 Rozloženie poľa asynchrónneho motora
Na (obr. 5) je vyriešené rozloženie potenciálu pre daný asynchrónny motor. Riešenie danej úlohy metódou bikonjugovaných gradientov prostredníctvom softvéru FEMM trvalo 3 minúty. Riešenie bolo realizované na počítači s procesorom AMD Turion X2 Dual-Core 2.20 GHz a s operačnou pamäťou 4 GB.
