Prehľadávanie do hĺbky

Algoritmy a programovanie

---

Dátový typ

Štruktúry

Rekurzia

Algoritmy vyhľadávania

Algoritmy triedenia

Lineárny zoznam

Binárny strom

Numerické algoritmy

Grafové algoritmy

>Prehľadávanie do šírky
>Prehľadávanie do hĺbky
>Hľadanie najkratšej cesty

Prehľadávanie do hĺbky (anglicky Depth-first search - DFS) je grafový algoritmus, ktorý postupne prechádza všetky metódou backtrackingu. Pracuje tak, že vždy expanduje prvého nasledovníka každého vrcholu, ak ho ešte nenavštívil. Ak narazí na vrchol, z ktorého sa nedá ďalej pokračovať (nemá žiadnych nasledovníkov alebo všetci boli navštívení), vracia sa späť backtrackingom.

Vlastnosti algoritmu

Algoritmus sa snaží o maximálne preskúmanie zvolenej cesty pred prípadnou voľbou ďalšej cesty. Algoritmus je úplný (vždy nájde riešenie, tzn. nájde všetky vrcholy, ktoré sú z východzieho vrcholu dostupné po orientovaných cestách), ale nie je optimálny (pokiaľ graf nieje strom, nemusí nájsť najkratšiu možnou cestu k cieľu).

Využitie algoritmu DFS

Algoritmus prehľadávania do hĺbky sa môže ďalej využívať napríklad pre

• topologické usporiadanie uzlov grafu,
• hľadanie silných komponentov grafu *
• zisťovania acyklickosti grafu,
• riešenie hádaniek s jedným riešením (bludiská) a iné.

Princíp algoritmu DFS

• v grafe začíname od určitého, dopredu stanoveného vrcholu,
• z vrcholu prejdeme k jednému susednému vrcholu, ktorý je s počiatočným vrcholom spojený hranou,
• ak existuje hrana, pokračujeme od susedného vrcholu k ďalšiemu nespracovanému vrcholu atď.,
• ak prídeme do vrcholu, z ktorého sa nedá ísť ďalej, vrátime sa k predchádzajúcemu vrcholu a od neho skúsime pokračovať v prehľadávaní grafu,
• aby sme rozlíšili tie vrcholy, ktoré sme už spracovali od tých, ktoré sme ešte nenavštívili a nespracovali, máme v každom vrchole stavovú položku znacky:
  • na začiatku zabezpečíme, aby mali všetky vrcholy nastavenú položku znacky na hodnotu 0,
  • postupne, ako budeme vrcholy navštevovať, budeme týmto vrcholom nastavovať znacky na hodnotu 1,

prechádzanie do hĺbky vyzerá tak, akoby sme sa v grafe rozbehli po hranách ďaleko od počiatočného vrcholu a vrcholy krížom-krážom ponavštevovali vrcholy grafu.

Implementácia algoritmu DSF

Pseudokód

Počiatočný vrchol: v. TRASA – zásobník (FIFO).

1. TRASA={0}, označkujeme v
2. Vyber ľubovoľnú hranu e začínajúcu vo vrchole v. Ak taká existuje tak =>3, ak neexistuje =>5
3. Označ w ako koncový vrchol vybranej hrany. Ak je w označkovaný, tak =>2, inak =>4
4. Hranu e pridáme do zoznamu TRASA. Dosadíme v=w. Označkujeme v. choď => 2
5. Ak je TRASA neprázdny odober z konca hranu e a jej počiatočný vrchol označ v. Choď => 2
6. Ak je TRASA prázdny, tak koniec.

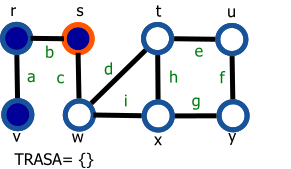
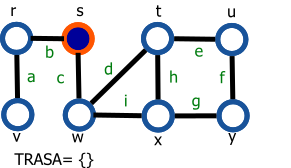
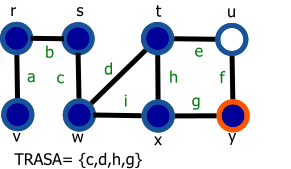
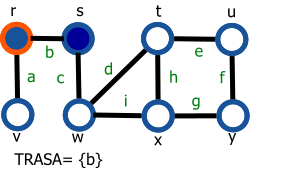
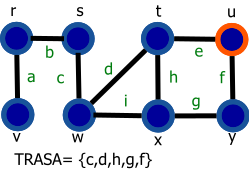
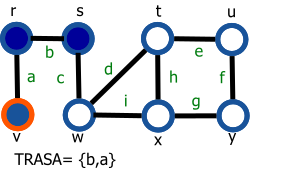
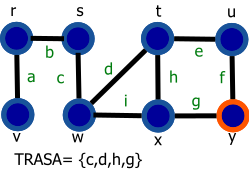
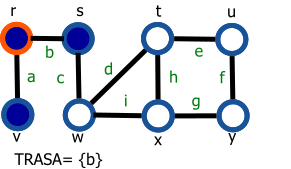
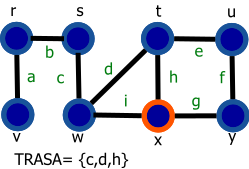
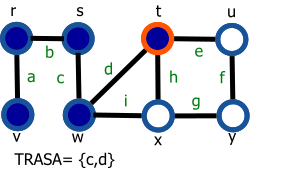
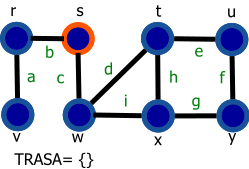
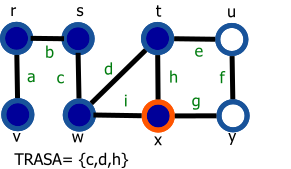
Ukážka k predchádzajúcemu pseudokódu: Na nasledujúcich obrázkoch bude ukážka algoritmu DFS. Graf je daný nasledovne: G=(V,E), V={r,s,t,u,v,w,x,y}, E={a,b,c,d,e,f,g,h,i}.

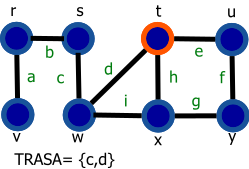
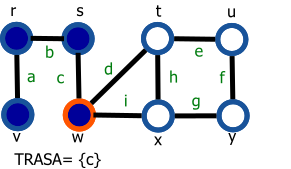
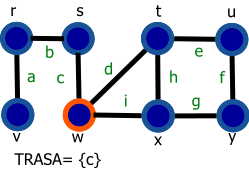
Vrchol s modrou výplňou reprezentuje navštívený vrchol a vrchol s oranžovým okrejom reprezentuje aktuálny vrchol (vrchol 'v' z preudokódu).

1. Začíname vo vrchole s	9. Označíme vrchol y a hranu g pridáme do zoznamu TRASA
2. Označíme vrchol r a hranu b pridáme do zoznamu TRASA	10. Označíme vrchol u a hranu f pridáme do zoznamu TRASA
3. Označíme vrchol v a hranu a pridáme do zoznamu TRASA	11. Nie je možné označiť žiadnu ďalšiu hranu. Preto odoberieme zo zoznamu FRONTA hranu f.
4. Nie je možné označiť žiadnu ďalšiu hranu. Preto odoberieme zo zoznamu FRONTA hranu a.	12. Nie je možné označiť žiadnu ďalšiu hranu. Preto odoberieme zo zoznamu FRONTA hranu g.
5. Nie je možné označiť žiadnu ďalšiu hranu. Preto odoberieme zo zoznamu FRONTA hranu b.	13. Nie je možné označiť žiadnu ďalšiu hranu. Preto odoberieme zo zoznamu FRONTA hranu h.
6. Označíme vrchol w a hranu c pridáme do zoznamu TRASA	14. Nie je možné označiť žiadnu ďalšiu hranu. Preto odoberieme zo zoznamu FRONTA hranu d.
7. Môžeme označiť vrcholy t a x. Výber vrcholu je náhodný. Označíme vrchol t a hranu d pridáme do zoznamu TRASA	15. Nie je možné označiť žiadnu ďalšiu hranu. Preto odoberieme zo zoznamu FRONTA hranu c.
9. Môžeme označiť vrcholy u a x. Výber vrcholu je náhodný. Označíme vrchol x a hranu h pridáme do zoznamu TRASA	16. Koniec algoritmu. Všetky vrcholy sú označené a sme vo východzom vrchole.

Kód v jazyku C

Pri implementácii algoritmu DFS v jazyku C namiesto dátovej štruktúry FIFO využijeme mechanizmus rekurzie. Pri rekurzívnom volaní funkcie sa stav (kontext) vo funkcii uložia do zásobníka. Túto skutočnosť využijeme ako náhradu dátovej štruktúry FIFO.

Opis funkčného prototypu:

int **graf: maticová reprezentácia grafu.

int n: počet vrcholov grafu graf.

int znacky[]: pole, v ktorom uchovávame navštívené vrcholy.

int i: počiatočný vrchol

 1 void dfs(int **graf,int znacky[],int n,int i)
 2 {
 3    znacky[i]=1;
 4    for(int k=0;k<n;k++)
 5    {   
 6       if(graf[i][k]!=0)
 7       {
 8           if(znacky[k]==0)
 9           {
10              cout<<k<<" ";
11              dfs(graf,znacky,n,k);
12              cout<<"."<<endl;
13           }
14      }
15   }
16 }

Komentáre ku zdrojovému kódu:

• Riadok 1: Začíname vo vrchole i
• Riadok 3: Vrchol i si označíme ako navštívený
• Riadok 4: Prechádzame cez všetky vrcholy grafu.
• Riadok 6: Hľadáme taký vrchol k, ktorý je susedom vrcholu i
• Riadok 5: Ak nebol susedný vrchol vrcholu i (vrchol k) ešte označkovaný, tak
• Riadok 10: Výpis, ktorý vrchol sme označili.
• Riadok 11: Rekurzívne volaná funkcie dfs. Východzí vrhol bude k.
• Riadok 12: Po skončení rekurzívneho volania vypíšeme "." - vracanie sa naspäť.