Náhodná premenná, funkcia hustoty, distribučná funkcia, vlastnosti, číselné charakteristiky náhodnej premennej

Tento článok patrí do časti Kolokviálna skúška. Materiály tu uvedené sú prípravou na záverečnú štátnu (kolokviálnu) skúšku v študijnom zameraní Manažérstvo kvality produkcie na Fakulte mechatroniky TnUAD.

Náhodná premenná

Náhodný jav - je jav ktorý ako výsledok určitého pokusu (komplexu podmienok) môže alebo nemusí nastať. Označujeme veľkými písmenami zo začiatku abecedy A,B,C.... Extrémnymi prípadmi javov je : jav istý a jav nemožný. Jav istý (I)je taký jav ktorý ako výsledok daného pokusu nastane vždy. Jav nemožný (O)je taký jav ktorý ako výsledok pokusu nemôže nastať nikdy. Pravdepodobnosť je číselná miera možnosti nastatia náhodného javu

Náhodný jav charakterizuje výsledok náhodného pokusu kvalitatívne (slovne). V mnohých prípadoch je však výhodnejšie charakterizovať výsledok kvantitatívne (číselne), k čomu používame náhodnú premennú.

Náhodná premenná- taká premenná, ktorá môže nadobúdať rôzne hodnoty, alebo hodnoty z rôznych intervalov v závislosti na náhode. Náhodné veličiny budeme označovať veľkými písmenami s konca abecedy X,Y,Z a ich konkrétne hodnoty: xj, j=1,2…n

Na štatistické znaky môžme pozerať ako na náhodné premenné NP

Členenie NP: diskrétne (DNP) -nadobúdajú izolované, väčšinou celočíselné hodnoty, napr. počet narodených chlapcov z 1000 narodených detí, počet chybných výrobkov

spojité (SNP)-môžu nadobúdať ľubovoľné hodnoty z ohraničeného, alebo neohraničeného intervalu, napr.: hmotnosť, výška človeka, chyby merania v mm, príjem...

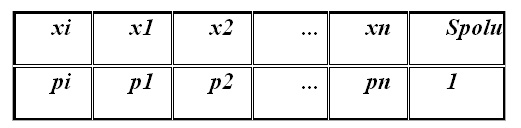
Pravdepodobnostná tabuľka - rad rozdelenia pravdepodobností - popisuje len diskrétnu náhodnú premennú (DNP), je najjednoduchšou formou zákona rozdelenia

Distribučná funkcia je univerzálnejšou formou vyjadrenia zákona rozdelenia, slúži k popisu tak diskrétnej ako aj spojitej NP. Každému reálnemu číslu priraďuje pravdepodobnosť, že NP nadobudne hodnotu menšiu než toto číslo tj.:

F(x) = P(X £ x)

Vlastnosti distribučnej funkcie