Hľadanie najkratšej cesty: Rozdiel medzi revíziami

Z Kiwiki
Skočit na navigaci Skočit na vyhledávání
d
 
Riadok 1: Riadok 1:
−
[[Kategória:Študijné materiály]]
+
[[Kategória:Grafové algoritmy]]
−
[[Kategória:Programovanie]]
 
−
[[Kategória:Informatika]]
 
−
[[Kategória:Teória grafov]]
 
 
{{Draft}}
 
{{Draft}}
 
{{Skripta programovanie}}
 
{{Skripta programovanie}}

Aktuálna revízia z 22:22, 16. august 2010

Imbox draft.png
 Toto je projekt, na ktorom sa ešte stále pracuje!!

Aj keď sú v tomto dokumente použiteľné informácie, ešte nie je dokončený. Svoje návrhy môžete vyjadriť v diskusii o tejto stránke.

Algoritmy a programovanie

Dátový typ

Štruktúry

Rekurzia

Algoritmy vyhľadávania

Algoritmy triedenia

Lineárny zoznam

Binárny strom

Numerické algoritmy

Grafové algoritmy

>Prehľadávanie do šírky
>Prehľadávanie do hĺbky
>Hľadanie najkratšej cesty

Medzi algoritmy hľadajúce najkratšie cesty medzi vrcholmi grafu patria:

Floyd–Warshallov algoritmus
používa sa pre nájdenie najkratšej cesty v orientovanom grafe s hranami, ktoré majú rôzne váhy. Jediný priechod algoritmu spočíta najkratšiu cestu medzi všetkými dvojicami vrcholov. Floyd–Warshallov algoritmus je typickým príkladom dynamického programovania [1].
Dijkstrov algoritmus 
je jedným zo základných algoritmov teórie grafov, jeho primárnym využitím je hľadanie najkratšej cesty v hranovo-ohodnotenom digrafe G = (V, H, c). Tento graf pozostáva z množiny vrcholov V, množiny orientovaných hrán H a funkcie c, ktorá zobrazuje množinu hrán do množiny reálnych čísel. Teda pre ňu platí H → R. Ďalším predpokladom je aby c(h) ≥ 0, pre všetky hrany h z množiny H. Jeho autorom je holandský matematik E. W. Dijkstra a typovo ide o algoritmus najkratšej cesty z jedného vrcholu (počiatok, označme ho aj s) do ostatných, najčastejšie však do jedného konkrétneho (cieľ d)[2].
Johnsonov algoritmus
hľadá najkratšiu cestu medzi všetkými dvojicami vrcholov v riedkom orientovanom grafe. Algoritmus dovoľuje, aby mali niektoré hrany zápornú hodnotu. Hrany, ktoré sa nachádzajú v cykle, nemôžu mať zápornú hodnotu. Algoritmus pracuje na základe Belmann-Fordovho algoritmu, ktorý vypočíta transformáciu vstupného grafu, aby sa odstránili záporné hodnoty hrán. Pre výpočet najkratších ciest v tomto transformovanom grafe sa používa Dijkstrov algoritmus.[3]

Floyd–Warshallov algoritmus

Floyd–Warshallov algoritmus porovnáva všetky možné cesty v grafe medzi všetkými dvojicami vrcholov. Pracuje tak, že postupne vylepšuje odhad na najkratšiu cestu potiaľ, až je zrejmé, že odhad je optimálny.

Princíp algoritmu

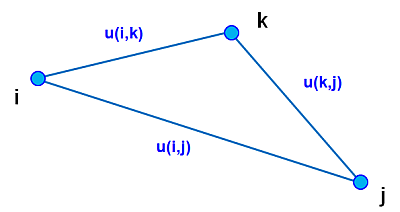
Celý princíp hľadania najkratšej cesty je postavený na elementárnej nerovnosti: Uvažujme ľubovoľný trojuholník ijk. Platí, že cesta z i do j je určite kratšia ako z i do k a z k do j.

Trojuholníková nerovnosť

Pre trojuholník ijk platí:

[math]u\left( i,j \right)\le u\left( i,k \right)+u\left( k,j \right)[/math]

kde u(i,j) znamená hrana z vrcholu i do vrcholu j.

Podmienkou pre nájdenie všetkých najkratších ciest je, že v grafe nesmie existovať cyklus v ktorom je hrana so zápornou hodnotou.

Pri hľadaní najkratšej cesty začíname zo známymi vzdialenosťami v grafe. Ak pre 2 vrcholy v grafe G poznáme ich vzdialenosť, pokúsime sa do cesty medzi tieto dva vrcholy vložiť iný vrchol, ktorý by mohol cestu vylepšiť (pre tento vrchol nebude platiť trojuholníková nerovnosť).

Príprava vstupných údajov

Majme graf G, ktorý je opísaný maticou susednosti vrcholov [math]M_g[/math]. Túto maticu si pretransformujeme na maticu vzdialeností [math]W_G[/math] nasledovne:

  • [math]w(i,i)=0[/math]
  • [math]w(i,j)=vzdialenosť(i,j)[/math], ak je medzi i a j hrana
  • [math]w(i,j)=\infty [/math], ak medzi i a j nie je hrana

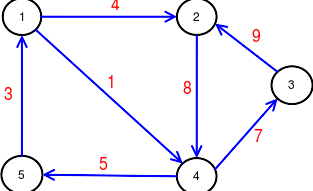
Pre graf

graf G

je matica susednoti:

[math]{{M}_{G}}=\left( \begin{matrix} 0 & 4 & 0 & 1 & 0 \\ 0 & 0 & 0 & 8 & 0 \\ 0 & 9 & 0 & 0 & 0 \\ 0 & 0 & 7 & 0 & 5 \\ 3 & 0 & 0 & 0 & 0 \\ \end{matrix} \right)[/math]
 (1)

a matica nakratších ciest:

[math]{{W}_{G}}=\left( \begin{matrix} 0 & 4 & \infty & 1 & 3 \\ 4 & 0 & 9 & 8 & \infty \\ \infty & 9 & 0 & 7 & 0 \\ 1 & 8 & 7 & 0 & 5 \\ 3 & \infty & \infty & 5 & 0 \\ \end{matrix} \right)[/math]
 (2)

Pseudokód

Algoritmus pracuje s maticou najkratších ciest W. Hranu, resp. cestu medzi vrcholmi i a j budeme označovať u(i,j).

Princíp funkčnosti

  1. Pre všetky kombinácie vrcholov i, j grafu G:
  2. Do cesty u(i,j) pridaj ľubovoľný vrchol k. (postupne budeme skúšať všetky vrcholy)
  3. Ak platí: [math]u\left( i,j \right)\ge u\left( i,k \right)+u\left( k,j \right)[/math] tak 4
  4. [math]u\left( i,j \right)= u\left( i,k \right)+u\left( k,j \right)[/math]

Preudokód 

 1 funkcia FloydWarshall ()
 2 cesta[][] // dvojrozmerné pole - matica najkratších ciest.
 3  pre vsetky k: k = 1 .. N
 4    begin
 5     pre každú dvojicu (i,j) z množiny vrcholov (1..N)
 6     begin
 7        cesta[i][j] = min(cesta[i][j], cesta[i][k] + cesta[k][j]);
 8     end
 9  end
10 endproc

Ukážkový príklad

Majme graf G, ktorého maticu najkratších ciest opisuje vzorec 2.

  • Hľadáme cestu z vrholu 1 do vrcholu 3. Hodnota v matici W je nekonečno. [math]w(i,j)=\infty[/math]
  • Do cesty sa pokúsime pridať vrchol k=2. Platí teda: w(1,3)>w(1,2)+w(2,3)
  • Vrchol k vylepší cestu, teda ho do cesty zaradíme
    • w(1,3)=4+9=13
[math]{{W}_{G}}=\left( \begin{matrix} 0 & 4 & 13 & 1 & 3 \\ 4 & 0 & 9 & 8 & \infty \\ \infty & 9 & 0 & 7 & 0 \\ 1 & 8 & 7 & 0 & 5 \\ 3 & \infty & \infty & 5 & 0 \\ \end{matrix} \right)[/math]
  • Skúsme do cesty pridať vrchol k=4:
    • w(1,3)>w(1,4)+w(4,3)
  • Vrchol k vylepší cestu, teda ho do cesty zaradíme
    • w(1,3)=1+7=8
[math]{{W}_{G}}=\left( \begin{matrix} 0 & 4 & 8 & 1 & 3 \\ 4 & 0 & 9 & 8 & \infty \\ \infty & 9 & 0 & 7 & 0 \\ 1 & 8 & 7 & 0 & 5 \\ 3 & \infty & \infty & 5 & 0 \\ \end{matrix} \right)[/math]

Implementácia v jazyku C

1 void floyd(int **W,int pocetV)
2 {
3  int i,j,k;
4  for(k=0 ; k<pocetV ; k++) 
5     for(i=0 ; i<pocetV ; i++) 
6         for(j=0 ; j<pocetV ; j++)
7             W[i][j]=min(W[i][j] , W[i][k]+W[k][j]);
8 }

Opis kódu:

  • W: matica najkratších ciest
  • pocetV: rozmer matice W (počet vrcholov grafu)

Modifikácia algoritmu

  • Navrhnutý algoritmus síce zistí najkratšiu cestu, ale nepamätá si cestu.

Pre uloženie si vrcholov, ktoré vylepšili pôvodnú cestu medzi hranami grafu si vytvorme maticu navrhnutých ciest R.

Hodnoty matice R:

  • [math]r(i,j)=0[/math], ak sú vrholy i a j susedné
  • [math]r\left( i,j \right)=k[/math], ak [math]w\left( i,k \right)+w\left( k,j \right)\lt w\left( i,j \right)[/math] - teda ak vrchol k vylepšil cestu z i do j.

Matice navrhnutých ciest pre graf G je nasledovná:

[math]{{R}_{G}}=\left( \begin{matrix} 0 & 0 & 4 & 0 & 4 \\ 5 & 0 & 4 & 0 & 4 \\ 5 & 0 & 0 & 2 & 4 \\ 5 & 5 & 0 & 0 & 0 \\ 0 & 1 & 4 & 1 & 0 \\ \end{matrix} \right)[/math]

Vysvetlime si riadok význam prvkov na pre najkratšiu cestu z vrcholu 3 do vrcholu 1. Jedná sa teda o prvok matice R(3,1)

  • R(3,1)=5: cesta z 3 do 1 ide cez vrchol 5. Hľadáme teda cestu z 3 do 5.
  • R(3,5)=4: cesta z 3 do 5 ide cez vrchol 4. Hľadáme teda cestu z 3 do 4.
  • R(3,4)=2: cesta z 3 do 4 ide cez vrchol 2. Hľadáme teda cestu z 3 do 2.
  • R(3,2)=0: vrcholy 3 a 2 sú susedné.

Implementácia v jazyku C

 1 void floyd2(int **M,int **R,int r)
 2 {
 3  int i,j,k;
 4  for(k=0;k<r;k++) 
 5     for(i=0;i<r;i++) 
 6        for(j=0;j<r;j++)
 7           if(M[i][j]>M[i][k]+M[k][j])
 8           {
 9              M[i][j]=M[i][k]+M[k][j];
10              R[i][j]=k+1;
11           }
12 }

Opis kódu:

  • M: matica najkratších ciest
  • R: matica navrhnutých ciest
  • r: rozmer matice W (počet vrcholov grafu)
  • Poznámka: v riadku 10 priraďujeme do matice R hodnoty k+1 z toho dôvodu, pretože vrcholy v grafe sú označené 1..n, ale vnútorná reprezentácia je 0..n-1.

Pre výpis matice najkratších ciest si vytvoríme funkciu, ktorá z matice R zistí navrhovanú cestu. Funkcia bude mať 3 parametre: maticu R, vrchol i a vrchol j. Ak je v matici na indexe i,j hodnota rôzna od nuly, znamená to že medzi vrcholmi je cesta (i,k) a (k,j). Na zabezpečenie takéhoto výpisu využijeme mechanizmus rekurzie. Rekurzívne volanie sa skončí vtedy, keď R[i][j]=0. 

 1 void cesta(int **R,int i,int j)  // vypíše cestu z i do j
 2 {
 3   int k=R[i][j]; 
 4   if(k!=0)
 5   {     //pozn: k-1 je uvedene kvoli vnutornej reprezentacii vrcholov
 6         cesta(R,i,k-1);  // cesta z i do k
 7         cout<<k<<" ";    // vypis, kadial vedie cesta
 8         cesta(R,k-1,j);  // cesta z k do j
 9   } 
10 }

Opis kódu:

  • R: matica navrhnutých ciest
  • i: vrchol i
  • j: vrchol j.
  • Poznámka: V príklade máme vrcholy označené 1..n. Vo vnútornej reprezentácii (matica M) sú označené ako 0..n-1, do funkcie cesta musíme použiť číslovanie vrcholov podľa vnútornej reprezentácie. Aby sme sa tomuto vyhli, vytvoríme si funkciu, ktorá nám tento "prevod" zabezpečí.
1 void Cesta(int **R,int i,int j)
2 {   
3     cout<<"cesta z "<<i<<" do "<<j<<": ";
4     cout<<i<<" ";
5     cesta(R,i-1,j-1);
6     cout<<j<<" "<<endl;
7 }

Vzorové výstupy programu

Výpis všetkých matíc použitých v príklade:

[math]{{W}_{G}}=\left( \begin{matrix} 0 & 4 & 8 & 1 & 6 \\ 16 & 0 & 8 & 15 & 13 \\ 25 & 9 & 0 & 17 & 22 \\ 1 & 12 & 7 & 0 & 5 \\ 3 & 7 & 11 & 4 & 0 \\ \end{matrix} \right)[/math]
[math]{{R}_{G}}=\left( \begin{matrix} 0 & 0 & 4 & 0 & 4 \\ 5 & 0 & 4 & 0 & 4 \\ 5 & 0 & 0 & 2 & 4 \\ 5 & 5 & 0 & 0 & 0 \\ 0 & 1 & 4 & 1 & 0 \\ \end{matrix} \right)[/math]

Výpisy najkratších navrhnutých ciest: 

cesta z 1 do 2: 1 2 
cesta z 1 do 3: 1 4 3 
cesta z 1 do 4: 1 4 
cesta z 1 do 5: 1 4 5 
cesta z 2 do 1: 2 4 5 1 
cesta z 2 do 3: 2 4 3 
cesta z 2 do 4: 2 4 
cesta z 2 do 5: 2 4 5 
cesta z 3 do 1: 3 2 4 5 1 
cesta z 3 do 2: 3 2 
cesta z 3 do 4: 3 2 4 
cesta z 3 do 5: 3 2 4 5 
cesta z 4 do 1: 4 5 1 
cesta z 4 do 2: 4 5 1 2 
cesta z 4 do 3: 4 3 
cesta z 4 do 5: 4 5 
cesta z 5 do 1: 5 1 
cesta z 5 do 2: 5 1 2 
cesta z 5 do 3: 5 1 4 3 
cesta z 5 do 4: 5 1 4

Dijkstrov algoritmus

Johnsonov algoritmus

Zdroje a odkazy

  1. ↑ http://cs.wikipedia.org/wiki/Floyd%C5%AFv-Warshall%C5%AFv_algoritmus
  2. ↑ http://sk.wikipedia.org/wiki/Dijkstrov_algoritmus
  3. ↑ http://en.wikipedia.org/wiki/Johnson%27s_algorithm
Zdroj: „http://www.kiwiki.info/index.php?title=Hľadanie_najkratšej_cesty&oldid=6664“