Hromada: Rozdiel medzi revíziami
(Vytvorená stránka „Kategória:Študijné materiály Kategória:Programovanie Kategória:Informatika {{Draft}} {{Skripta programovanie}} ==Hromada== Hromada (Halda) je stromová d…“) |
|||
| Riadok 38: | Riadok 38: | ||
*Pravý potomok uzla – x[i*2+1] | *Pravý potomok uzla – x[i*2+1] | ||
*Index otca vrholu i - <math> \left \lfloor i/2 \right \rfloor</math> | *Index otca vrholu i - <math> \left \lfloor i/2 \right \rfloor</math> | ||
| + | |||
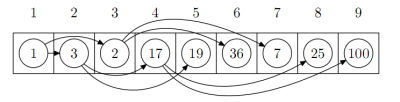
| + | Reprezentácia hromady pomocou jednorozmerného poľa: | ||
| + | [[Súbor:heap1.png|center|framed|usporiadanie prvkov hromady]] | ||
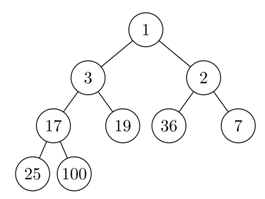
| + | [[Súbor:heap2.png|center|framed|binárna hromada]] | ||
Pri implementácie hromady pomocou jednorozmerného poľa pracujeme od indexu 1!!! | Pri implementácie hromady pomocou jednorozmerného poľa pracujeme od indexu 1!!! | ||
| Riadok 54: | Riadok 58: | ||
* ''n'' - aktuálna veľkosť hromady. | * ''n'' - aktuálna veľkosť hromady. | ||
| + | '''Pomocné funkcie pre prácu s hromadou:''' | ||
| + | ;BubbleUp:Zabezpečí prebublanie ľahkých prvkov smerom hore | ||
| + | ;BubbleDown:Zabezpečí prebublanie ťažkých prvkov smerom dole | ||
| + | |||
| + | Prebublávanie funguje podobne ako pri bublinkovom triedení. | ||
| + | Na rozdiel od Bubblesort, prebublávame pozdĺž cesty vedúcej od uzlu v po koreň stromu | ||
| + | |||
| + | ====Pseudokódy==== | ||
| + | Poznámka ku pseudokódom: výraz k/2 (n/2) je celočíselné delenie. | ||
| + | <source lang="pascal" line> | ||
| + | BubbleUp(k) | ||
| + | pokiaľ k>1 a x(k/2)>x(k) rob | ||
| + | zamen(k, k/2) | ||
| + | k= k/2 | ||
| + | |||
| + | BubbleDown(k) | ||
| + | pokiaľ k<=n/2 rob | ||
| + | min=2k // inicializacia | ||
| + | ak 2k+1 <= n a x(2k)> x(2k+1) tak | ||
| + | min=2k+1 | ||
| + | ak x(min) < x(k) tak | ||
| + | zamen(k,min) | ||
| + | inak | ||
| + | break | ||
| + | k=min | ||
| + | |||
| + | Min | ||
| + | return x[1] | ||
| + | |||
| + | Delete_min | ||
| + | x[1]=x[n] | ||
| + | n=n-1 | ||
| + | BubbleDown(n) | ||
| + | |||
| + | Insert(h) | ||
| + | n=n+1 | ||
| + | x[n]=h | ||
| + | BubbleUp(n) | ||
| + | |||
| + | Delete(k) | ||
| + | tmp=x[k] | ||
| + | x[k]=x[n] | ||
| + | n=n-1 | ||
| + | ak tmp<=x[k] | ||
| + | BubbleDown(k) | ||
| + | inak | ||
| + | BubbleUp(k) | ||
| + | |||
| + | </source> | ||
| + | '''Vymazanie prvku s minimálnou hodnotou - Delete_min''' | ||
| + | |||
| + | Vieme, že v hromade je prvok s minimálnou hodnotou vždy na indexe 1. Tento prvok vymažeme a na jeho miesto umiestnime posledný prvok v poli (riadok 21). Tým pádom sa nám zmenší počet prvkov v poli o 1 (riadok 22). Na indexe 1 je prvok z konca poľa. Tento prvok musíme umiestniť na správne miesto pomocou procedúry BubbleDown (riadok 23). | ||
| + | |||
| + | '''Vloženie nového prvku na hromadu - Insert(n)''' | ||
| + | |||
| + | Pole zväčšíme o 1 prvok (riadok 26). Do tohoto nového prvku, ktorý je na konci poľa vložíme daný prvok (riadok 27). Tento prvok umiestnime na správen miesto pomocou procedúry BubbleUp (riadok 28) | ||
| + | |||
| + | '''Vymazanie prvku s na určitim indexe k - Delete''' | ||
| + | |||
| + | Mažeme prvok na indexe k. Na jeho miesto môžeme umiestniť prvok z konca poľa (riadok 32). Tým sa nám zmenší počet prvkov hromady o 1 (riadok 33). Podľa toho či prvok, ktorý sme vymazali (tmp - riadok 31) bol väčší alebo menší ako poslendý prvok (aktuálne na pozícii k - riadok 34) použijeme procedúru BubbleDown (riadok 35) alebo BubbleUp (riadok 37) | ||
| + | |||
| + | ====Implementácia v jazyku C==== | ||
| + | <source lang="c" line> | ||
| + | #include <iostream.h> | ||
| + | #define MAX_HEAP 100 | ||
| + | |||
| + | struct Hromada | ||
| + | { int data[ MAX_HEAP]; | ||
| + | int n; | ||
| + | }; | ||
| + | |||
| + | void zamen(Hromada &H,int k, int k2) | ||
| + | { | ||
| + | int tmp=H.data[k]; | ||
| + | H.data[k]=H.data[k2]; | ||
| + | H.data[k2]=tmp; | ||
| + | } | ||
| + | |||
| + | void BubbleUp(Hromada &H, int k) | ||
| + | { | ||
| + | while(k>1 && H.data[k/2]>H.data[k]) | ||
| + | { | ||
| + | zamen(H,k,k/2); | ||
| + | k/=2; | ||
| + | } | ||
| + | } | ||
| + | |||
| + | void BubbleDown(Hromada &H, int k) | ||
| + | { | ||
| + | int min; | ||
| + | while(k<= H.n/2) // ak je k potomok lub. uzla | ||
| + | { | ||
| + | min=2*k; // zitim ktory z dvoch potomkov uzla k je mensi | ||
| + | if( (2*k+1)<=H.n && H.data[2*k]>H.data[2*k+1]) | ||
| + | min=2*k+1; | ||
| + | if(H.data[min]<H.data[k]) // prebublavanie dole | ||
| + | zamen(H,k,min); | ||
| + | else | ||
| + | break; | ||
| + | k=min; | ||
| + | } | ||
| + | } | ||
| + | void push(Hromada &H, int hodnota) | ||
| + | { | ||
| + | H.n++; | ||
| + | H.data[H.n]=hodnota; | ||
| + | BubbleUp(H,H.n); | ||
| + | } | ||
| + | |||
| + | int pop(Hromada &H) | ||
| + | { | ||
| + | int x=H.data[1]; | ||
| + | H.data[1]=H.data[H.n]; | ||
| + | H.n--; | ||
| + | BubbleDown(H,1); | ||
| + | return x; | ||
| + | } | ||
| + | int Delete(Hromada &H, int k) | ||
| + | { | ||
| + | int val=H.data[k]; | ||
| + | H.data[k]=H.data[H.n]; | ||
| + | H.n--; | ||
| + | if( val < H.data[k]) | ||
| + | BubbleDown(H,k); | ||
| + | else | ||
| + | BubbleUp(H,k); | ||
| + | return val; | ||
| + | } | ||
| + | void vypis(Hromada H) | ||
| + | { | ||
| + | for(int i=1;i<=H.n;i++) | ||
| + | cout<<H.data[i]<<" "; | ||
| + | cout<<endl; | ||
| + | } | ||
| + | int main() | ||
| + | { | ||
| + | Hromada heap; | ||
| + | heap.n=0; | ||
| + | push(heap,10); | ||
| + | push(heap,9); | ||
| + | push(heap,8); | ||
| + | push(heap,7); | ||
| + | push(heap,6); | ||
| + | push(heap,3); | ||
| + | |||
| + | vypis(heap); | ||
| + | |||
| + | int x=pop(heap); | ||
| + | cout<<"Vybral som min: "<<x<<endl; | ||
| + | vypis(heap); | ||
| + | |||
| + | cout<<"Mazem prvok s indexom 3: "<<endl; | ||
| + | Delete(heap,3); | ||
| + | vypis(heap); | ||
| + | } | ||
| + | </source> | ||
==Zdroje== | ==Zdroje== | ||
| + | *http://algoritmicke-techniky.sk/zaciatocnik/1-4-Prioritna_fronta.html | ||
| + | *http://en.wikipedia.org/wiki/Heap_%28data_structure%29 | ||
<references/> | <references/> | ||
Verzia zo dňa a času 22:57, 14. marec 2010
Obsah
Hromada
Hromada (Halda) je stromová dátová štruktúra, ktorá spĺňa dve podmienky[1]:
- Lokálnu podmienku na usporiadanie, ktorá vyžaduje, aby pre každý uzol stromu platilo, že prvok, ktorý reprezentuje, je menší ako prvok reprezentovaný jeho potomkami.
- Štrukturálnu podmienku na to, ako strom vyzerá - líši sa podľa jednotlivých typov háld.
Lokálna podmienka môže byť položená aj opačne: predok môže reprezentovať prvky väčšie ako potomkovia.
Problém pri reprezentácii haldy polom nastane vtedy, keď budeme chcieť z tohto pola mazať prvky, čo trvá príliš dlhý čas, teda je to neefektívne. Pre efektívnejšiu implementáciu bola vymyslená binárna halda. Príklad binárnej haldy:
Binárna hromada
Je to úplný binárny strom v ktorom priorita všetkých vrcholov je väčšia ako jeho potomkov. Úplný binárny strom znamená, že dĺžka cesty od koreňa do každého listu je rozdielna maximálne o 1. Preto v tomto type dátovej štruktúry trvá každá cesta najviac O(log n), kde n je počet prvkov. Jednoduché operácie na binárnej halde trvajú log n. Najčastejšie operácie na halde sú:
- DELETE-MAX - MAX vymaže prvok s najväčšou prioritou
- INCREASE-KEY - zvýši prioritu prvku buď o 1, alebo o určitú hodnotu, podľa toho, ako je to implementované.
- INSERT - vloží prvok do binárnej haldy
- MERGE - spojí dve haldy do jednej novej správne usporiadanej haldy obsahujúca všetky prvky oboch spájaných háld.
Využitie hromady
Prioritná fronta, inak povedané prioritný rad. Je to také usporiadanie prvkov či operácií, že prvky majú ohodnotenie svojej priority, najčastejšie číslom. Podstatné je, aby sme mali v tejto fronte najväčší prvok na začiatku fronty a usporiadanie ostatných prvkov nás ani tak veľmi nezaujíma. To je aj hlavný rozdiel prioritného radu od obyčajného radu. Z toho plynú najčastejšie operácie: pridanie nového prvku, odstránenie najväčšieho.
Dijkstrov algoritmus
Implementácia hromady v jazyku C
Návrh vhodnej dátovej štruktúry
Pre jednoduchosť budeme vytvárať hromadu z celých čísel (v praxi to budú štruktúry). Binárnu hromadu môžeme jednoducho reprezentovať v jednorozmernom poli celých čísel int x[].
Pre hromadu platí:
- Vrchol hromady – index 1
- Ľubovoľný uzol hromady – x[i]
- Ľavý potomok uzla – x[i*2]
- Pravý potomok uzla – x[i*2+1]
- Index otca vrholu i - [math] \left \lfloor i/2 \right \rfloor[/math]
Reprezentácia hromady pomocou jednorozmerného poľa:
Pri implementácie hromady pomocou jednorozmerného poľa pracujeme od indexu 1!!!
#define MAX_HEAP 100
struct Hromada{
int data[MAX_HEAP];
int n;
};
Opis štruktúry Hromada
- data - jednorozmerné pole prvkov hromady (v našom prípade celých čísel)
- n - aktuálna veľkosť hromady.
Pomocné funkcie pre prácu s hromadou:
- BubbleUp
- Zabezpečí prebublanie ľahkých prvkov smerom hore
- BubbleDown
- Zabezpečí prebublanie ťažkých prvkov smerom dole
Prebublávanie funguje podobne ako pri bublinkovom triedení. Na rozdiel od Bubblesort, prebublávame pozdĺž cesty vedúcej od uzlu v po koreň stromu
Pseudokódy
Poznámka ku pseudokódom: výraz k/2 (n/2) je celočíselné delenie.
1 BubbleUp(k)
2 pokiaľ k>1 a x(k/2)>x(k) rob
3 zamen(k, k/2)
4 k= k/2
5
6 BubbleDown(k)
7 pokiaľ k<=n/2 rob
8 min=2k // inicializacia
9 ak 2k+1 <= n a x(2k)> x(2k+1) tak
10 min=2k+1
11 ak x(min) < x(k) tak
12 zamen(k,min)
13 inak
14 break
15 k=min
16
17 Min
18 return x[1]
19
20 Delete_min
21 x[1]=x[n]
22 n=n-1
23 BubbleDown(n)
24
25 Insert(h)
26 n=n+1
27 x[n]=h
28 BubbleUp(n)
29
30 Delete(k)
31 tmp=x[k]
32 x[k]=x[n]
33 n=n-1
34 ak tmp<=x[k]
35 BubbleDown(k)
36 inak
37 BubbleUp(k)
Vymazanie prvku s minimálnou hodnotou - Delete_min
Vieme, že v hromade je prvok s minimálnou hodnotou vždy na indexe 1. Tento prvok vymažeme a na jeho miesto umiestnime posledný prvok v poli (riadok 21). Tým pádom sa nám zmenší počet prvkov v poli o 1 (riadok 22). Na indexe 1 je prvok z konca poľa. Tento prvok musíme umiestniť na správne miesto pomocou procedúry BubbleDown (riadok 23).
Vloženie nového prvku na hromadu - Insert(n)
Pole zväčšíme o 1 prvok (riadok 26). Do tohoto nového prvku, ktorý je na konci poľa vložíme daný prvok (riadok 27). Tento prvok umiestnime na správen miesto pomocou procedúry BubbleUp (riadok 28)
Vymazanie prvku s na určitim indexe k - Delete
Mažeme prvok na indexe k. Na jeho miesto môžeme umiestniť prvok z konca poľa (riadok 32). Tým sa nám zmenší počet prvkov hromady o 1 (riadok 33). Podľa toho či prvok, ktorý sme vymazali (tmp - riadok 31) bol väčší alebo menší ako poslendý prvok (aktuálne na pozícii k - riadok 34) použijeme procedúru BubbleDown (riadok 35) alebo BubbleUp (riadok 37)
Implementácia v jazyku C
1 #include <iostream.h>
2 #define MAX_HEAP 100
3
4 struct Hromada
5 { int data[ MAX_HEAP];
6 int n;
7 };
8
9 void zamen(Hromada &H,int k, int k2)
10 {
11 int tmp=H.data[k];
12 H.data[k]=H.data[k2];
13 H.data[k2]=tmp;
14 }
15
16 void BubbleUp(Hromada &H, int k)
17 {
18 while(k>1 && H.data[k/2]>H.data[k])
19 {
20 zamen(H,k,k/2);
21 k/=2;
22 }
23 }
24
25 void BubbleDown(Hromada &H, int k)
26 {
27 int min;
28 while(k<= H.n/2) // ak je k potomok lub. uzla
29 {
30 min=2*k; // zitim ktory z dvoch potomkov uzla k je mensi
31 if( (2*k+1)<=H.n && H.data[2*k]>H.data[2*k+1])
32 min=2*k+1;
33 if(H.data[min]<H.data[k]) // prebublavanie dole
34 zamen(H,k,min);
35 else
36 break;
37 k=min;
38 }
39 }
40 void push(Hromada &H, int hodnota)
41 {
42 H.n++;
43 H.data[H.n]=hodnota;
44 BubbleUp(H,H.n);
45 }
46
47 int pop(Hromada &H)
48 {
49 int x=H.data[1];
50 H.data[1]=H.data[H.n];
51 H.n--;
52 BubbleDown(H,1);
53 return x;
54 }
55
56 int Delete(Hromada &H, int k)
57 {
58 int val=H.data[k];
59 H.data[k]=H.data[H.n];
60 H.n--;
61 if( val < H.data[k])
62 BubbleDown(H,k);
63 else
64 BubbleUp(H,k);
65 return val;
66 }
67 void vypis(Hromada H)
68 {
69 for(int i=1;i<=H.n;i++)
70 cout<<H.data[i]<<" ";
71 cout<<endl;
72 }
73 int main()
74 {
75 Hromada heap;
76 heap.n=0;
77 push(heap,10);
78 push(heap,9);
79 push(heap,8);
80 push(heap,7);
81 push(heap,6);
82 push(heap,3);
83
84 vypis(heap);
85
86 int x=pop(heap);
87 cout<<"Vybral som min: "<<x<<endl;
88 vypis(heap);
89
90 cout<<"Mazem prvok s indexom 3: "<<endl;
91 Delete(heap,3);
92 vypis(heap);
93 }