Triedenie výberom: Rozdiel medzi revíziami
| Riadok 90: | Riadok 90: | ||
===Algoritmus Heap Sort=== | ===Algoritmus Heap Sort=== | ||
| − | + | ''Heap Sort'' pri triedení vykonáva dve základné úlohy: Vytvorenie maximálnej binárnej hromady zo vstupného poľa a postupné mazanie jednotlivých prvkov z hromady. Pri oboch procedúrach využíva algoritmus ''Heapify''. | |
====Vlastnosti algoritmu==== | ====Vlastnosti algoritmu==== | ||
| − | * vhodný pre dátové štruktúry: pole | + | * '''vhodný pre dátové štruktúry:''' pole |
| − | * časová náročnosť: vždy linearitmická <math> O(n\log(n)) </math>, vďaka ktorej dokáže efektívne triediť veľmi veľké polia | + | * '''časová náročnosť:''' vždy linearitmická <math> O(n\log(n)) </math>, vďaka ktorej dokáže efektívne triediť veľmi veľké polia |
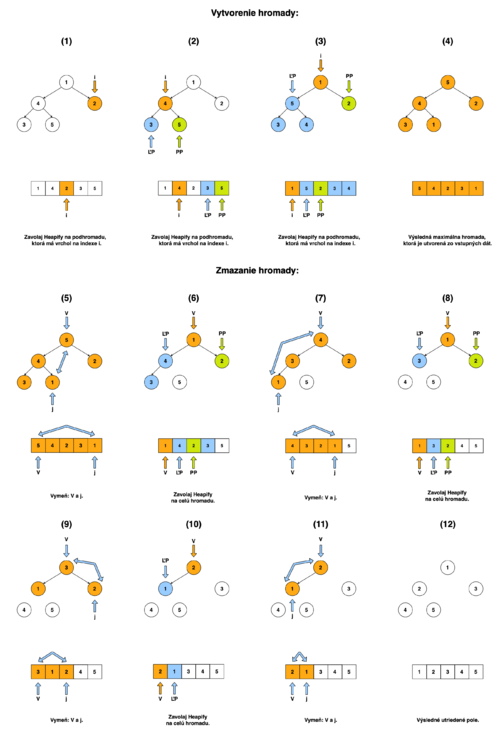
[[Súbor:HeapSort.png|Vizualizácia priebehu algoritmu Heap Sort: Algoritus je znázornený pomocou poľa, ktoré triedime a binárnej hromady, ktorú dané pole reprezentuje. Indexy i a j sú sú iteračné premenné (pozri pseudokód). Indexy ľavého a pravého potomka i-teho prvku sú označené ako ĽP a PP. Vrchol celej hromady je označený ako V. Prvky zafarbené na modro vyjadrujú pravú podhromadu i-teho prvku a prvky zafarbené na zeleno vyjadrujú ľavú pohromadu i-teho prvku. Nevyfarbené prvky vyjadrujú prvky, ktoré boli zmazané. Chronologický priebeh je označený číslicami 1 až 12. |500px|náhľad|vpravo]] | [[Súbor:HeapSort.png|Vizualizácia priebehu algoritmu Heap Sort: Algoritus je znázornený pomocou poľa, ktoré triedime a binárnej hromady, ktorú dané pole reprezentuje. Indexy i a j sú sú iteračné premenné (pozri pseudokód). Indexy ľavého a pravého potomka i-teho prvku sú označené ako ĽP a PP. Vrchol celej hromady je označený ako V. Prvky zafarbené na modro vyjadrujú pravú podhromadu i-teho prvku a prvky zafarbené na zeleno vyjadrujú ľavú pohromadu i-teho prvku. Nevyfarbené prvky vyjadrujú prvky, ktoré boli zmazané. Chronologický priebeh je označený číslicami 1 až 12. |500px|náhľad|vpravo]] | ||
| − | * priestorová náročnosť: konštantná <math>O(1)</math> pri iteračnej verzii, logaritmická <math>O(\log(n))</math> pri rekurzívnej verzii. | + | * '''priestorová náročnosť:''' konštantná <math>O(1)</math> pri iteračnej verzii, logaritmická <math>O(\log(n))</math> pri rekurzívnej verzii. |
| − | * druh triedenia: triedenie výberom (komparačný algoritmus) | + | * '''druh triedenia:''' triedenie výberom (komparačný algoritmus) |
| − | * stabilita triedenia: nestabilný | + | * '''stabilita triedenia:''' nestabilný |
| − | * miesto triedenia: vnútorné triedenie | + | * '''miesto triedenia:''' vnútorné triedenie |
====Základné časti algoritmu==== | ====Základné časti algoritmu==== | ||
| Riadok 109: | Riadok 109: | ||
====Slovný opis==== | ====Slovný opis==== | ||
=====Vytvorenie hromady===== | =====Vytvorenie hromady===== | ||
| − | Pri vytváraní hromady využijeme algoritmus Heapify, pričom hromadu vytvoríme spôsobom zospodu na vrch. | + | Pri vytváraní hromady využijeme algoritmus ''Heapify'', pričom hromadu vytvoríme spôsobom zospodu na vrch. |
| − | Najskôr si určíme rodiča posledného potomka. Využijeme rovnicu (3) z časti | + | Najskôr si určíme rodiča posledného potomka. Využijeme rovnicu (3) z časti "Prehľad", ktorú si jemne upravíme: |
<center><math> \text{posledný rodič:} \ \ i = \left \lfloor \frac{\text{posledný index } - \ 1}{2} \right \rfloor = \left \lfloor\frac{\text{dĺžka } - \ 2}{2} \right \rfloor = \left \lfloor \frac{\text{dĺžka}}{2}\right \rfloor - 1 </math></center> | <center><math> \text{posledný rodič:} \ \ i = \left \lfloor \frac{\text{posledný index } - \ 1}{2} \right \rfloor = \left \lfloor\frac{\text{dĺžka } - \ 2}{2} \right \rfloor = \left \lfloor \frac{\text{dĺžka}}{2}\right \rfloor - 1 </math></center> | ||
| − | Následne zavoláme Heapify na podhromadu s vrcholom na indexe i. Potom postupne zmenšujeme index i o 1 a opakovane naňho voláme Heapify až do chvíle, kým neprídeme na začiatok poľa. Touto procedúrou preusporiadavame spodné jednoprvkové podhromady do 3-prvkových | + | Následne zavoláme ''Heapify'' na podhromadu s vrcholom na indexe ''i''. Potom postupne zmenšujeme index ''i'' o ''1'' a opakovane naňho voláme ''Heapify'' až do chvíle, kým neprídeme na začiatok poľa. Touto procedúrou preusporiadavame spodné jednoprvkové podhromady do 3-prvkových podhromád, tie do 7-prvkových podhromád ... až kým nedostaneme jednu N-prvkovú hromadu, kde ''N'' je počet prvkov v poli. Schematicky by sme to mohli napísať takto: |
<center><math> \text{pre } i \text{ z intervalu } \left \langle \left \lfloor \frac {\text{dĺžka}}{2} \right \rfloor - 1 \quad ; \quad 0 \right \rangle :\ \text{Heapify( pole[], dĺžka, i )}</math></center> | <center><math> \text{pre } i \text{ z intervalu } \left \langle \left \lfloor \frac {\text{dĺžka}}{2} \right \rfloor - 1 \quad ; \quad 0 \right \rangle :\ \text{Heapify( pole[], dĺžka, i )}</math></center> | ||
=====Zmazanie hromady===== | =====Zmazanie hromady===== | ||
| − | Pri mazaní hromady vykonáme dve operácie. Ako prvé vymeníme prvok na vrchu hromady s koncovým prvkom hromady. Prvok čo je na konci poľa považujeme už za zmazaný, preto veľkosť hromady znížime o 1. Ďalej, aby sme splnili podmienky pre maximálnu binárnu hromadu, zavoláme funkciu Heapify na celú hromadu (vrch hromady je 0-tý prvok v poli). Tento proces opakujeme, | + | Pri mazaní hromady vykonáme dve operácie. Ako prvé vymeníme prvok na vrchu hromady s koncovým prvkom hromady. Prvok čo je na konci poľa považujeme už za zmazaný, preto veľkosť hromady znížime o 1. Ďalej, aby sme splnili podmienky pre maximálnu binárnu hromadu, zavoláme funkciu ''Heapify'' na celú hromadu (vrch hromady je 0-tý prvok v poli). Tento proces opakujeme, pokým v hromade neostanú žiadne prvky. |
Poznámka: Pri triediacom algoritme nemusíme mazať celú hromadu, stačí nám, keď v hromade ostane jeden prvok, pretože vtedy bude vstupné pole už utriedené. | Poznámka: Pri triediacom algoritme nemusíme mazať celú hromadu, stačí nám, keď v hromade ostane jeden prvok, pretože vtedy bude vstupné pole už utriedené. | ||
| Riadok 124: | Riadok 124: | ||
<center><math>\text{pre } j \text{ z intervalu } \left \langle \text{dĺžka - 1} \quad ; \quad 0 \right ) : \ \ \text{Vymeň(pole[0], pole[$j$])} \ \ a \ \ \text{Heapify(pole[], dĺžka, 0)} </math></center> | <center><math>\text{pre } j \text{ z intervalu } \left \langle \text{dĺžka - 1} \quad ; \quad 0 \right ) : \ \ \text{Vymeň(pole[0], pole[$j$])} \ \ a \ \ \text{Heapify(pole[], dĺžka, 0)} </math></center> | ||
| − | Z hľadiska implementácie môžeme vytvoriť rekurzívnu | + | Z hľadiska implementácie môžeme vytvoriť '''iteračnú''' aj '''rekurzívnu''' verziu, čo závisí len od toho, ako je implementovaná funkcia ''Heapify''. |
====Pseudokód==== | ====Pseudokód==== | ||
| − | Nech funkcia Heap Sort má nasledovný prototyp: <code>HeapSort(pole[], dlzka)</code> | + | Nech funkcia ''Heap Sort'' má nasledovný prototyp: <code>HeapSort(pole[], dlzka)</code> |
:1. Nech: <code>i = dlzka / 2 - 1</code>, kde "/" predstavuje celočíslené delenie. | :1. Nech: <code>i = dlzka / 2 - 1</code>, kde "/" predstavuje celočíslené delenie. | ||
Verzia zo dňa a času 16:51, 19. apríl 2021
Obsah
Heap Sort
Prehľad
Heap Sort je triediaci algoritmus, ktorý podobne ako Selection sort, rozeľuje pole na zotriedenú a nezotriedenú časť, pričom nezotriedená časť predstavuje dátovú štruktúru binárna hromada. Celé triedenie spočíva v tom, že si zo vstupného poľa vytvoríme binárnu hromadu a následne postupným vyberaním a mazaním všetkých jej prvkov toto pole utriedime.
Hromada, ktorú využíva algoritmus Heap Sort, musí spĺňať nasledovné podmienky (ak indexujeme pole od 0):
- 1. Vrchol hromady (koreň) je vždy prvý prvok v poli (v našom prípade prvok na 0-tej pozícii).
- 2. Pre ľubovoľný prvok (uzol), uložený na indexe [math]i[/math] z intervalu [math] \langle 0 \ ; \ \text{dĺžka} - 1 \rangle [/math], platia nasledovné rovnice:
- [math] \begin{align} \text{ľavý potomok} &= 2i + 1 && (1) \\ \text{pravý potomok} &= 2i + 2 && (2) \\ \text{rodič} &= \left \lfloor \frac{i - 1}{2} \right \rfloor \quad (\text {okrem} \ i = 0) && (3) \end{align} [/math]
- 3. Každý prvok (uzol) v hromade musí mať väčšiu, alebo rovnakú hodnotu ako jeho potomkovia (vlastnosť MAX HEAP - ak triedime pole vzostupne, v opačnom prípade by sme použili MIN HEAP).
Algoritmus Heapify
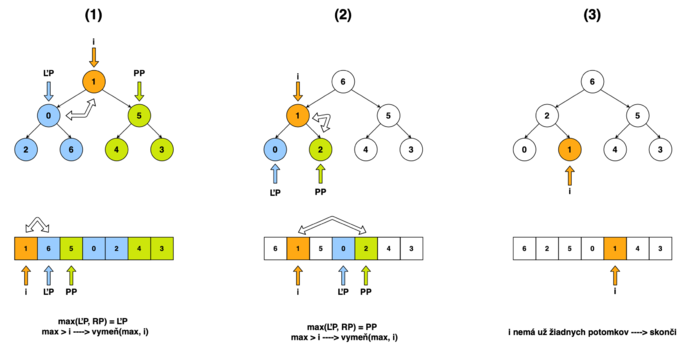
Heapify je kľúčovým podprogramom triediaceho algoritmu Heap Sort, vďaka ktorému vieme efektíve zabezpečiť procedúry: vytvorenie hromady z poľa a zmazanie hromady.
Princíp algoritmu Heapify spočíva v tom, že ak máme i-ty prvok v poli (v kompletnom binárnom strome), ktorého potomkovia tvoria dve samostatné podhromady, potom tieto dve podhromady preusporiadame do jednej hromady, pričom i-ty prvok bude jej vrcholom.
Vlastnosti algoritmu
- dátová štruktúra: hromada (reprezentovaná ako: pole)
- časová zložitosť: lineárna [math]O(n)[/math]
- priestorová zložitosť: konštantná [math]O(1)[/math] pri iteračnej verzii, [math]O(log(n))[/math] pri rekurzívnej verzii
Základné časti algoritmu
- Určenie potomka i-teho prvku s maximálnou hodnotou.
- Porovnanie hodnoty maximálneho potomka s hodnotou rodiča (i-tym prvkom).
- Ak je hodnota maximálneho potomka väčšia ako hodnota rodiča, tak výmena potomka a rodiča.
- Ak nastane výmena, skontrolovanie ovplyvneného potomka (podhromady).
Slovný opis algoritmu
Na vstupe prijmeme pole a index i, v ktorom chceme vytvoriť hromadu (Max Heap). Musí byť splnená podmienka, že oba potomkovia i-teho prvku tvoria dve samostatné podhromady. Najskôr skontrolujeme, či prvok na indexe i má nejakých potomkov (využijeme rovnice (1) a (2) z časti "Prehľad"). Ak nemá žiadnych potomkov, funkcia skončí, pretože i predstavuje vrchol jednoprvkovej hromady. Ak má práve jedného potomka, tento potomok je zároveň aj jeho maximálnym potomkom. Ak má práve dvoch potomkov, tak porovnáme ich hodnoty a vyberieme z nich maximálneho potomka. Následne skontrolujeme veľkosť maximálneho potomka a jeho rodiča (prvok na indexe i). Ak je rodič väčší, funkcia skončí, pretože želaná hromada už je utvorená. Ak nie, vymeníme rodiča a maximálneho potomka. Ak nastala výmena, musíme skontrolovať ovplyvnenú podhromadu, tj. zopakovať tento sled krokov pre podhromadu, ktorej vrchol bude v maximálnom potomkovi i-teho prvku.
Z hľadiska implementácie môžeme vytvoriť iteračnú aj rekurzívnu verziu.
Pseudokód
Nech funkcia Heapify má nasledovný prototyp: Heapify(pole[], dlzka, i)
- 1. Je
2 * i + 1 < dlzka? Ak áno, pokračuj krokom 1.1., inak skonči.- 1.1. Nech:
lavy = 2 * i + 1 - 1.2. Nech:
pravy = 2 * i + 2 - 1.3. Je
pravy < dlzkaa zároveňpole[pravy] > pole[lavy]?- Ak áno:
- 1.3.1. Nech:
max = pravy
- 1.3.1. Nech:
- Ak nie:
- 1.3.1. Nech:
max = lavy
- 1.3.1. Nech:
- Ak áno:
- 1.4. Je
pole[max] > pole[i]?- Ak áno:
- 1.4.1. Vymeň:
pole[max]apole[i] - 1.4.2.
i = max
- 1.4.1. Vymeň:
- Ak nie:
- 1.4.1 Skonči.
- Ak áno:
- 1.5. Skoč na krok 1.
- 1.1. Nech:
Nech funkcia Heapify má nasledovný prototyp: Heapify(pole[], dlzka, i)
- 1. Nech:
lavy = 2 * i + 1 - 2. Nech:
pravy = 2 * i + 2 - 3. Nech:
max = i - 4. Je
lavy < dlzkaa zároveňpole[lavy] > pole[i]?- Ak áno:
- 4.1. Nech:
max = lavy
- 4.1. Nech:
- Ak nie:
- 4.1. Pokračuj krokom 5.
- Ak áno:
- 5. Je
pravy < dlzkaa zároveňpole[pravy] > pole[i]?- Ak áno:
- 5.1. Nech:
max = pravy
- 5.1. Nech:
- Ak nie:
- 5.1. Pokračuj krokom 6.
- Ak áno:
- 6. Je
pole[max] > pole[i]?- Ak áno:
- 6.1. Vymeň:
pole[i] a pole[max] - 6.2. Rekurzívne zavolaj:
Heapify(pole[], dlzka, max)
- 6.1. Vymeň:
- Ak nie:
- 6.1. Skonči volanie.
- Ak áno:
Algoritmus Heap Sort
Heap Sort pri triedení vykonáva dve základné úlohy: Vytvorenie maximálnej binárnej hromady zo vstupného poľa a postupné mazanie jednotlivých prvkov z hromady. Pri oboch procedúrach využíva algoritmus Heapify.
Vlastnosti algoritmu
- vhodný pre dátové štruktúry: pole
- časová náročnosť: vždy linearitmická [math] O(n\log(n)) [/math], vďaka ktorej dokáže efektívne triediť veľmi veľké polia
- priestorová náročnosť: konštantná [math]O(1)[/math] pri iteračnej verzii, logaritmická [math]O(\log(n))[/math] pri rekurzívnej verzii.
- druh triedenia: triedenie výberom (komparačný algoritmus)
- stabilita triedenia: nestabilný
- miesto triedenia: vnútorné triedenie
Základné časti algoritmu
- Vytvorenie binárnej hromady z poľa.
- Zmazanie binárnej hromady.
Slovný opis
Vytvorenie hromady
Pri vytváraní hromady využijeme algoritmus Heapify, pričom hromadu vytvoríme spôsobom zospodu na vrch.
Najskôr si určíme rodiča posledného potomka. Využijeme rovnicu (3) z časti "Prehľad", ktorú si jemne upravíme:
Následne zavoláme Heapify na podhromadu s vrcholom na indexe i. Potom postupne zmenšujeme index i o 1 a opakovane naňho voláme Heapify až do chvíle, kým neprídeme na začiatok poľa. Touto procedúrou preusporiadavame spodné jednoprvkové podhromady do 3-prvkových podhromád, tie do 7-prvkových podhromád ... až kým nedostaneme jednu N-prvkovú hromadu, kde N je počet prvkov v poli. Schematicky by sme to mohli napísať takto:
Zmazanie hromady
Pri mazaní hromady vykonáme dve operácie. Ako prvé vymeníme prvok na vrchu hromady s koncovým prvkom hromady. Prvok čo je na konci poľa považujeme už za zmazaný, preto veľkosť hromady znížime o 1. Ďalej, aby sme splnili podmienky pre maximálnu binárnu hromadu, zavoláme funkciu Heapify na celú hromadu (vrch hromady je 0-tý prvok v poli). Tento proces opakujeme, pokým v hromade neostanú žiadne prvky.
Poznámka: Pri triediacom algoritme nemusíme mazať celú hromadu, stačí nám, keď v hromade ostane jeden prvok, pretože vtedy bude vstupné pole už utriedené.
Schematicky by sme to mohli zapísať takto:
Z hľadiska implementácie môžeme vytvoriť iteračnú aj rekurzívnu verziu, čo závisí len od toho, ako je implementovaná funkcia Heapify.
Pseudokód
Nech funkcia Heap Sort má nasledovný prototyp: HeapSort(pole[], dlzka)
- 1. Nech:
i = dlzka / 2 - 1, kde "/" predstavuje celočíslené delenie. - 2. Je
i >= 0? Ak áno, pokračuj krokom 2.1., inak skoč na krok 3.- 2.1. Zavolaj funkciu:
Heapify(pole[], dlzka, i) - 2.2.
i = i - 1 - 2.3. Skoč na krok 2.
- 2.1. Zavolaj funkciu:
- 3. Nech:
j = dlzka - 1 - 4 Je
j > 0? Ak áno, pokračuj krokom 4.1, inak skonči.- 4.1. Vymeň:
pole[0]apole[j] - 4.2. Zavolaj funkciu:
Heapify(pole[], j, 0) - 4.3.
j = j - 1 - 4.4. Skoč na krok 4.
- 4.1. Vymeň:
Implementácia algoritmov Heapify a HeapSort v rôznych programovacích jazykoch
#include <stdio.h>
void Vymen(int *a, int *b);
void Heapify(int pole[], int dlzka, int index);
void HeapSort(int pole[], int dlzka);
int main()
{
int pole[]= {10, 5, 2, 9, 8, 7, 1, 3, 4, 0, -1};
int dlzka = sizeof(pole) / sizeof(pole[0]);
HeapSort(pole, dlzka);
for (int i = 0; i < dlzka; ++i)
{
printf("%d ", pole[i]);
}
}
void Vymen(int *a, int *b)
{
int tmp = *a;
*a = *b;
*b = tmp;
}
void Heapify(int pole[], int dlzka, int index)
{
int pravy, lavy, max;
while(2 * index + 1 < dlzka)
{
lavy = 2 * index + 1;
pravy = 2 * index + 2;
// určenie potomka s maximálnou hodnotou
if(pravy < dlzka && pole[pravy] > pole[lavy])
{
max = pravy;
}
else
{
max = lavy;
}
// porovnanie maximálneho potomka s rodičom
if(pole[max] > pole[index])
{
Vymen(&pole[max], &pole[index]);
index = max;
}
else
{
return;
}
}
}
void HeapSort(int pole[], int dlzka)
{
// vytvor maximálnu hromadu (procedúra BuildMaxHeap)
for (int i = dlzka / 2 - 1 ; i >= 0; --i)
{
Heapify(pole, dlzka, i);
}
// zmaž všetky prvky z hromady
for (int j = dlzka - 1; j > 0; --j)
{
Vymen(&pole[0], &pole[j]);
Heapify(pole, j, 0);
}
}
#include <stdio.h>
void Vymen(int *a, int *b);
void Heapify(int pole[], int dlzka, int index);
void HeapSort(int pole[], int dlzka);
int main()
{
int pole[]= {10, 5, 2, 9, 8, 7, 1, 3, 4, 0, -1, -1};
int dlzka = sizeof(pole) / sizeof(pole[0]);
HeapSort(pole, dlzka);
for (int i = 0; i < dlzka; ++i)
{
printf("%d ", pole[i]);
}
}
void Vymen(int *a, int *b)
{
int tmp = *a;
*a = *b;
*b = tmp;
}
void Heapify(int pole[], int dlzka, int index)
{
int lavy = 2 * index + 1;
int pravy = 2 * index + 2;
int max = index;
// určenie potomka s maximálnou hodnotou
if(lavy < dlzka && pole[lavy] >= pole[pravy])
{
max = lavy;
}
if(pravy < dlzka && pole[pravy] > pole[lavy])
{
max = pravy;
}
// porovnanie maximálneho potomka s rodičom
if(pole[max] > pole[index])
{
Vymen(&pole[max], &pole[index]);
Heapify(pole, dlzka, max);
}
}
void HeapSort(int pole[], int dlzka)
{
// vytvor maximálnu hromadu (procedúra BuildMaxHeap)
for (int i = dlzka / 2 - 1 ; i >= 0; --i)
{
Heapify(pole, dlzka, i);
}
// zmaž všetky prvky z hromady
for (int j = dlzka - 1; j > 0; --j)
{
Vymen(&pole[0], &pole[j]);
Heapify(pole, j, 0);
}
}
class HeapSortIT {
void swap(int[] pole, int a, int b) {
int tmp = pole[a];
pole[a] = pole[b];
pole[b] = tmp;
}
void heapify(int[] pole, int n) {
for (int i = 1; i < n; i++) {
/* Ak je potomok väčší ako rodič */
if (pole[i] > pole[(i - 1) / 2]) {
int j = i;
/* Vymieňaj elementy (rodič, potomok), dokým je rodič menší ako potomok */
while (pole[j] > pole[(j - 1) / 2]) {
swap(pole, j, (j - 1) / 2);
j = (j - 1) / 2;
}
}
}
}
void sort(int[] pole) {
int n = pole.length;
heapify(pole, n);
for (int i = n - 1; i > 0; i--) {
int j = 0, index;
/* Vymeň prvý a posledný prvok */
swap(pole, 0, i);
do {
index = 2 * j + 1;
/* Ak je ľavý potomok menši ako pravý, presuň 'index' na pravého potomka */
if (index < i - 1 && pole[index] < pole[index + 1])
index++;
/* Ak je rodič menší ako potomok, tak ho vymeň s potomkom, ktorý má väčšiu hodnotu */
if (index < i && pole[j] < pole[index])
swap(pole, j, index);
j = index;
} while (index < i);
}
}
}
public class Main {
static void printArray(int[] pole) {
int n = pole.length;
for (int i : pole)
System.out.print(i + " ");
System.out.println();
}
public static void main(String[] args) {
int[] pole = {12, 11, 13, 5, 6, 7};
int n = pole.length;
System.out.println("Pole pred zoradenim: ");
printArray(pole);
HeapSortIT hs = new HeapSortIT();
hs.sort(pole);
System.out.println("Pole po zoradeni: ");
printArray(pole);
}
}
class HeapSortRE {
void swap(int[] pole, int a, int b) {
int tmp = pole[a];
pole[a] = pole[b];
pole[b] = tmp;
}
void heapify(int[] pole, int n, int i) {
int max = i; // rodič
int l = 2 * i + 1; // ľavý potomok
int p = 2 * i + 2; // pravý potomok
/* Ak je ľavý potomok väčší ako rodič */
if (l < n && pole[l] > pole[max])
max = l;
/* Ak je pravý potomok väčší ako rodič */
if (p < n && pole[p] > pole[max])
max = p;
/* Ak sa rodič v priebehu funkcie zmenil */
if (max != i) {
swap(pole, i, max);
heapify(pole, n, max);
}
}
public void sort(int[] pole) {
int n = pole.length;
/* Vytvorenie hromadu */
for (int i = n / 2 - 1; i >= 0 ; i--)
heapify(pole, n, i);
/* Extrahovanie jednotlivých elemetov z hromady */
for (int i = n - 1; i > 0; i--) {
/* Presuň aktuálneho rodiča na koniec */
swap(pole, 0, i);
/* Zavolanie heapify na zredukovanú hromadu */
heapify(pole, i, 0);
}
}
}
public class Main {
static void printArray(int[] pole) {
int n = pole.length;
for (int i : pole)
System.out.print(i + " ");
System.out.println();
}
public static void main(String[] args) {
int[] pole = {12, 11, 13, 5, 6, 7};
int n = pole.length;
System.out.println("Pole pred zoradenim: ");
printArray(pole);
HeapSortRE hs = new HeapSortRE();
hs.sort(pole);
System.out.println("Pole po zoradeni: ");
printArray(pole);
}
}
def heapify(pole, n):
for i in range(n):
# Ak je potomok väčší ako rodič
if pole[i] > pole[int((i - 1) / 2)]:
j = i
# Vymieňaj elementy (rodič, potomok), dokým je rodič menší ako potomok
while pole[j] > pole[int((j - 1) / 2)]:
pole[j], pole[int((j - 1) / 2)] = pole[int((j - 1) / 2)], pole[j] # swap
j = int((j - 1) / 2)
def sort(pole, n):
heapify(pole, n)
for i in range(n - 1, 0, -1):
# Vymeň prvý a posledný prvok
pole[0], pole[i] = pole[i], pole[0] # swap
j, index = 0, 0
while True:
index = 2 * j + 1
# Ak je ľavý potomok menši ako pravý, presuň 'index' na pravého potomka
if index < (i - 1) and pole[index] < pole[index + 1]:
index += 1
# Ak je rodič menší ako potomok, tak ho vymeň s potomkom, ktorý má väčšiu hodnotu
if index < i and pole[j] < pole[index]:
pole[j], pole[index] = pole[index], pole[j] # swap
j = index
if index >= i:
break
def printArray(pole, n):
for i in range(n):
print(pole[i], end=" ")
if __name__ == '__main__':
pole = [12, 11, 13, 5, 6, 7]
n = len(pole)
print("Zadane pole:")
printArray(pole, n)
sort(pole, n)
print("\nZoradene pole:")
printArray(pole, n)
def heapify(pole, n, i):
max = i # rodic
l = 2 * i + 1 # lavy potomok
p = 2 * i + 2 # pravy potomok
# Ak je ľavý potomok väčší ako rodič
if l < n and pole[max] < pole[l]:
max = l
# Ak je pravý potomok väčší ako rodič
if p < n and pole[max] < pole[p]:
max = p
# Ak sa rodič v priebehu funkcie zmenil
if max != i:
pole[i], pole[max] = pole[max], pole[i] # swap
heapify(pole, n, max)
def sort(pole):
n = len(pole)
# Vytvorenie hromady
for i in range(n // 2 - 1, -1, -1):
heapify(pole, n, i)
# Extrahovanie jednotlivých elementov z hromady
for i in range(n - 1, 0, -1):
pole[i], pole[0] = pole[0], pole[i] # swap
heapify(pole, i, 0)
def printArray(pole):
n = len(pole)
for i in range(n):
print(pole[i], end=" ")
if __name__ == '__main__':
pole = [12, 11, 13, 5, 6, 7]
print("Zadane pole:")
printArray(pole)
sort(pole)
print("\nZoradene pole:")
printArray(pole)
Selection Sort
Prehľad
Selection Sort je triediaci algoritmus, ktorý si rozdelí pole na dve časti: zotriedenú a nezotriedenú. Následne opakovane vyberá minimum v nezotriedenej časti (ak triedime vzostupne), ktoré umiestni na koniec utrienej časti.
Vlastnosti algoritmu
- vhodný pre dátové štruktúry: pole
- časová náročnosť: vždy kvadratická [math] O(n^2) [/math], čo znamená, že algoritmus je určený na triedenie veľmi malých polí (rádovo 10, 20 prvkov), vďaka minimálnej réžii a jednoduchej implementácii, avšak pre väčšie polia sa stáva veľmi neefektívny
- priestorová náročnosť: vždy konštantná [math]O(1)[/math]
- druh triedenia: triedenie výberom (komparačný algoritmus)
- stabilita triedenia: nestabilný
- miesto triedenia: vnútorné triedenie
Základné časti algoritmu
- Vonkajší cyklus: nastavenie hornej hranice utriedenej časti.
- Vnútorný cyklus: hľadanie minima ....
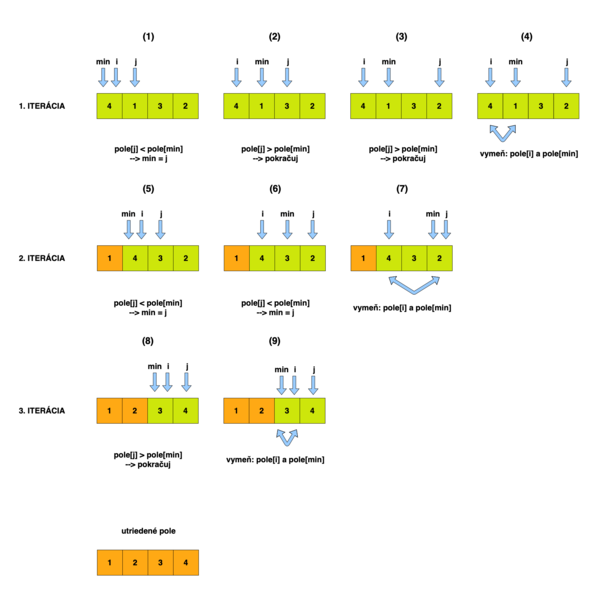
Slovný opis algoritmu
Pseudokód
Nech má funkcia Selection Sort nasledovný prototyp: SelectionSort(pole[], dlzka)
- 1. Nech:
min = pole[0] - 2. Nech
i = 1 - 3. Je
i < dlzka? Ak áno, pokračuj krokom 3.1., inak skonči.- 3.1. Nech:
j = i - 3.2. Je
j < dlzka? Ak áno, pokračuj krokom 3.2.1. , inak skoč na krok 3.3.- 3.2.1. Je
pole[j] < min?- Ak áno:
- 3.2.1.1.
min = pole[j] - 3.2.1.2. Skoč na krok 3.2.
- 3.2.1.1.
- Ak nie:
- 3.2.1.1. Skoč na krok 3.2.
- Ak áno:
- 3.2.1. Je
- 3.3. Vymeň:
pole[i]apole[min] - 3.4. Skoč na krok 3.2.
- 3.1. Nech:
Odkazy
Heap Sort:
https://en.wikipedia.org/wiki/Heapsort
https://www.geeksforgeeks.org/heap-sort/