Triedenie výberom: Rozdiel medzi revíziami
Skočit na navigaci
Skočit na vyhledávání
| Riadok 4: | Riadok 4: | ||
__TOC__ | __TOC__ | ||
==Tento článok je v prvotnom štádiu konštrukcie, zatiaľ je to len hromada myšlienok :)== | ==Tento článok je v prvotnom štádiu konštrukcie, zatiaľ je to len hromada myšlienok :)== | ||
| − | |||
| − | |||
| − | + | ==Heap Sort== | |
| − | + | Algoritmus Heap Sort na triedenie využíva dátovú štruktúru [[Hromada|binárna hromada]], ktorú si vytvorí zo vstupného poľa, ktoré máme utriediť a následne zmazaním všetkých jej prvkov dosiahneme utriedené pole. | |
| − | + | ||
| + | Hromada, ktorú vytvoríme musí spĺňať nasledovné podmienky: | ||
| + | :1. Vrchol hromady je vždy prvý prvok v poli (v našom prípade prvok na 0-tej pozícii). | ||
| + | :2. Pre ľubovoľný prvok uložený na indexe <math>i</math> z intervalu <math> \langle 0 \ ; \ \text{dĺžka} - 1 \rangle </math> platia nasledovné rovnice: | ||
:: <math> | :: <math> | ||
\begin{align} | \begin{align} | ||
| Riadok 16: | Riadok 17: | ||
\text{rodič} &= \left \lfloor \frac{i - 1}{2} \right \rfloor \quad (\text {okrem} \ i = 0) && (3) | \text{rodič} &= \left \lfloor \frac{i - 1}{2} \right \rfloor \quad (\text {okrem} \ i = 0) && (3) | ||
\end{align} | \end{align} | ||
| − | </math> | + | </math> |
| + | :3. Každý prvok (uzol) v hromade musí mať väčšiu, alebo rovnakú hodnotu ako jeho potomkovia (MAX HEAP - ak triedime pole od vzostupne). | ||
| − | + | ===Algoritmus Heapify=== | |
| − | + | [[Súbor:Heapify.png|1045px|náhľad|vpravo]] | |
| − | ==Algoritmus Heapify== | + | Heapify je kľúčovým podprogramom triediaceho algoritmu Heap Sort. |
| − | |||
| − | |||
| − | ===Základné časti algoritmu=== | + | ====Základné časti algoritmu==== |
# Určenie maxima z 2 potomkov i-teho prvku a porovnanie s veľkosťou rodiča. | # Určenie maxima z 2 potomkov i-teho prvku a porovnanie s veľkosťou rodiča. | ||
# Ak je potomok väčší ako rodič, tak výmena potomka a rodiča. | # Ak je potomok väčší ako rodič, tak výmena potomka a rodiča. | ||
# Skontrolovanie ovplyvneného potomka (podstromu). | # Skontrolovanie ovplyvneného potomka (podstromu). | ||
| − | ===Slovný opis algoritmu=== | + | ====Slovný opis algoritmu==== |
| + | Ak máme i-ty prvok v poli, pričom oba jeho potomkovia tvoria dve samostatné podhromady, potom funkcia Heapify zlúči tieto dve podhromady do jednej hromady, pričom i-ty prvok bude jej vrcholom. | ||
| − | ===Vlastnosti algoritmu=== | + | ====Vlastnosti algoritmu==== |
* dátová štruktúra: hromada (pole) | * dátová štruktúra: hromada (pole) | ||
* časová zložitosť: lineárna <math>O(n)</math> | * časová zložitosť: lineárna <math>O(n)</math> | ||
| Riadok 37: | Riadok 38: | ||
| − | |||
| − | |||
| − | |||
==Selection Sort== | ==Selection Sort== | ||
Verzia zo dňa a času 18:30, 3. apríl 2021
Obsah
Tento článok je v prvotnom štádiu konštrukcie, zatiaľ je to len hromada myšlienok :)
Heap Sort
Algoritmus Heap Sort na triedenie využíva dátovú štruktúru binárna hromada, ktorú si vytvorí zo vstupného poľa, ktoré máme utriediť a následne zmazaním všetkých jej prvkov dosiahneme utriedené pole.
Hromada, ktorú vytvoríme musí spĺňať nasledovné podmienky:
- 1. Vrchol hromady je vždy prvý prvok v poli (v našom prípade prvok na 0-tej pozícii).
- 2. Pre ľubovoľný prvok uložený na indexe [math]i[/math] z intervalu [math] \langle 0 \ ; \ \text{dĺžka} - 1 \rangle [/math] platia nasledovné rovnice:
- [math] \begin{align} \text{ľavý potomok} &= 2i + 1 && (1) \\ \text{pravý potomok} &= 2i + 2 && (2) \\ \text{rodič} &= \left \lfloor \frac{i - 1}{2} \right \rfloor \quad (\text {okrem} \ i = 0) && (3) \end{align} [/math]
- 3. Každý prvok (uzol) v hromade musí mať väčšiu, alebo rovnakú hodnotu ako jeho potomkovia (MAX HEAP - ak triedime pole od vzostupne).
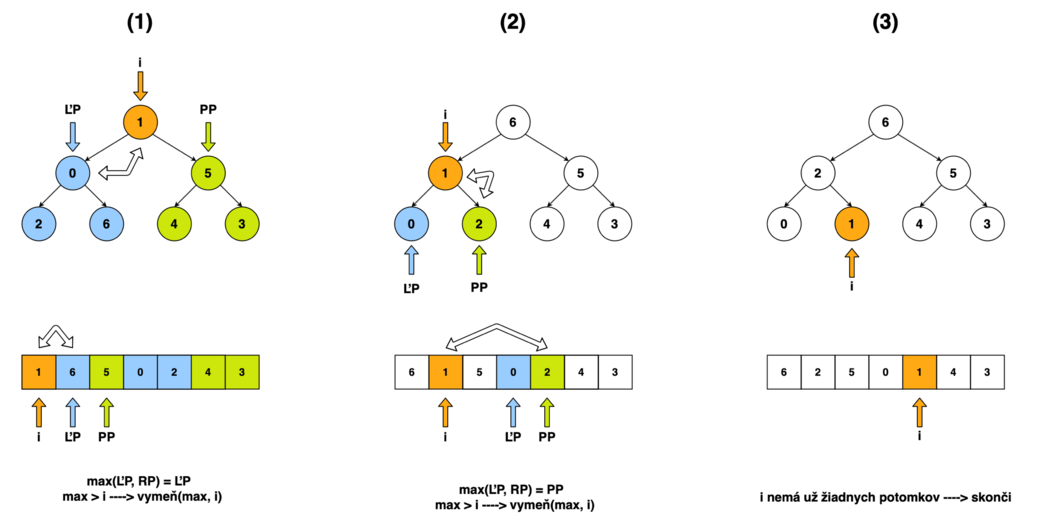
Algoritmus Heapify
Heapify je kľúčovým podprogramom triediaceho algoritmu Heap Sort.
Základné časti algoritmu
- Určenie maxima z 2 potomkov i-teho prvku a porovnanie s veľkosťou rodiča.
- Ak je potomok väčší ako rodič, tak výmena potomka a rodiča.
- Skontrolovanie ovplyvneného potomka (podstromu).
Slovný opis algoritmu
Ak máme i-ty prvok v poli, pričom oba jeho potomkovia tvoria dve samostatné podhromady, potom funkcia Heapify zlúči tieto dve podhromady do jednej hromady, pričom i-ty prvok bude jej vrcholom.
Vlastnosti algoritmu
- dátová štruktúra: hromada (pole)
- časová zložitosť: lineárna [math]O(n)[/math]
- priestorová zložitosť: konštantná [math]O(1)[/math] pri iteračnej verzii, [math]O(log(N))[/math] pri rekurzívnej verzii