Triedenie výberom: Rozdiel medzi revíziami
Skočit na navigaci
Skočit na vyhledávání
| Riadok 35: | Riadok 35: | ||
* časová zložitosť: lineárna <math>O(n)</math> | * časová zložitosť: lineárna <math>O(n)</math> | ||
* priestorová zložitosť: konštantná <math>O(1)</math> pri iteračnej verzii, <math>O(log(N))</math> pri rekurzívnej verzii | * priestorová zložitosť: konštantná <math>O(1)</math> pri iteračnej verzii, <math>O(log(N))</math> pri rekurzívnej verzii | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Verzia zo dňa a času 17:40, 3. apríl 2021
Obsah
Tento článok je v prvotnom štádiu konštrukcie, zatiaľ je to len hromada myšlienok :)
Zlučovací algoritmus Heapify
Algoritmus Heapify predstavuje kľúčový podprogram pre triediaci algoritmus Heap sort. pracuje s dátovou štruktúrou binárna hromada
Všeobecne platí, že každý kompletný binárny strom môžeme byť vyjadrený pomocou poľa s využitím nasledovných zákonitostí:
- Koreň stromu je vždy prvý prvok v poli (v našom prípade prvok na 0-tej pozícii).
- Pre ľubovoľný index [math]i[/math] z intervalu [math] \langle 0 \ ; \ \text{dĺžka} - 1 \rangle [/math] platia nasledovné rovnice:
- [math] \begin{align} \text{ľavý potomok} &= 2i + 1 && (1) \\ \text{pravý potomok} &= 2i + 2 && (2) \\ \text{rodič} &= \left \lfloor \frac{i - 1}{2} \right \rfloor \quad (\text {okrem} \ i = 0) && (3) \end{align} [/math]
Na základe týchto zákonitostí môžeme vytvoriť algoritmus Heapify, vďaka ktorému vieme elegantne uskutočniť operácie s hromadou, ako je vytvorenie hromady z poľa, zmazanie jednotlivých prvkov z hromady, čo sú základné časti triediaceho algoritmu Heap Sort.
Algoritmus Heapify
Ak máme i-ty prvok v poli, pričom oba jeho potomkovia tvoria dve samostatné hromady, potom funkcia Heapify zlúči tieto dve hromady do jednej, pričom i-ty prvok bude jej koreňom.
Základné časti algoritmu
- Určenie maxima z 2 potomkov i-teho prvku a porovnanie s veľkosťou rodiča.
- Ak je potomok väčší ako rodič, tak výmena potomka a rodiča.
- Skontrolovanie ovplyvneného potomka (podstromu).
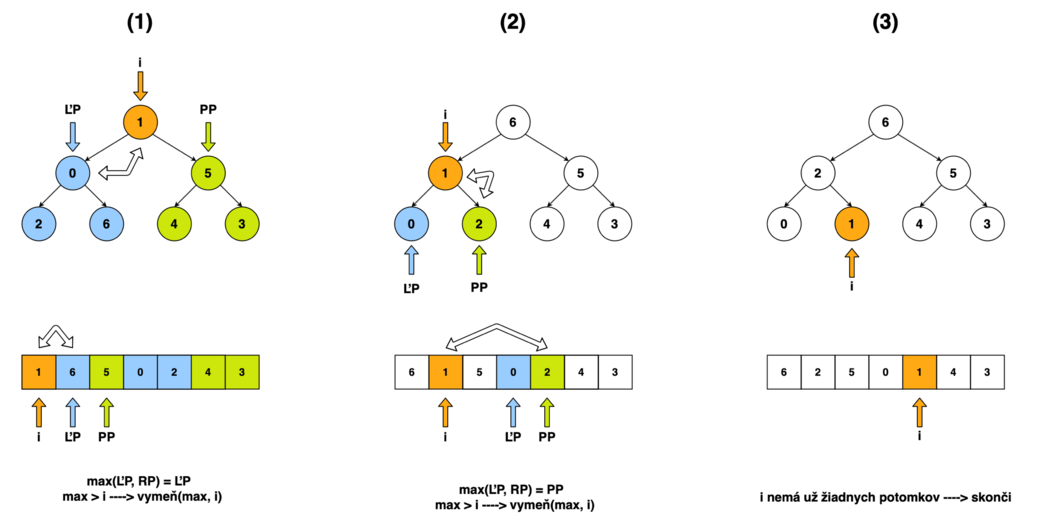
Slovný opis algoritmu
Vlastnosti algoritmu
- dátová štruktúra: hromada (pole)
- časová zložitosť: lineárna [math]O(n)[/math]
- priestorová zložitosť: konštantná [math]O(1)[/math] pri iteračnej verzii, [math]O(log(N))[/math] pri rekurzívnej verzii