Triedenie zlučovaním

Algoritmy a programovanie

---

Dátový typ

Štruktúry

Rekurzia

Algoritmy vyhľadávania

Algoritmy triedenia

>Triedenie výmenou
>Triedenie vkladaním
>Triedenie zlučovaním
>Triedenie delením
>Triedenie výberom
>Triedenie - ostatné princípy

Lineárny zoznam

Binárny strom

Numerické algoritmy

Grafové algoritmy

Merge sort

Merge Sort je triediaci algoritmus, ktorý je založený na princípe "rozdeľ a panuj", čo znamená, že pole najskôr rozdelí na dve polovice, tie zoradí a potom ich zlúči naspäť dokopy. Keďže najhoršia doba výpočtu je [math]O(n.log(n))[/math], tak sa radí medzi najpoužívanejšie a najviac rešpektované triediacie algoritmy.

Princíp algoritmu

Pri algoritme Mergesort využívame stratégiu "rozdeľuj a panuj", čo znamená, že celé pole s veľkosťou n prvkov si rozdelíme na na 2 menšie polia (ako pri binárnom vyhľadávaní) a ...

Zlučovacia funkcia "Merge":

Princíp zlučovania

Vo všeobecnosti princíp zlučovania tkvie v tom, že zoberieme dva (alebo viac) menšie utriedné zoznamy, ktoré skombinujeme do jedného väčšieho utriedeného zoznamu. Zoznam môže byť reprezentovaný ako dátová štruktúra pole alebo aj ako lineárny zoznam. V tejto časti sa zameriame na algoritmus pre dátovú štruktúru pole.

Slovný opis alogritmu

Pri funkcii Merge využívame princíp zlučovania tak, že máme pole, ktoré sa skladá z dvoch už utriedených polovíc. Následne si vytvoríme dve pomocné polia, do ktorých skopíruje obsahy oboch polovíc. Potom súčasne prechádzame obe pomocné polia a vždy z uvažovanej dvojice prvkov vyberáme ten menší z nich (keď triedime od najväčšieho po najmenší) a vložíme ho na začiatok pôvodného poľa. Index zvýšime iba pri tom poli z ktorého sme daný prvok vybrali. Ak nastane situácia, že z jedného pomocného poľa vyberieme všetky prvky skôr, ako z druhého pomocného poľa, potom zbytok druhého pomocného poľa už iba kopírujeme na koniec pôvodného poľa.

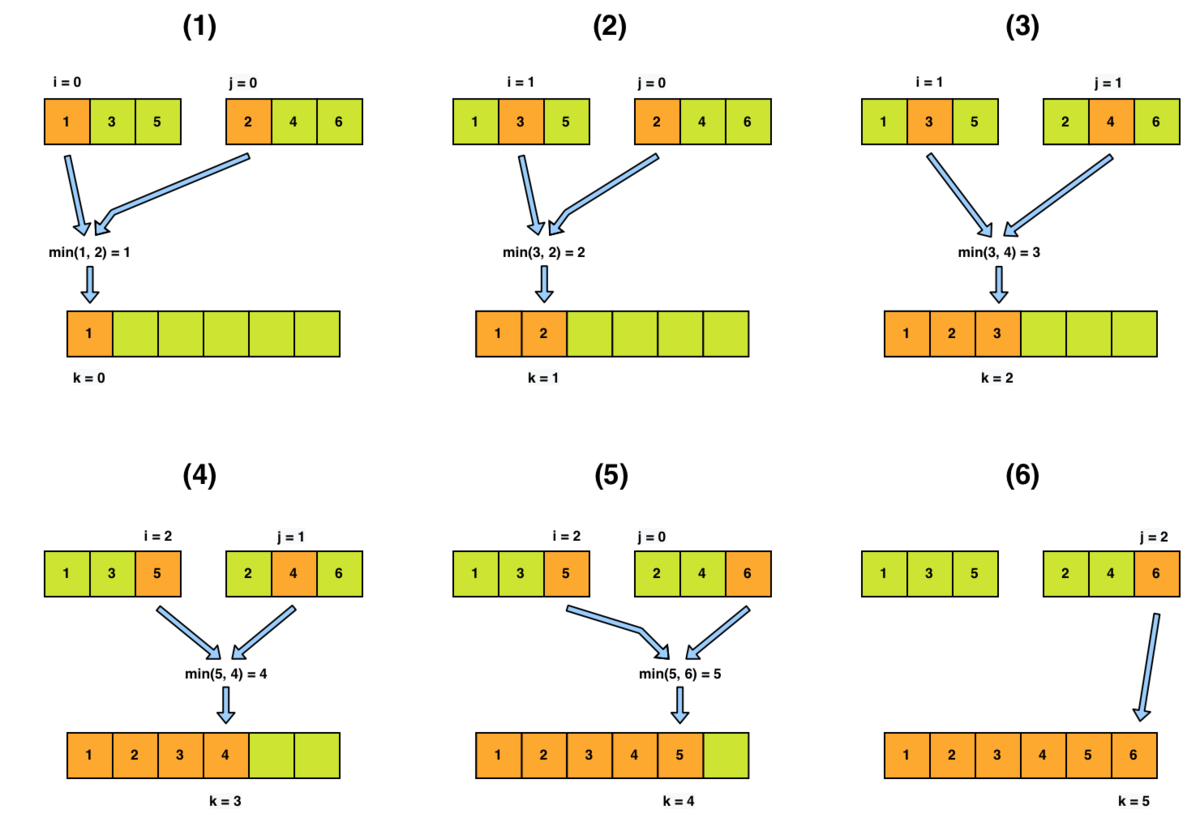
Vzorový príklad

Máme pole prvkov p = [1, 3, 5, 2, 4, 6], ktoré je už čiastočne utriedené. Použijeme algoritmus Merge, ktorý si vyptvorí pomocné polia p1 = [1, 3, 5] a p2 = [2, 4, 6]. Všetky polia indexujeme od 0, pričom pre pole p používame index k, pre p1 index i a p2 index j.

Vizualizácia funkcie Merge