Java - trieda Complex: Rozdiel medzi revíziami
| Riadok 1: | Riadok 1: | ||
{{Navigacne menu - java}} | {{Navigacne menu - java}} | ||
__TOC__ | __TOC__ | ||
| − | [[Súbor:komplexné číslo. | + | [[Súbor:komplexné číslo.png|left|thumb|Vizualizácia komplexného čísla]] |
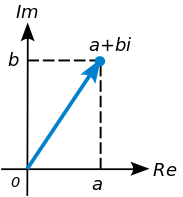
Komplexné čísla majú dôležitú úlohu technických disciplínach ako sú napríklad matematika, fyzika, elektrotechnika a iné. Zavedenie komplexných čísel nám dovoľuje riešiť úlohu, ktoré boli dovtedy neriešiteľné. Ako najjednoduchší prípad taktejto rovnice je <math>x^2+1=0</math>. Z tejto rovnice vychádza aj samotná definícia komplexného čísla. Komplexná jednotka i je definovaná ako: | Komplexné čísla majú dôležitú úlohu technických disciplínach ako sú napríklad matematika, fyzika, elektrotechnika a iné. Zavedenie komplexných čísel nám dovoľuje riešiť úlohu, ktoré boli dovtedy neriešiteľné. Ako najjednoduchší prípad taktejto rovnice je <math>x^2+1=0</math>. Z tejto rovnice vychádza aj samotná definícia komplexného čísla. Komplexná jednotka i je definovaná ako: | ||
| Riadok 100: | Riadok 100: | ||
Komplexné číslo môžeme vyjadriť súradnicami - reálna a imaginárna časť, ale aj vzdialenosťou od čísla 0 a uhlom, ktorý zviera s reálnou osou. | Komplexné číslo môžeme vyjadriť súradnicami - reálna a imaginárna časť, ale aj vzdialenosťou od čísla 0 a uhlom, ktorý zviera s reálnou osou. | ||
| − | [[Súbor:komplexné číslo 2. | + | [[Súbor:komplexné číslo 2.png|center|frame|Vyjadrenie komplexného čísla pomocou jeho veľkosti a uhla <math>\phi</math>]] |
Označmi si absolútnu hodnotu komplexného čísla 9X=a+bi) ako R. Pre výpočet R použijeme Pytagorovu vetu: | Označmi si absolútnu hodnotu komplexného čísla 9X=a+bi) ako R. Pre výpočet R použijeme Pytagorovu vetu: | ||
| Riadok 187: | Riadok 187: | ||
| − | [[Súbor:komplexne združené číslo. | + | [[Súbor:komplexne združené číslo.png|center|frame|Komplexne združené číslo]] |
Implementácia v Jave: | Implementácia v Jave: | ||
Aktuálna revízia z 11:54, 15. marec 2013
Základy informatiky - jazyk Java
Úvod do programovania v jazyku Java
Java - objektovo orientovaný prístup
Vzorové príklady:
Java - implementácia numerických algoritmov
Java - triedy geometrických tvarov
Pokročilé témy:
Obsah
Komplexné čísla majú dôležitú úlohu technických disciplínach ako sú napríklad matematika, fyzika, elektrotechnika a iné. Zavedenie komplexných čísel nám dovoľuje riešiť úlohu, ktoré boli dovtedy neriešiteľné. Ako najjednoduchší prípad taktejto rovnice je [math]x^2+1=0[/math]. Z tejto rovnice vychádza aj samotná definícia komplexného čísla. Komplexná jednotka i je definovaná ako:
[math]i=\sqrt{-1}[/math]
Komplexé číslo pozostáva z reálnej časti a imaginárnej časti: [math]A=a+bi[/math].
Trieda Complex
Pre prácu s komplexnými číslami v jazyku Java si vytvoríme novú triedu - Complex. Táto trieda bude reprezentovať jedno komplexné číslo. Trieda Complex bude obsahovať 2 vnútorné premenné reprezentujúce reálnu a imaginárnu časť komplexného čísla. Ďalej bude obsahovať metódy pre prácu s komplexnými číslami ako sú napríklad sčítavanie, násobenie, delenie komplexných čísel, ďalej metódy, ktoré zistia absolútnu hodnotu komplexného čísla alebo argument komplexného čísla.
Štruktúra celej triedy ja následovná:
public class Complex{
private double Re,Im;
// konstruktory
// pristupove metody
// ostatne metody
}
Konštruktory triedy Complex
Pre triedu Complex si vytvoríme si viacero konštruktorov. Ako prvý bude implicitný konštruktor bez parametrov. Tento konštruktor vytvorí nové komplexné číslo a do reálnej aj imaginárnej časti vloží hodnoty 0. Teda, nové komplexné číslo bude mať hodnotu 0+0i.
public Complex()
{
this.Re=0;
this.Im=0;
}
Ďalší konštruktor bude konverzný konštruktor s 2-mi parametrami. Podľa hodnoty parametrov bude mať hodnotu aj novo vytvárané komplexné číslo.
public Complex(double a, double b)
{
this.Re=a;
this.Im=b;
}
Tretí konštruktor bude konzerzný konštruktor, teda taký ktorý vytvorí nové komplexné číslo z už existujúceho komplexného čísla tak, že skopíruje jeho hodnoty reálnej a imaginárnej časti.
public Complex(Complex X)
{
this.Re=X.Re;
this.Im=X.Im;
}
Všimnime si, že vo všetkých konštruktoroch je rovnaký kód pre vytváranie komplexného čísla. Ponechajme si teda len jednu kompletnú definíciu a pri ostatných konštruktoroch sa odkazujme na túto definíciu. Najuviverzálnejší konštruktor je v našom prípade konverzný konštruktor, ktorý má dva paramtre. Pri ostatných konštruktoroch budeme teda volať na tento konštruktor pomocou kľúčového slova this. Samozrejme, musíme uviesť parametre v tomto konštruktore. Ešte raz uvedieme zoznam konštruktorov aj s elimináciou duplicitného kódu v konštruktoroch:
public Complex()
{
this(0,0);
}
public Complex(double a, double b)
{
this.Re=a;
this.Im=b;
}
public Complex(Complex X)
{
this(X.Re, X.Im);
}
settery
Pre triedu Complex definujme jednu metódu, ktorá nastaví nové hodnotu v reálnej aj imaginárnej čsti komplexného čísla:
public void setComplex(double a, double b){
this.Re=a;
this.Im=b;
}
gettery
Keďže vlastnosti (Re, Im) triedy Complex sú privátne, potrebujeme k nim prístupové metódy zvlášť k reálnej a zvlášť k imaginárnej časti komplexného čísla. Metódy sú veľmi jednoduché a nepotrebujú ani dodatočný výklad.
public double getRe(){
return this.Re;
}
public double getIm(){
return this.Im;
}
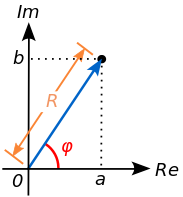
Komplexné číslo môžeme vyjadriť súradnicami - reálna a imaginárna časť, ale aj vzdialenosťou od čísla 0 a uhlom, ktorý zviera s reálnou osou.
Označmi si absolútnu hodnotu komplexného čísla 9X=a+bi) ako R. Pre výpočet R použijeme Pytagorovu vetu:
[math]R=\sqrt{a^2+b^2}[/math]
Uhol [math]\phi[/math] vypočítame pomocou goniometrických funkcií ako:
[math]\phi = arctan{\frac{b}{a}}[/math]
V našej triede Complex je riešenie jednoduché, stačí si uvedomiť, že a je reálna časť a b je imaginárna časť komplexného čísla.
public double getR(){
return Math.sqrt( Math.pow(this.Re, 2)+Math.pow(this.Im, 2));
}
public double getFi(){
return Math.atan(this.Im/this.Re);
}
Druhá odmocnina je v Jave statická metóda sqrt triedy Math. Výraz Math.pow(x,y) je výpočet mocniny [math]x^y[/math]. Funckia arctan(x) (arcus tangens) je definovaná ako Math.atan(x).
Aritmetika komplexných čísel
Sčítanie (odčítanie) komplexných čísel Komplexné čísla sčítavame/odčítavame tak, že sčítame/odčítame zvlášť ich reálne a zvlášť ich imaginárne časti. Majme komplexné čísla X a Y a vypočítajme Z=X+Y:
X=a+ib
Y=c+id
Z= X+Y = (a+c) + i(b+d)
Implemetácia v Jave:
public Complex add(Complex Y){
Complex Z=new Complex();
Z.Re=this.Re+Y.Re;
Z.Im=this.Im+Y.Im;
return Z;
}
public Complex add(double y){
Complex Z=new Complex();
Z.Re=this.Re+y;
Z.Im=this.Im;
return Z;
}
V druhom prípade uvažujeme o súčte komplexného čísla a reálneho čísla.
Násobenie komplexný čísel
Pri násobení komplexných čísel násobíme tak, ako keby boli komplexné čísla polynómy. Teda každú časť prvého komplexného čísal s každou časťou druhého komplexného čísla. Opäť si ukážeme príklad, ale teraz budeme požítať Z=X*Y:
X=a+ib
Y=c+id
Z= X*Y = (a+ib) + (c+id)
= a*c +i*a*d + i*b*c + i*i*d*b
= (a*c-d*b) + i(a*d + b*c)
Poznámka: vieme, že komplexná jednotka je definované ako [math]i=\sqrt{-1}[/math], preto [math]i^2=-1[/math]
Implemetácia v Jave:
public Complex mult(Complex Y){
Complex Z=new Complex();
Z.Re=(this.Re*Y.Re - this.Im*Y.Im);
Z.Im=(this.Im*Y.Re + this.Re*Y.Im);
return Z;
}
public Complex mult(double y){
Complex Z=new Complex();
Z.Re=this.Re * y;
Z.Im=this.Im * y
return Z;
}
V druhom prípade uvažujeme o súčine komplexného čísla a reálneho čísla.
Podiel komplexných čísel
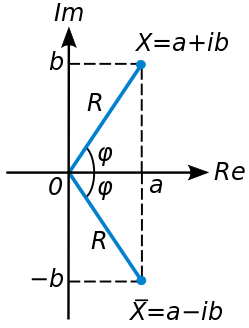
Komplexné čísla sa nedajú deliť, avšak vieme si ich upraviť tak, aby v delenec nebol komplexné číslo, ale len reálne číslo. Pred tým si ale definujme metódu, ktorá vypočíta komplexne združené (konjungované) číslo ku komplexnému číslu X. Nasledujúci obrázok ilustruje komplexné číslo X a komplexne združené číslo ku číslu X. Len poznamenáme, že jedinou zmenou je zman znamienka v imaginárnej časti komplexného čísla.
Implementácia v Jave:
public void conj(){
this.Im*=-1;
}
Podiel dvoch komplexných čísel X a Y môžeme vyjadriť nasledovne:
[math]X=a+bi\,[/math]
[math]Y=c+di\,[/math]
[math]Z=\frac{X}{Y}=\frac{X}{Y}*\frac{\bar{Y}}{\bar{Y}}=\frac{X*\bar{Y}}{Y*\bar{Y}}=\frac{X*\bar{Y}}{c^2+d^2}[/math]
Implementácia v Jave:
public Complex div(Complex Y) {
Complex Z = new Complex();
double menovatel = Y.Re * Y.Re + Y.Im * Y.Im;
Y.conj();
Z = this.mult(Y);
Z.mult(1 / menovatel);
return Z;
}
Umocňovanie komplexných čísel
Komplexné číslo sa dá vyjariť pomocou reálnej a imaginárnej časti
[math]X= a + bi\,[/math],
ale aj s pomocou absolútnej hodnoty a uhla [math]\phi[/math].
[math]X=R*(\cos{\phi}+i\sin{\phi}) \,[/math]
Z tohto zápisu je zrejmé, že
[math]a=R*\cos{\phi}\,[/math]
[math]b=R*\sin{\phi}\,[/math]
V tomto zápise je veľmi jednoduché vypočítať ľubovoľnú mocninu čísla X. Umocňovanie je totižto definované ako:
[math]X^n=R^n*(\cos{n\phi}+i\sin{n\phi}) \,[/math]
Implementácia v Jave:
public Complex pow(double n) {
double r, fi;
r = Math.pow(this.getR(), n);
fi = this.getFi() * n;
Complex Z = new Complex();
Z.setComplex(r * Math.cos(fi), r * Math.sin(fi));
return Z;
}
Pre úplnosť uveďme ešte preťaženú metódu toString
public String toString(){
String x=String.valueOf(this.Re);
if(this.Im<0)
x+=" -i"+this.Im*-1;
else
x+=" +i"+this.Im;
return x;
}
Použitie triedy Complex
Triedu Complex môžeme použiť v ľubovoľnej ďalšej aplikácii. Tu si ukážeme spôsob, použitia v najjednoduchšom prípade - konzolovej aplikácie. Komentár k použitiu bude uvedený priamo v zdrojovom kóde.
public static void main(String[] args){
// zavola sa implicitny konstruktor
Complex X=new Complex();
// zavola sa konverzny konstruktor
Complex Y=new Complex(2,-3);
// zavola sa kopirovaci konstruktor
Complex Z=new Complex(X);
//pouzitie metody pre nastavenie novej hodnoty
// komplexneho cisla
X.setComplex(-4,5);
// scitanie: Z=X+Y
Z=X.add(Y);
System.out.println(Z);
// nasobenie: Z=X*Y
Z=X.mult(Y);
System.out.println(Z);
// delenie: Z=X/Y
Z=X.div(Y);
System.out.println(Z);
// umocnenie: Z=X^3
Z=X.pow(3);
System.out.println(Z);
}
Výpis programu:
-2.0 +i2.0 7.0 +i22.0 -1.769 -i0.1538 236.00 +i114.99