Java applety - fraktály: Rozdiel medzi revíziami

Z Kiwiki
Skočit na navigaci Skočit na vyhledávání
(Vytvorená stránka „{{Navigacne menu - java}} V tejto časti budeme pracovať už s vytvorenou triedou Complex a využijeme ju pri zisťovaní vlastností komplexný…“)
 
 
Riadok 160: Riadok 160:
  
 
Pri posledných obrázkoch je vidieť formovanie určitého tvaru. Tento tvar má názov Júliuova množina<ref>http://en.wikipedia.org/wiki/Julia_set</ref>, čo je fraktál.
 
Pri posledných obrázkoch je vidieť formovanie určitého tvaru. Tento tvar má názov Júliuova množina<ref>http://en.wikipedia.org/wiki/Julia_set</ref>, čo je fraktál.
 +
==Fraktál 2 - Júliova množina==
 +
Od predchádzajúceho príkladu ku skutočnému fraktálu je len kúsok. Júliova množina je definovaná komplexnou funkciou
 +
 +
<math>f(z)=z^2+c\,</math>
 +
 +
kde ''c'' je komplexné číslo.
 +
 +
Urobne nasledujúce úpravy v definovaní farby pixelu: po skončení iterácie, kde počítame komplexnú funkciu (v našom prípade <math>f(z)=z^2-1</math>) určíme farbu nasledovne:
 +
*ak po n interáciách bude absulútna hodnota komplexného čísla z menšia ako 2, dané komplexné číslo patrí do Júliovej množiny a daný pixel ofarbíme čiernou farbou.
 +
*v opačnom prípade určíme farbu, ktorá bude úmerná počtu iterácií, kedy hodnota komplexnej funkcie nadobudla hodnotu väčšiu ako 2.
 +
 +
<source lang="java">
 +
public class Fraktal extends Applet {
 +
    private Complex z;
 +
    private double a;
 +
 +
    public void init() {
 +
        this.setSize(400, 400);
 +
        this.a = 2;
 +
        z = new Complex();
 +
    }
 +
 +
    public void paint(Graphics g) {
 +
        double krok = (2 * a) / this.getWidth();
 +
        int x, y; // pixely
 +
        double i, j; //realne hodnoty pre Complexne cisla
 +
        float h, s, v;
 +
        Color b;
 +
        Complex c = new Complex(-0.8,0.156);
 +
        int k, limit = 80;
 +
        for (i = -a, x = 0; i < a; i += krok, x++) {
 +
            for (j = -a, y = 0; j < a; j += krok, y++) {
 +
                z.setComplex(i, j);
 +
 +
                for (k = 0; k < limit; k++) {
 +
                    z = z.pow(2);
 +
                    z = z.add(c);
 +
                    if (z.getR() > 2) {
 +
                        break;
 +
                    }
 +
                }
 +
                b = selectColor(k, limit);
 +
                g.setColor(b);
 +
                g.drawLine(x, y, x, y);
 +
            }
 +
        }
 +
    }
 +
 +
    protected Color selectColor(int num_iterations, int max_iterations) {
 +
 +
        if (num_iterations >= max_iterations) {
 +
            return Color.black;
 +
        } else {
 +
            float h = (float) ((Math.tanh(num_iterations / 60.0) + 1) / 2.0);
 +
            return new Color(Color.HSBtoRGB(h, 1, 1));
 +
        }
 +
    }
 +
}
 +
 +
</source>
 +
 +
Metóda ''selectColor'' určuje farbu vykresľovania konkrétneho pixela na základe počtu iterécií, kedy absolútna hodnota komplexnej funkcie f(z) presiahne hodnotu 2.
 +
 +
[[Súbor:fraktál Julia set 1.png|thumb|300px|center|Júliova množina, kde c=-0.8+i0.156]]
 +
 +
[[Súbor:fraktál Julia set 2.png|thumb|300px|center|Júliova množina, kde c=-0.70176-i0.3842]]
 +
 +
[[Súbor:fraktál Julia set 3.png|thumb|300px|center|Júliova množina, kde c=-0.4+0.6i]]
 +
 +
==Fraktál 2 - Mandelbrotova množina==
 +
Platí to isté ako pre Júliovu množinu, ale hodnota komplexnej funkcie sa počíta odlišne. Pre Mandelbrotovu množinu je definované komplexná funkcia
 +
 +
<math>f(z)=z^2+c\,</math>
 +
 +
kde ''c'' je komplexné číslo.
 +
 +
Spôsob výpočtu hodnoty funkcie f(z):
 +
*hodnota ''z'' je vždy 0+i0,
 +
*hodnota ''c'' je definovaná bodom komplexnej roviny pre ktorý počítame hodnotu komplexnej funkcie f(z),
 +
*spôsob určenia farby je rovnaký.
 +
 +
Uvádzame len výpis metódy ''paint()''
 +
 +
<source lang="java">
 +
    public void paint(Graphics g) {
 +
        double krok = (2 * a) / this.getWidth();
 +
        int x, y; // pixely
 +
        double i, j; //realne hodnoty pre Complexne cisla
 +
        float h, s, v;
 +
        Color b;
 +
        Complex c = new Complex();
 +
        int k, limit = 80;
 +
        for (i = -a, x = 0; i < a; i += krok, x++) {
 +
            for (j = -a, y = 0; j < a; j += krok, y++) {
 +
                z.setComplex(0,0);
 +
                c.setComplex(i, j);
 +
                for (k = 0; k < limit; k++) {
 +
                    z = z.pow(2);
 +
                    z = z.add(c);
 +
                    if (z.getR() > 2) {
 +
                        break;
 +
                    }
 +
                }
 +
                b = selectColor(k, limit);
 +
                g.setColor(b);
 +
                g.drawLine(x, y, x, y);
 +
            }
 +
        }
 +
    }
 +
</source>
 +
 +
[[Súbor:fraktál Mandelbrot set 1.png|thumb|300px|center|Mandelbrotova množina]]
 +
 +
[[Súbor:fraktál Mandelbrot set 2.png|thumb|300px|center|Mandelbrotova množina, a=0.7]]
 
==Zdroje a odkazy==
 
==Zdroje a odkazy==
 
<references/>
 
<references/>

Aktuálna revízia z 23:12, 18. február 2011

Základy informatiky - jazyk Java

Platforma Java - prehľad

Úvod do programovania v jazyku Java

Java - objektovo orientovaný prístup

Vzorové príklady:

Prvé programy v Jave

Vzorové triedy v Jave

Java applety

>Java applety - základná práca
>Java applety - interakcia s používateľom
>Java applety - fraktály
>Java applety - animácia
>Java applety - animácie bez blikania

Java - desktopové aplikácie

Java - implementácia numerických algoritmov

Java - triedy geometrických tvarov

Pokročilé témy:

Základy práce s NetBeans IDE a vývoj modulov

V tejto časti budeme pracovať už s vytvorenou triedou Complex a využijeme ju pri zisťovaní vlastností komplexných čísel. V nasledujúcom texte bude ukázaný spôsob tvorvy fraktálov. V tomto prípade sa bude jednať o vyšetrovanie vlastností komplexných čísel na určitej oblasti v komplexnej rovine. Fraktál v našom podaní bude bitová mapa, ktorej pixely budú ofarbené podľa hdonoty komplxného čísla, ktoré pripadá na tento fraktál. Hlavou úlohou v celom procese vykresľovania je vhodne určiť farbu vykresľovania.

Aplikáciu budeme vytvárať ako applet (trieda java.applet.Applet).

Fraktál 1 - pokus o fraktál

Celý proces vytvárania si rozdeľme do jednoduchých krokov:

Vytvorenie appletu

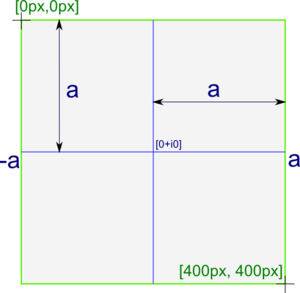
Vo vývojovom prostredí si vytvorme nový applet. Obrázok fraktálu budeme vykresľovať na celú jeho plochu. Predpokladom bude, že táto plocha bude vždy štvorcová, teda šírka plochy bude rovnaká ako jej výška. Jej veľkosť sa dá nastaviť v metóde init pomocou volania metódy setSize(). V našom prípade nastavíme rozmery na 400px × 400px.

Ďalšia vec ktorú potebujeme definovať je oblasť na komplexnej rovine, kde budeme skúmať vlstnosti komplexných čísel pri určitých operáciách. Táto oblasť bude taktiež vždy štvorcového tvaru so stranou 2*a (a=2). Budeme teda skúmať komplexné čísla na oblasti od (-2-i2) po (2+i2).

Veľkosť kresliacej plochy a oblasť na komplexnej rovine ilustreuje nasledujúci obrázok:

Zobrazenie rozmerov appletu a zobrazovanej oblasti komplexnej roviny

Keďže budeme pracovať s komplexnými číslami, v triede appletu Fraktal deklarujeme objekt z (typu Complex) a v metóde init ho inicializujeme.

V nasledujúcom zdrojovom kóde sú tieto poznaky zapísané: 

import java.applet.Applet;
import java.awt.Color;
import java.awt.Graphics;

public class Fraktal extends Applet {
    private Complex z;
    private double a;

    public void init() {
        this.setSize(400, 400);
        this.a = 2.0;
        z = new Complex();
    }

    public void paint(Graphics g) {
    }
}

Určenie farby pri vykresľovaní fraktálu

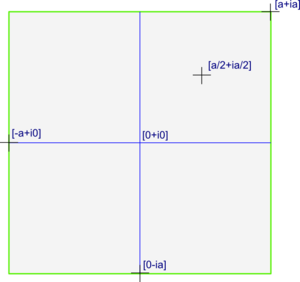
Každý pixel a applete predstavuje jedno komplexné číslo (ako je ukázané na nasledujúcom obrázku).

Zobrazenie komplexných čísel v komplexnej rovine

Farbu daného pixelu budú určovať vlastnosti komplexného čísla, ktoré je daným pixelom reprezentované. Pre určenie farby je vhodný farebný model HSV[1]. Na rozdiel od farebného modelu RGB, kde sa určuje podiel červenej, zelenej a modrej farby, v modeli HSB sa určuje odtieň (Hue), sýtosť (Saturation) a intezita (Value) farby.

Pre určenie farby môžeme postupovať rôznymi spôsobmi.

Farby fraktálu - model A

Skúsme nasledujúci spôsob ododenia farby pixelu (pixel reprezentuje komplexné číslo na danej pozícii)

  • odtieň (H) bude úmerný uhlu [math]\phi[/math] komplexného čísla,
  • sýtosť (S) bude úmerná veľkosti komplexného čísla,
  • intenzita (V) bude vždy 1

Všetky 3 hodnoty musia byť v intervale <0,1>. Uhol [math]\phi[/math] je v rozmedzí [math](-\frac{\pi}{2},\frac{\pi}{2})[/math], veľkosť komplexného čísla je úmerná hodnote a a je v intervale [math](0,\sqrt{2}a)[/math]

Táto transformácia hodnôt je jednoduchá. V prípade uhla [math]\phi[/math] stačí k hodnote [math]\phi[/math] pripočítať PI/2, čím dostaneme interval [math](0,2\pi)\,[/math] a túto hodnotu vydeliť hodnotu 2PI, čím dostaneme hodnoty z intervalu (0,1).

Pritransormácii veľkosti komplexného čísla na hodnotu z intervalu (0,1) môžeme použiť funckiu hyberbolický tangens[2], ktorá má definičný obor množinu reálnych čísel a obor hodnôt interval (-1,1). Potom stači pripočítať hodnotu 1 a celé vydeliť hodnotou 2, čím oäť získame hodnotu z intervalu (0,1).

Farby fraktálu - model B

Určenie farby je niekedy umenie. Treba skúšať a hľadať tie správne vzťahy. Skúsme nasledujúce závislosti

  • odtieň (H) bude úmerný uhlu [math]\phi[/math] komplexného čísla,
  • sýtosť (S) bude úmerná sínusu uhla [math]\phi[/math]
  • intenzita (V) bude úmerná kosínusu uhla [math]\phi[/math]

Opäť je potrebné tieto hodnoty transformovať tak, aby sme dostali hdonoty na intervale (0,1). V prípade sínusu a kosínusu je úloha jednoduchá. Keďže obor hodnôt týchto funkcií je (-1,1) stačí k danej hodnote pripočítať hodnotu 1 a celé to vydeliť hodnotou 2.

Vykreslenie fraktálu

V metóde paint() si vytvoríme cyklus, pomocou ktorého prejdeme všetky pixely na applete. Pre každý pixel nastavíme adekvátnu hodnotu komplexného čísla. Podľa uhla [math]\phi[/math] veľkosti komplexného čísla určíme farbu vykresľovania daného pixelu.

Vysvetlenie k nasledujúcemu zdrojovému kódu:

  • a - interval na ktorom kreslíme fraktál
  • krok - premenná, ktorá reprezentuje číselnú hodnotu jedného pixelu. Ak máme a=2 a šírku appletu 400px, potom krok=2a/sirka=0.001,
  • x,y - súradnice pri vykresľovaní v pixeloch
  • i,j - súradnice v komplexnej rovine. Ich hodnoty sa pohybyjú v intervale (-a,a)
  • h,s,v - farebné zložky
  • b - farba, ktorú určíme jednou z predchádzajúcich metód výpočtu farby
    public void paint(Graphics g) {
        double krok = (2 * a) / this.getWidth();
        int x, y; 
        double i, j; 
        float h, s, v;
        Color b;

        for (i = -a, x = 0; i < a; i += krok, x++) {
            for (j = -a, y = 0; j < a; j += krok, y++) {
                z.setComplex(i, j);
                //Metoda A
                h = (float) ((z.getFi() + Math.PI) / (Math.PI * 2));
                s = (float) ((Math.tanh(z.getR()) + 1) / 2);
                v=1;
                   
                //Metoda B
                //h = (float) ((z.getFi() + Math.PI) / (Math.PI * 2));
                //s=(float) ((Math.cos(z.getFi()) + 1) / 2);
                //v=(float) ((Math.sin(z.getFi()) + 1) / 2);

                b = new Color(Color.HSBtoRGB(h, s, v));
                g.setColor(b);
                g.drawLine(x, y, x, y);
            }
        }
    }

V tomto prípade je farba pixelu odvodená od komplexnej funkcie f(z)=z.

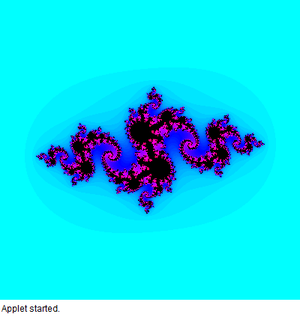
Výsledok

Farebný model A
Farebný model B

Blížšie k fraktálu

Namiesto komplexnej funkcie f(z)=z si zoberme funkcie [math]f(z)=z^2-1[/math]. V zdrojovom kóde sa za výraz z.setComplex(i, j), ktorý reprezentuje samotnú funkciu f(z)=z pridajú nasledujúce riadky: 

      z.setComplex(i, j); // tento riadok bol povodny
      z = z.pow(2);
      z = z.add(-1);

Výsledok

Farebný model A (z^2-1)
Farebný model B (z^2-1)


V ďalšej iterácii vylepšovania skúsme predchádzajúci kód niekoľkokrát zopakovať. V nasledujúcom zdrojovom kóde je počet iterácií výpočtu komplexnej funkcie 5. 

        for (i = -a, x = 0; i < a; i += krok, x++) {
            for (j = -a, y = 0; j < a; j += krok, y++) {
                z.setComplex(i, j);
  
                for (int k = 0; k < 5; k++) {
                    z = z.pow(2);
                    z = z.add(-1);
                }
  
                h = (float) ((z.getFi() + Math.PI) / (Math.PI * 2));
                s = (float) ((Math.tanh(z.getR()) + 1) / 2);
                v=1;

                b = new Color(Color.HSBtoRGB(h, s, v));
                g.setColor(b);
                g.drawLine(x, y, x, y);
            }
        }
Farebný model A (z^2-1), 5 iterácií
Farebný model B (z^2-1), 5 iterácií
Farebný model A (z^2-1), 15 iterácií
Farebný model B (z^2-1), 15 iterácií

Pri posledných obrázkoch je vidieť formovanie určitého tvaru. Tento tvar má názov Júliuova množina[3], čo je fraktál.

Fraktál 2 - Júliova množina

Od predchádzajúceho príkladu ku skutočnému fraktálu je len kúsok. Júliova množina je definovaná komplexnou funkciou

[math]f(z)=z^2+c\,[/math]

kde c je komplexné číslo.

Urobne nasledujúce úpravy v definovaní farby pixelu: po skončení iterácie, kde počítame komplexnú funkciu (v našom prípade [math]f(z)=z^2-1[/math]) určíme farbu nasledovne:

  • ak po n interáciách bude absulútna hodnota komplexného čísla z menšia ako 2, dané komplexné číslo patrí do Júliovej množiny a daný pixel ofarbíme čiernou farbou.
  • v opačnom prípade určíme farbu, ktorá bude úmerná počtu iterácií, kedy hodnota komplexnej funkcie nadobudla hodnotu väčšiu ako 2.
public class Fraktal extends Applet {
    private Complex z;
    private double a;

    public void init() {
        this.setSize(400, 400);
        this.a = 2;
        z = new Complex();
    }

    public void paint(Graphics g) {
        double krok = (2 * a) / this.getWidth();
        int x, y; // pixely
        double i, j; //realne hodnoty pre Complexne cisla
        float h, s, v;
        Color b;
        Complex c = new Complex(-0.8,0.156);
        int k, limit = 80;
        for (i = -a, x = 0; i < a; i += krok, x++) {
            for (j = -a, y = 0; j < a; j += krok, y++) {
                z.setComplex(i, j);

                for (k = 0; k < limit; k++) {
                    z = z.pow(2);
                    z = z.add(c);
                    if (z.getR() > 2) {
                        break;
                    }
                }
                b = selectColor(k, limit);
                g.setColor(b);
                g.drawLine(x, y, x, y);
            }
        }
    }

    protected Color selectColor(int num_iterations, int max_iterations) {

        if (num_iterations >= max_iterations) {
            return Color.black;
        } else {
            float h = (float) ((Math.tanh(num_iterations / 60.0) + 1) / 2.0);
            return new Color(Color.HSBtoRGB(h, 1, 1));
        }
    }
}

Metóda selectColor určuje farbu vykresľovania konkrétneho pixela na základe počtu iterécií, kedy absolútna hodnota komplexnej funkcie f(z) presiahne hodnotu 2.

Júliova množina, kde c=-0.8+i0.156
Júliova množina, kde c=-0.70176-i0.3842
Júliova množina, kde c=-0.4+0.6i

Fraktál 2 - Mandelbrotova množina

Platí to isté ako pre Júliovu množinu, ale hodnota komplexnej funkcie sa počíta odlišne. Pre Mandelbrotovu množinu je definované komplexná funkcia

[math]f(z)=z^2+c\,[/math]

kde c je komplexné číslo.

Spôsob výpočtu hodnoty funkcie f(z):

  • hodnota z je vždy 0+i0,
  • hodnota c je definovaná bodom komplexnej roviny pre ktorý počítame hodnotu komplexnej funkcie f(z),
  • spôsob určenia farby je rovnaký.

Uvádzame len výpis metódy paint() 

    public void paint(Graphics g) {
        double krok = (2 * a) / this.getWidth();
        int x, y; // pixely
        double i, j; //realne hodnoty pre Complexne cisla
        float h, s, v;
        Color b;
        Complex c = new Complex();
        int k, limit = 80;
        for (i = -a, x = 0; i < a; i += krok, x++) {
            for (j = -a, y = 0; j < a; j += krok, y++) {
                z.setComplex(0,0);
                c.setComplex(i, j);
                for (k = 0; k < limit; k++) {
                    z = z.pow(2);
                    z = z.add(c);
                    if (z.getR() > 2) {
                        break;
                    }
                }
                b = selectColor(k, limit);
                g.setColor(b);
                g.drawLine(x, y, x, y);
            }
        }
    }
Mandelbrotova množina
Mandelbrotova množina, a=0.7

Zdroje a odkazy

  1. ↑ http://en.wikipedia.org/wiki/HSL_and_HSV
  2. ↑ http://www.dplot.com/fct_tanh.htm
  3. ↑ http://en.wikipedia.org/wiki/Julia_set
Zdroj: „http://www.kiwiki.info/index.php?title=Java_applety_-_fraktály&oldid=9046“