Jazyk C (príklady) - Algoritmy: Rozdiel medzi revíziami
| Riadok 17: | Riadok 17: | ||
*orientované spojnice blokov | *orientované spojnice blokov | ||
[http://www.kiwiki.info/index.php/Algoritmus[Vývojové stavebné bloky]] | [http://www.kiwiki.info/index.php/Algoritmus[Vývojové stavebné bloky]] | ||
| + | |||
| + | |||
| + | ==Príklady== | ||
| + | |||
| + | ===Absolútna hodnota=== | ||
| + | Zadanie: Vieme, že absolútna hodnota je definovaná ako vzdialenosť čísla od začiatku súradnicového systému (resp. od nuly). Nakreslite vývojový diagram, ktorý by znázorňoval výpočet absolútnej hodnoty. | ||
| + | |||
| + | Analýza problému: Pre absolútnu hodnotu reálnych čísel platí: | ||
| + | |||
| + | abs(x) = x | ||
| + | abs(-x) = x | ||
| + | |||
| + | Inak povedané, pre x>=0, je absolútna hodnota x rovná práve x, pre x<0 je absolútna hodnota x rovná -1*x. | ||
| + | |||
| + | Teda, stačí nám zistiť, či je x menšie ako nula. | ||
| + | |||
| + | [[Súbor:78 2 alg1.png|240px|none]] | ||
Verzia zo dňa a času 12:41, 1. máj 2020
Riešené príklady
zdroj: Juraj Ďuďák, Zbierka úloh z algoritmizácie pre predmet Základy informatiky
ISBN: 978-80-8075-199-9
Obsah
V tejto kapitole budú ukázaná tvorba jednoduchých vývojových diagramov. Budú ukázané základné prvky algoritmizácie úloh, použitie rozhodovania, opakovania istého počtu operácií. K zvládnutiu tejto kapitoly sa predpokladá znalosť grafických značiek použitých pri tvorbe vývojových diagramov.
Grafické značky vývojových diagramov
Medzi základné stavebné bloky vývojových diagramov (VD) patria bloky, ktoré reprezentujú
- začiatok / koniec VD
- vykonávací blok
- rozhodovací blok
- spojka
- vstup / výstup dát
- orientované spojnice blokov
Príklady
Absolútna hodnota
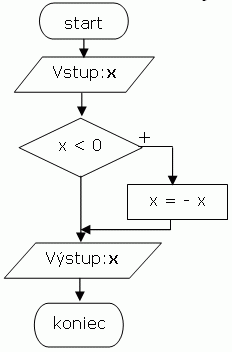
Zadanie: Vieme, že absolútna hodnota je definovaná ako vzdialenosť čísla od začiatku súradnicového systému (resp. od nuly). Nakreslite vývojový diagram, ktorý by znázorňoval výpočet absolútnej hodnoty.
Analýza problému: Pre absolútnu hodnotu reálnych čísel platí:
abs(x) = x abs(-x) = x
Inak povedané, pre x>=0, je absolútna hodnota x rovná práve x, pre x<0 je absolútna hodnota x rovná -1*x.
Teda, stačí nám zistiť, či je x menšie ako nula.