Popisná štatistika, bodové a intervalové odhady parametrov základného súboru, grafická prezentácia prvotných údajov: Rozdiel medzi revíziami
(Vytvorená stránka „=Popisná štatistika, bodové a intervalové odhady parametrov základného súboru, grafická prezentácia prvotných údajov= '''Štatistika''' Vyjadruje súhrn dát o…“) |
|||
| (Jedna medziľahlá úprava od jedného ďalšieho používateľa nie je zobrazená) | |||
| Riadok 1: | Riadok 1: | ||
| − | + | {{Kolokviálna skúška (hlavička)}} | |
'''Štatistika''' | '''Štatistika''' | ||
| Riadok 52: | Riadok 52: | ||
2. každej variante prisúdime početnosť | 2. každej variante prisúdime početnosť | ||
| + | [[Image:n.jpg|n.jpg]] | ||
Pre nespojitý znak veľkého počtu prípadne spojitý znak sa využívajú intervaly. Prvotná postupnosť –ako boli namerané tak sú postupne zapísané. | Pre nespojitý znak veľkého počtu prípadne spojitý znak sa využívajú intervaly. Prvotná postupnosť –ako boli namerané tak sú postupne zapísané. | ||
| Riadok 61: | Riadok 62: | ||
'''Absolútna početnosť''' – počet štatistických jednotiek pôvodného variačného rádu s rovnakou hodnotou | '''Absolútna početnosť''' – počet štatistických jednotiek pôvodného variačného rádu s rovnakou hodnotou | ||
| + | Pri spracovaní individuálnych údajov využívame zhusťovanie. | ||
| + | Pri zhusťovaní informácii zaznamenávame: | ||
| + | 1. Pri súbore malého rozsahu alebo prípadoch ak chceme aby individuálna hodnota mala svoje presné zastúpenie, číselnú charakteristiku z individuálnych hodnôt | ||
| + | 1,2,3,8,5,2...k | ||
| + | 520 :100= 5,2 aritmetický priemer | ||
| + | 2. Pri súbore väčšieho rozsahu viac ako 50 informácie zhusťujeme usporiadaním do skupín tzv. tried. Pri zhusťovaní dodržujeme pravidlá. | ||
| + | * prvok súboru zahrnieme do niektorej z tried, prvok musí byť zaradený len v jednej triede. | ||
| + | <1,3) | ||
| + | <3,5) | ||
| + | <5,7) | ||
| + | Variačné triedenie - je to usporiadanie štatistického súboru do tried podľa hodnôt daného kvantitatívneho znaku | ||
| + | *celkový počet štatistických jednotiek v štatistickom súbore sa rozdelí do k tried | ||
| + | 1. výpočet variačného rozpätia R = Xmax- Xmin | ||
| + | 2. Odhad vhodných počtov intervalov k | ||
| + | 3. Vypočítanie šírky intevalu n= R/k | ||
| + | 4. Vypočet hraníc intervalov | ||
| + | 5. Určíme triedne znaky/strednú hodnotu intervalu/ charakter. rovnosť/ | ||
| + | 6. Roztriedime jednotlivé hodnoty do príslušného invervalu | ||
| + | 7. Určíme absolútnu početnosť, relatívnu početnosť | ||
| + | '''Polygón''' závislosť relatívnej početnosti od príslušnej hodnoty štatistického znaku | ||
| + | |||
| + | [[Image:polygon.jpg|polygon.jpg]] | ||
| + | |||
| + | '''Histogram''' stĺpcový graf zobrazuje intervalové rozdelenie, zobrazí početnosť výskytu sledovaného znaku v určitom intervale prezentuje ho šírka stĺpca a početnosť náhodnej premennej v intervale x znázorňuje šírku stĺpika | ||
| + | |||
| + | [[Image:histogram.jpg|histogram.jpg]] Gaussova krivka- prezentuje ideal | ||
=Analýza požiadaviek zákazníka= | =Analýza požiadaviek zákazníka= | ||
Aktuálna revízia z 22:38, 17. marec 2011
Tento článok patrí do časti Kolokviálna skúška. Materiály tu uvedené sú prípravou na záverečnú štátnu (kolokviálnu) skúšku v študijnom zameraní Manažérstvo kvality produkcie na Fakulte mechatroniky TnUAD.
Štatistika Vyjadruje súhrn dát o hromadných javoch Činnosť smerujúca k získavaniu štatistických dát k ich usporiadaniu, spracovaniu a následné využívanie. Je to metodologická veda, ktorej cieľom je skúmanie zákonitosti hromadných javov, ktoré tvorí metodológia zisťovania, spracovania a analyzovania dát.
Hromadný jav – sa neustále opakuje (koľko krát sa opakuje vyjadruje kazovosť výrobku) Štatistické vyjadrenie skúmané poznatky hromadnými javmi. Štatistický súbor – je zložený zo štatistických jednotiek Štatistická jednotka – sú to jednotlivé objekty/prvky tohto súboru.
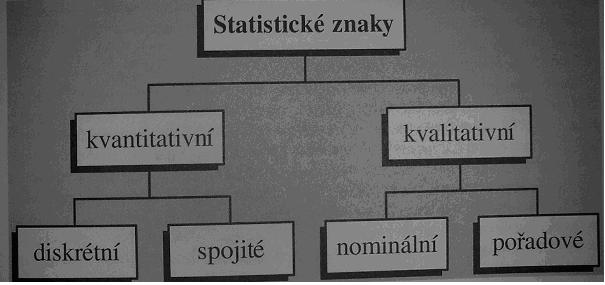
Skúmanie hromadných javov predpokladá definovanie z hľadiska účelu skúmania vymedzenie množiny prvkov skúmania. Rozsah súboru : je vlastne počet jednotiek súboru ( koľko budem skúmať) Základný súbor : sú súbory, ktoré sú predmetom skúmania Výberový súbor : skupinka, vzorka štatistických jednotiek Štatistický znak : vyjadruje merateľné vlastnosti štatistických jednotiek má dve roviny
- slovné (kvalitatívne)
- číselné (kvantitatívne) –(dĺžka, hmotnosť, šírka, hĺbka..)
Jednorozmerný súbor : práca v štatistickom súbore s jedným znakom
Viacrozmerný súbor : skúmania viacerých znakov
Štatistické skúmanie: 1etapa : štatistické zisťovanie – získavanie neznámych štatistických dát, ktorý charakterizujú daný súbor
- priestorové zisťovanie
- vecné zisťovanie
- časové zisťovanie
Ak dochádza k spracovaniu dát, dáta sa pre analýzu usporiadajú a zotriedia (triedenie-je rozdelenie jednotiek súboru do skupín, pričom musia vyniknúť charakteristickým vlastnostiam skúmaných javov) 1. Triedenie podľa obsahu skúmania *typologické *prehĺbené *analytické 2. Triedenie podľa počtu triediacich znakov *jednostupňové *viacstupňové 3. Triedenie podľa druhu triediacich znakov *časové hľadisko *miestne hľadisko 4. Triedenie podľa kvalitatívneho znaku *alternatívne *množné 5. Triedenie podľa kvantitatívneho znaku/variačné triedenie
Triediaci znak kvalitatívny s malým počtom obmien potom vhodným štatistickým usporiadaním sa nazýva frekvenčná tabuľka. 1. usporiadanie podľa veľkosti 2. každej variante prisúdime početnosť
Pre nespojitý znak veľkého počtu prípadne spojitý znak sa využívajú intervaly. Prvotná postupnosť –ako boli namerané tak sú postupne zapísané. xj= (j= 1,2....n) j-význam poradia zaznamenania
Rozsah súboru- počet prvkov prvotnej tabulky Variačný rád –štatistický súbor, ktorého hodnoty sú usporiadané podľa veľkosti Absolútna početnosť – počet štatistických jednotiek pôvodného variačného rádu s rovnakou hodnotou
Pri spracovaní individuálnych údajov využívame zhusťovanie. Pri zhusťovaní informácii zaznamenávame: 1. Pri súbore malého rozsahu alebo prípadoch ak chceme aby individuálna hodnota mala svoje presné zastúpenie, číselnú charakteristiku z individuálnych hodnôt 1,2,3,8,5,2...k 520 :100= 5,2 aritmetický priemer 2. Pri súbore väčšieho rozsahu viac ako 50 informácie zhusťujeme usporiadaním do skupín tzv. tried. Pri zhusťovaní dodržujeme pravidlá.
- prvok súboru zahrnieme do niektorej z tried, prvok musí byť zaradený len v jednej triede.
<1,3) <3,5) <5,7)
Variačné triedenie - je to usporiadanie štatistického súboru do tried podľa hodnôt daného kvantitatívneho znaku
- celkový počet štatistických jednotiek v štatistickom súbore sa rozdelí do k tried
1. výpočet variačného rozpätia R = Xmax- Xmin 2. Odhad vhodných počtov intervalov k 3. Vypočítanie šírky intevalu n= R/k 4. Vypočet hraníc intervalov 5. Určíme triedne znaky/strednú hodnotu intervalu/ charakter. rovnosť/ 6. Roztriedime jednotlivé hodnoty do príslušného invervalu 7. Určíme absolútnu početnosť, relatívnu početnosť
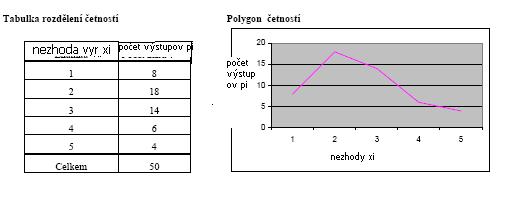
Polygón závislosť relatívnej početnosti od príslušnej hodnoty štatistického znaku
Histogram stĺpcový graf zobrazuje intervalové rozdelenie, zobrazí početnosť výskytu sledovaného znaku v určitom intervale prezentuje ho šírka stĺpca a početnosť náhodnej premennej v intervale x znázorňuje šírku stĺpika
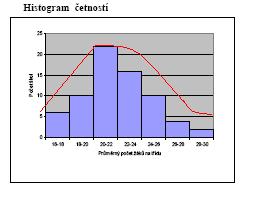 Gaussova krivka- prezentuje ideal
Gaussova krivka- prezentuje ideal