Amplitúdová a fázová charakteristika RC obvodu: Rozdiel medzi revíziami

Z Kiwiki
Skočit na navigaci Skočit na vyhledávání
(Vytvorená stránka „Aplitúdovú a fázovú charakteristiku jednoduchých obvodov môžeme získať tabeláciou komplexnej prenosovej funkcie obvodu. Skriptovací jazyk Python má priamu podp…“)
 
d
 
(9 medziľahlých úprav od jedného ďalšieho používateľa nie je zobrazených)
Riadok 1: Riadok 1:
 +
{{sablona_python_priklady|Elektronika}}
 +
__NOTOC__
 +
[[Category:Python]]
 
Aplitúdovú a fázovú charakteristiku jednoduchých obvodov môžeme získať
 
Aplitúdovú a fázovú charakteristiku jednoduchých obvodov môžeme získať
 
tabeláciou komplexnej prenosovej funkcie obvodu. Skriptovací jazyk Python  
 
tabeláciou komplexnej prenosovej funkcie obvodu. Skriptovací jazyk Python  
 
má priamu podporu pre prácu s komplexnými číslami a s pomocou  
 
má priamu podporu pre prácu s komplexnými číslami a s pomocou  
−
rozširujúcich balíkov ''scipy'' a ''pylab'' je možné výsledky analyzovať  
+
rozširujúceho balíka ''pylab''<ref>http://www.scipy.org/PyLab</ref>  (obsahuje podstatné časti balíkov ''scipy''<ref>http://www.scipy.org/</ref> a ''matplotlib''<ref>http://matplotlib.sourceforge.net/</ref>) je možné výsledky analyzovať  
 
a graficky zobraziť.
 
a graficky zobraziť.
  
−
'''Analýza obvodu'''
+
=== Analýza obvodu ===
  
−
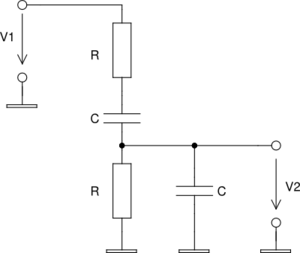
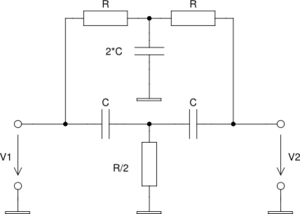
Pre analýzu obdu sme zvolili jednoduchý RC filter.
+
Pre všeobecnú analýzu obvodu sme zvolili jednoduchý pásmový RC filter. Tento obvod s konkrétnymi hodnotami komponentov je simulovaný pomocou simulátora ''gsim'' v článku [[RC_filtre]].
 +
 
 +
[[Súbor:py-rc-filter.png | thumb|center|300px | <div align="center"> Zapojenie RC obvodu </div>]]
  
−
[[Súbor:py-rc-filter.png]]
 
  
 
Pre nezaťažený výstup obvodu je možné odvodiť komplexnú prenosovú  
 
Pre nezaťažený výstup obvodu je možné odvodiť komplexnú prenosovú  
Riadok 27: Riadok 31:
 
         \hat{V_1}
 
         \hat{V_1}
 
</math>
 
</math>
 +
 +
Substitúciou pre bezrozmernú normovanú frekvenciu <math> \Omega = j \omega RC </math>  dostaneme
 +
 +
:<math>
 +
  \hat{A}(j \Omega) = \frac {\hat{V_2} }
 +
                            {\hat{V_1} }  =   
 +
        \frac{j \Omega} {(1+ 3j \Omega - \Omega^2)}
 +
</math>
 +
 +
Analyticky je možné vyjadriť amplitúdovú a fázovú charakteristiku v jednotkách normovanej frekvencie
 +
<math>\Omega</math> pomocou modulu a fázového posunu komplexnej prenosovej funkcie obvodu.
 +
 +
:<math>
 +
  \left| A  \right| =   
 +
        \frac{1} {\sqrt{ \left( \frac{1}{\Omega} - \Omega \right)^2  + 9}} 
 +
</math>
 +
 +
:<math>
 +
    \varphi =   
 +
        \arctan \frac {1-\Omega^2 }{3 \Omega} 
 +
</math>
 +
 +
=== Tabelácia prenosovej funkcie obvodu ===
 +
 +
V interaktívnom móde Pythonu (konzola, iPython<ref>http://ipython.github.com/ipython-doc/</ref>) importujeme balík ''pylab'' pre vedecké výpočty a vizualizáciu dát
 +
<source lang="python">
 +
>>> from pylab import *
 +
</source>
 +
 +
Pre tabeláciu funkcie vytvoríme pole s hodnotami normovanej frekvencie <math>\Omega</math> v logaritmickom rozsahu šiestich dekád príkazom
 +
<source lang="python">
 +
>>> omega=logspace(-3,3) 
 +
</source>
 +
 +
Z komplexnej prenosovej funkcie vypočítame amplitúdovú a fázovú charakteristiku
 +
pomocou funkcií '''abs''' a '''arctan'''. Všetky matematické operácie sa v Pythone pochopiteľne uskutočňujú nad poľami hodnôt.
 +
 +
<source lang="python">
 +
>>> A=1j*omega/(1+3j*omega-omega**2)
 +
>>> ampl=abs(A)
 +
>>> phase=arctan(A.imag/A.real)
 +
</source>
 +
 +
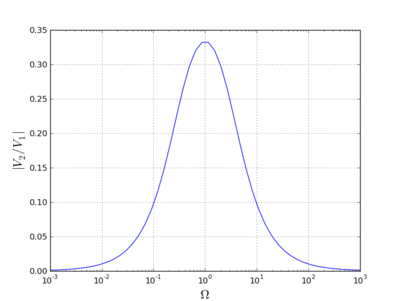
Aplitúdovú charakteristiku zobrazíme v semilogaritmickom grafe pomocou funkcie '''semilogx'''. Štandardná funkcia '''plot''' nie je na zobrazenie semilogaritmických dát bez ďaľších úprav vhodná. Podobne zobrazíme aj fázovú charakteristiku obvodu.
 +
 +
<source lang="python">
 +
>>> semilogx(omega,ampl)
 +
>>> grid()
 +
>>> show()
 +
</source>
 +
 +
Výsledok výpočtu sa zobrazí v interaktívnom prehliadači, graf môžete uložiť do súboru v rôznych formátoch.
 +
 +
[[Súbor:py-rc-ampl.png | thumb|center|400px | <div align="center"> Aplitúdová charakteristika </div>]]
 +
 +
 +
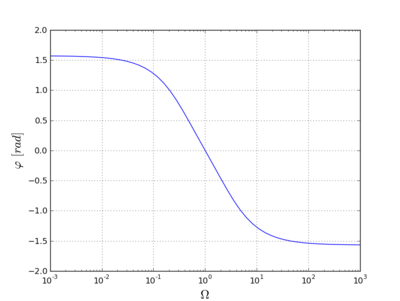
Podobným spôsobom môžete zobraziť aj fázovú charakteristiku obvodu. Pomocou funkcií z balíka ''matplotlib'' je možné grafy ďalej upravovať a popisovať.
 +
 +
[[Súbor:py-rc-phase.png | thumb|center|400px | <div align="center"> Fázová charakteristika </div>]]
 +
 +
=== Príklady a úlohy ===
 +
 +
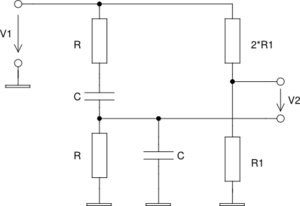
Na základe vyššie uvedeného postupu vypočítajte a zobrazte normované prenosové charakteristiky nasledujúcich obvodov.
 +
 +
[[Súbor:py-rc-ex1.png | thumb|center|300px | <div align="center"> Úloha 1. </div>]]
 +
 +
[[Súbor:py-rc-ex2.png | thumb|center|300px | <div align="center"> Úloha 2. </div>]]
 +
 +
=== Literatúra a odkazy ===
 +
<references/>

Aktuálna revízia z 10:37, 18. marec 2013

Tento príklad patrí pod predmet Základy informatiky - jazyk Python, časť Elektronika

Aplitúdovú a fázovú charakteristiku jednoduchých obvodov môžeme získať tabeláciou komplexnej prenosovej funkcie obvodu. Skriptovací jazyk Python má priamu podporu pre prácu s komplexnými číslami a s pomocou rozširujúceho balíka pylab[1] (obsahuje podstatné časti balíkov scipy[2] a matplotlib[3]) je možné výsledky analyzovať a graficky zobraziť.

Analýza obvodu

Pre všeobecnú analýzu obvodu sme zvolili jednoduchý pásmový RC filter. Tento obvod s konkrétnymi hodnotami komponentov je simulovaný pomocou simulátora gsim v článku RC_filtre.

Zapojenie RC obvodu


Pre nezaťažený výstup obvodu je možné odvodiť komplexnú prenosovú funkciu obvodu

[math] \hat{V_2}=\frac{ 1/[(1/R)+j \omega C] } {[1/(1/R) + j \omega C] + R + (1/ j \omega C) } \hat{V_1} [/math]

po úprave

[math] \hat{V_2}=\frac{ j \omega RC } {( j \omega RC + 1)^2 + j \omega R C } \hat{V_1} [/math]

Substitúciou pre bezrozmernú normovanú frekvenciu [math] \Omega = j \omega RC [/math] dostaneme

[math] \hat{A}(j \Omega) = \frac {\hat{V_2} } {\hat{V_1} } = \frac{j \Omega} {(1+ 3j \Omega - \Omega^2)} [/math]

Analyticky je možné vyjadriť amplitúdovú a fázovú charakteristiku v jednotkách normovanej frekvencie [math]\Omega[/math] pomocou modulu a fázového posunu komplexnej prenosovej funkcie obvodu.

[math] \left| A \right| = \frac{1} {\sqrt{ \left( \frac{1}{\Omega} - \Omega \right)^2 + 9}} [/math]
[math] \varphi = \arctan \frac {1-\Omega^2 }{3 \Omega} [/math]

Tabelácia prenosovej funkcie obvodu

V interaktívnom móde Pythonu (konzola, iPython[4]) importujeme balík pylab pre vedecké výpočty a vizualizáciu dát 

>>> from pylab import *

Pre tabeláciu funkcie vytvoríme pole s hodnotami normovanej frekvencie [math]\Omega[/math] v logaritmickom rozsahu šiestich dekád príkazom 

>>> omega=logspace(-3,3)

Z komplexnej prenosovej funkcie vypočítame amplitúdovú a fázovú charakteristiku pomocou funkcií abs a arctan. Všetky matematické operácie sa v Pythone pochopiteľne uskutočňujú nad poľami hodnôt. 

>>> A=1j*omega/(1+3j*omega-omega**2) 
>>> ampl=abs(A) 
>>> phase=arctan(A.imag/A.real)

Aplitúdovú charakteristiku zobrazíme v semilogaritmickom grafe pomocou funkcie semilogx. Štandardná funkcia plot nie je na zobrazenie semilogaritmických dát bez ďaľších úprav vhodná. Podobne zobrazíme aj fázovú charakteristiku obvodu. 

>>> semilogx(omega,ampl)
>>> grid() 
>>> show()

Výsledok výpočtu sa zobrazí v interaktívnom prehliadači, graf môžete uložiť do súboru v rôznych formátoch.

Aplitúdová charakteristika


Podobným spôsobom môžete zobraziť aj fázovú charakteristiku obvodu. Pomocou funkcií z balíka matplotlib je možné grafy ďalej upravovať a popisovať.

Fázová charakteristika

Príklady a úlohy

Na základe vyššie uvedeného postupu vypočítajte a zobrazte normované prenosové charakteristiky nasledujúcich obvodov.

Úloha 1.
Úloha 2.

Literatúra a odkazy

  1. ↑ http://www.scipy.org/PyLab
  2. ↑ http://www.scipy.org/
  3. ↑ http://matplotlib.sourceforge.net/
  4. ↑ http://ipython.github.com/ipython-doc/
Zdroj: „http://www.kiwiki.info/index.php?title=Amplitúdová_a_fázová_charakteristika_RC_obvodu&oldid=11388“