Algoritmy vyhľadávania: Rozdiel medzi revíziami

Z Kiwiki
Skočit na navigaci Skočit na vyhledávání
(Vytvorená stránka „Kategória:Študijné materiály Kategória:Programovanie Kategória:Informatika '''Vyhľadávanie''' Vyhľadávanie je základnou úlohou pri práci s väčš…“)
 
 
(18 medziľahlých úprav od 2 ďalších používateľov nie je zobrazených)
Riadok 1: Riadok 1:
−
[[Kategória:Študijné materiály]]
+
{{Draft}}
−
[[Kategória:Programovanie]]
+
{{Skripta programovanie}}
−
[[Kategória:Informatika]]
+
__TOC__
 +
{{Cvicenie|Vyhľadávanie (riešené príklady)}}
 
'''Vyhľadávanie'''
 
'''Vyhľadávanie'''
  
Riadok 8: Riadok 9:
 
#Vyhľadávanie v usporiadaných zoznamoch (resp. poliach)
 
#Vyhľadávanie v usporiadaných zoznamoch (resp. poliach)
 
#Vyhľadávanie v rekurzívnych štruktúrach
 
#Vyhľadávanie v rekurzívnych štruktúrach
 +
  
 
=Sekvenčné vyhľadávanie=
 
=Sekvenčné vyhľadávanie=
Riadok 87: Riadok 89:
  
 
=Vyhľadávanie v usporiadaných zoznamoch=
 
=Vyhľadávanie v usporiadaných zoznamoch=
 +
Zložitosť O(n) pre algorimy lineárneho, resp. sekvenčného vyhľadávania dokážeme znížiť, ak sú údaje v ktorých budeme vyhľadávať usporiadané. V tomto prípade nemusíme pole prvkov v ktorom hľadáme prechádzať celé (od indexu 0 až po n-1), ale stačí si skontrolovať položky len na určitých miestach.
 +
 
==Binárne vyhľadávanie==
 
==Binárne vyhľadávanie==
−
http://en.wikipedia.org/wiki/Binary_search
+
Predpoklad správneho vyhľadávania je, že prvku sú v poli usporiadané. Postup vyhľadávania:
 +
;Použité premenné:
 +
*''pole'' - jednorozmerné pole, v ktorom budeme vyhľadávať
 +
*''x'' - prvok, ktorý hľadáme
 +
*''n'' - veľkosť pola ''pole''.
 +
*''lavy'', ''pravy'' - rozsah poľa, (začiatok , koniec) kde budeme hľadať.
 +
 
 +
 
 +
#Rozdeľ pole na 2 polovice. Index stredného prvku vypočítaš ako:
 +
#* stred=(lavy+pravy)/2
 +
#Ak platí lavy>pravy, tak koniec, prvok sa nenašiel.
 +
#Zober prvok v strede poľa (na indexe stred) a porovnaj ho s hľadaným prvkom ''x''
 +
#Ak sa ''x'' zhoduje so stredným prvkom - koniec. Výsledok je index tohto prvku
 +
#V opačnom prípade
 +
#*Ak je ''x'' väčšie ako stredný prvok, tak hľadaj v pravej časti poľa
 +
#**lavy=stred+1, pravy zostava nezmenený (choď na krok 1)
 +
#*Ak je ''x'' menšie ako stredný prvok, tak hľadaj v ľavej časti poľa
 +
#**lavy=zostava nezmenený, pravy = stred-1 (choď na krok 1)
 +
 
 +
Ukážme si konkrétny príklad (šedé políčka predstavujú indexy poľa, biele sú prvky poľa):
 +
<source lang="c">
 +
x=18
 +
n=10
 +
</source>
 +
{| class="wikitable" border=1 cellpadding=5
 +
|+pole=
 +
|- style="color:green;background-color:#DADADA"
 +
|0 ||1 ||2 ||3 ||4 ||5 ||6 ||7 ||8 ||9 ||10
 +
|-
 +
|1 ||2 ||6 ||18 ||20 ||23 ||29 ||32 ||34 ||39 ||43
 +
|}
 +
Pre implementáciu algoritmu binárneho vyhľadávania si musíme vypočítať hodnoty ľavého a pravého indexu poľa, v ktorom hľadáme. Na začiatok je to jednoduché:
 +
<source lang="c">
 +
lavy=0
 +
pravy=n-1
 +
</source>
 +
*Porovnajme hľadaný prvok x=18 so stredným prvkom:
 +
<source lang="c">
 +
stred=(lavy+pravy)/2
 +
stred=5
 +
</source>
 +
{| class="wikitable" border=1 cellpadding=5
 +
|+pole=
 +
|- style="color:green;background-color:#DADADA"
 +
|0 ||1 ||2 ||3 ||4 ||5 ||6 ||7 ||8 ||9 ||10
 +
|-
 +
|style="background-color:yellow" |1
 +
|style="background-color:yellow" |2
 +
|style="background-color:yellow" |6
 +
|style="background-color:yellow" |18
 +
|style="background-color:yellow" |20
 +
|style="font-weight:800" | 23
 +
|style="background-color:gray" |29
 +
|style="background-color:gray"|32
 +
|style="background-color:gray"|34
 +
|style="background-color:gray"|39
 +
|style="background-color:gray"|43
 +
|}
 +
* pole[5] != x (23 != 18 )
 +
** platí že x<23 (resp. <nowiki>x<pole[stred])</nowiki>
 +
** budeme vyhľadávať vľavo (žltá časť)
 +
*** lavy zostane nezmeneny (0)
 +
*** pravy=stred - 1 <nowiki>(4)</nowiki>
 +
 
 +
*Porovnajme hľadaný prvok x=18 so stredným prvkom<nowiki>:</nowiki>
 +
 
 +
<source lang="c">
 +
stred=(lavy+pravy)/2 = (0+4)/2=2
 +
stred=2
 +
</source>
 +
 
 +
{| class="wikitable" style="border:1px solid black" cellpadding="5"
 +
|+pole=
 +
|- style="color:green;background-color:#DADADA"
 +
|0 ||1 ||2 ||3 ||4 ||5 ||6 ||7 ||8 ||9 ||10
 +
|-
 +
|style="background-color:gray" |1
 +
|style="background-color:gray" |2
 +
|style="font-weight:800" |6
 +
|style="background-color:yellow" |18
 +
|style="background-color:yellow" |20
 +
|style="background-color:gray" | 23
 +
|style="background-color:gray" |29
 +
|style="background-color:gray"|32
 +
|style="background-color:gray"|34
 +
|style="background-color:gray"|39
 +
|style="background-color:gray"|43
 +
|}
 +
 
 +
* pole[2] != x  (6 != 18 )
 +
** platí že x>6 (resp. x>pole[stred])
 +
** budeme vyhľadávať vpravo (žltá časť)
 +
*** lavy = stred + 1 (3)
 +
*** pravy zostane nezmeneny (4)
 +
 
 +
*Porovnajme hľadaný prvok x=18 so stredným prvkom:  
 +
<source lang="c">
 +
stred=(lavy+pravy)/2 = (3+4)/2=3
 +
stred=3
 +
</source>
 +
* pole[3] == x (18 = 18 )
 +
*Stredný prvok je zhodný s hľadaným
 +
*Algoritmus končí
 +
**Výsledok je index nájdeného prvku, teda ''stred''. V našom príklade je to 3.
 +
 
 +
===Binárne vyhľadávanie - zdrojový kód v jazyku C===
 +
<properties>
 +
Názov funkcie=hladajBinarne<br/>hladajBinarneR
 +
Návratová hodnota=index nájdeného prvku (-1 pri neúspechu)
 +
Parametre=pole prvkov - pole<br/>rozmer poľa - n<br/>hľadaný prvok - x
 +
Zložitosť algoritmu=O(Log(n))
 +
</properties>
 +
 
 +
Keďže samotné definícia binárneho vyhľadávania je rekurzívna, uvádzame aj rekurzívnu verziu funkcie.
 +
 
 +
 
 +
'''Iteračná verzia'''
 +
<source lang="c">
 +
int hladajBinarne(int *pole,int dlzka, int x)
 +
{ int najdene=0;
 +
int lavy = 0, pravy = dlzka - 1, stred;
 +
while ( (lavy <= pravy) && (najdene==0) )
 +
{
 +
  stred = (lavy + pravy) / 2;
 +
  if (pole[stred] == x)
 +
najdene=1;
 +
  else
 +
    if (pole[stred] < x)
 +
    lavy = stred + 1;
 +
  else
 +
    pravy=stred - 1;
 +
}
 +
if(najdene==1)
 +
return stred;
 +
else
 +
return -1;
 +
}
 +
 
 +
</source>
 +
'''Rekurzívna verzia'''
 +
<source lang="c">
 +
int hladajBinarneR(int *pole,int lavy, int pravy, int x)
 +
{  if(lavy>pravy)
 +
return -1;
 +
else
 +
{
 +
int stred=(lavy+pravy)/2;
 +
if(pole[stred]==x)
 +
  return stred;
 +
else
 +
{  if( x<pole[stred] )
 +
return hladajB(pole,lavy,stred-1,x);
 +
  else
 +
return hladajB(pole,stred+1,pravy,x);
 +
}
 +
}
 +
}
 +
 
 +
</source>
 +
 
 
==Ternárne vyhľadávanie==
 
==Ternárne vyhľadávanie==
−
http://en.wikipedia.org/wiki/Ternary_search
+
Predpoklad správneho vyhľadávania je, že prvku sú v poli usporiadané. Postup vyhľadávania je podobný ako pri binárnom vyhľadávaním abšak pole nerozdelíme na polovicu ale na tretiny.
−
==Interpolačné vyhľadávanie==
+
 
−
http://en.wikipedia.org/wiki/Interpolation_search
+
;Použité premenné:
 +
*''pole'' - jednorozmerné pole, v ktorom budeme vyhľadávať
 +
*''x'' - prvok, ktorý hľadáme
 +
*''n'' - veľkosť pola ''pole''.
 +
*''i'', ''j'' - rozsah poľa, (začiatok , koniec) kde budeme hľadať.
 +
*''m1'' - index prvku v prvej tretine
 +
*''m2'' - index prvku v druhej tretine
 +
 
 +
 
 +
#Rozdeľ pole na tretiny
 +
##m1=( i*2 + j ) / 3;
 +
##m2=( i + j*2 ) / 3;
 +
#Porovnaj, či sa hľadaný prvok zhoduje z prvkom na indexe m1, ak áno, tak koniec. Výsledok je index m1
 +
#Porovnaj, či sa hľadaný prvok zhoduje z prvkom na indexe m2, ak áno, tak koniec. Výsledok je index m2
 +
#Ak platí i>j, skonči, prvok x sa v poli nenachádza.
 +
#Ak je hľadaný prvok menší ako prvok pole[m1], tak hľadaj v prvej tretine poľa
 +
#* i zostáva nezmenené , j=m1-1. Choď na krok 1.
 +
#Ak je hľadaný prvok väčší ako prvok pole[m2], tak hľadaj v tretej tretine poľa
 +
#* i = m2+1 , j zostáva nezmenené. Choď na krok 1.
 +
#inak hľadaj v druhej tretine poľa
 +
#* i = m1+1 , j=m2-+. Choď na krok 1.
 +
 
 +
Uveďme príklad: V prechádzajúcom príklade hľadajme číslo x=39
 +
 
 +
Na začiatku máme:
 +
<source lang="c">
 +
i=0
 +
j=10
 +
</source>
 +
Vypočítame m1, m2
 +
<source lang="c">
 +
m1=( i*2 + j ) / 3 = (0+10)/3 = 3
 +
m2=( i + j*2 ) / 3 = (0+20)/3 = 6
 +
</source>
 +
{| class="wikitable" border=1 cellpadding=5
 +
|+pole=
 +
|- style="color:green;background-color:#DADADA"
 +
|0 ||1 ||2 ||m1=3 ||4 ||5 ||m2=6 ||7 ||8 ||9 ||10
 +
|-
 +
|style="background-color:gray" |1
 +
|style="background-color:gray" |2
 +
|style="background-color:gray" |6
 +
|style="font-weight:800" |18
 +
|style="background-color:gray" |20
 +
|style="background-color:gray"| 23
 +
|style="font-weight:800" |29
 +
|style="background-color:yellow"|32
 +
|style="background-color:yellow"|34
 +
|style="background-color:yellow"|39
 +
|style="background-color:yellow"|43
 +
|}
 +
 
 +
Teraz hľadáme v tretej tretine poľa:
 +
<source lang="c">
 +
i=m2+1=7
 +
j=10
 +
</source>
 +
Vypočítame m1, m2
 +
<source lang="c">
 +
m1=( i*2 + j ) / 3 = (14+10)/3 =8
 +
m2=( i + j*2 ) / 3 = (7+20)/3 = 9
 +
</source>
 +
 
 +
{| class="wikitable" border=1 cellpadding=5
 +
|+pole=
 +
|- style="color:green;background-color:#DADADA"
 +
|0 ||1 ||2 ||3 ||4 ||5 ||6 ||7 ||m1=8 ||m2=9 ||10
 +
|-
 +
|style="background-color:gray" |1
 +
|style="background-color:gray" |2
 +
|style="background-color:gray" |6
 +
|style="background-color:gray" |18
 +
|style="background-color:gray" |20
 +
|style="background-color:gray"| 23
 +
|style="background-color:gray" |29
 +
|style="background-color:gray"|32
 +
|style="font-weight:800"|34
 +
|style="font-weight:800"|39
 +
|style="background-color:gray"|43
 +
|}
 +
 
 +
Platí, že x=pole[m2]. Výsledkom bude teda hodnota m2 (index nájdeného prvku v poli)
 +
===Ternárne vyhľadávanie - zdrojový kód v C===
 +
<properties>
 +
Názov funkcie=hladajTernarne
 +
Návratová hodnota=index nájdeného prvku (-1 pri neúspechu)
 +
Parametre=pole prvkov - pole<br/>rozmer poľa - n<br/>hľadaný prvok - x
 +
Zložitosť algoritmu=O(Log n)
 +
</properties>
 +
 
 +
<source lang="c">
 +
int hladajTernarne(int pole[],int i,int j,int x) {
 +
  int m1,m2;
 +
  m1=( i*2 + j ) / 3;
 +
  m2=( i + j*2 ) / 3;
 +
  if(x==pole[m1])
 +
    return m1;
 +
  if(x==pole[m2]) 
 +
    return m2;
 +
  if(i>j) return -1; // prvok sa nenašiel 
 +
  if(x<pole[m1]) // hľadaj v prvej tretine
 +
    return(hladajTernarne(pole, i,m1-1,x));
 +
  if(x>pole[m2])  // hľadaj v druhej tretine
 +
    return(hladajTernarne(pole, m2+1,j,x));
 +
  else  // hľadaj v tretej tretine
 +
    return(hladajTernarne(pole, m1+1,m2-1,x));
 +
}
 +
</source>
 +
 
 +
===Porovnanie binárneho a ternárneho vyhľadávania===
 +
;Provnávané varianty:rekurzívne verzie funkcií
 +
;Spôsov porovnávania: Veľkosť poľa v ktorom hľadáme - n (os x grafu)<br/>
 +
:Počet hľadaných čísel - 1000<br/>
 +
:Počet opakovaní každého hľadania - 1000
 +
 
 +
<pLines ymin=0 axiscolor=888888 cubic angle=90 plots legend xtitle=pocet_cisel ytitle=cas_[s]>
 +
,binarne,ternarne
 +
1 000, 2.115, 2.094
 +
5 000, 2.537, 2.513
 +
10 000, 2.674, 2.622
 +
50 000, 3.028, 3.005
 +
100 000, 3.252, 3.032
 +
500 000, 3.642, 3.358
 +
1 000 000, 3.719, 3.471
 +
5 000 000, 4.129, 3.771
 +
10 000 000, 4.410, 3.963
 +
50 000 000, 5.679, 4.304
 +
100 000 000, 5.806, 5.248
 +
</pLines>
  
 
=Vyhľadávanie v rekurzívnych štruktúrach=
 
=Vyhľadávanie v rekurzívnych štruktúrach=
−
==Vyhľadývanie v binárnych stromoch==
+
Ďalším špeciálnym typom vyhľadávania je vyhľadávanie v rekurzívne definovaných štruktúrach. Medzi tieto štruktúry patria [[Strom_Dátová štruktúra|stromy]], konkrétne [[Binárny strom]] alebo [[B-strom]]. V týchto štruktúrach sa nedá implementovať lineárne vyhľadávanie ani binárne (resp. ternárane) vyhľadávanie, pretože samotná štruktúra takéhoto dátového typu to nedovoľuje.
 +
==Vyhľadávanie v binárnych stromoch==
 +
Najjednoduchšia forma stromu je binárny strom. Binárny strom je stromová dátová štruktúra, v ktorej každý uzol má najviac dvoch potomkov. Binárny strom sa skladá z
 +
# koreňového uzla
 +
# ľavý a pravý podstrom.
 +
#*Oba podstromy sú taktiež binárne stromy.
 +
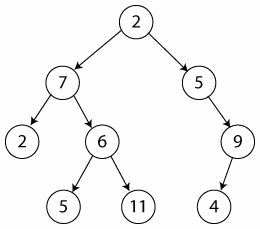
[[Súbor:binStrom.png|frame|right|Binárny strom]]
 +
Uzly na najnižšej úrovni stromu (2, 5, 11, 4) sa nazývajú ''listy''.
 +
Vlastnosťou binárneho stromu je to, že údaje v ňom sú vždy usporiadané nasledovným spôsobom:
 +
* naľavo od uzla sú tie prvky, ktoré majú hodnotu menšiu ako tohoto uzla
 +
* napravo od uzla sú tie prvky, ktoré majú hodnotu väčšiu ako tohoto uzla
 +
 
 +
Pri tomto predpoklade môžeme sformulovať vyhľadávací algoritmus pre binárne stromy:
 +
 
 +
Budeme hľadať v binárnom strome, ktorý si označme ''bstrom''. Tento každý uzol stromu môže mať žiadneho, jedného alebo dvoch potomkov. Potomkov budeme značiť ''ľavý'' a ''pravý''. V strome ''bstrom'' budeme hľadať prvok ''x''.
 +
 
 +
#Označ si koreň stromu v ktorom budeme hľadať ako ''uzol''.
 +
#Porovnaj hodnotu uzla ''uzol'' s hľadaným prvkom ''x''.
 +
#Ak sa tieto hodnoty zhodujú - koniec. Našli sme prvok ''x''.
 +
#Ak aktuálny ''uzol'' nemá potomkov, tak koniec - Nenašli sme prvok ''x''.
 +
#Ak je hodnota ''x'' menšia ako hodnota uzla ''uzol'', tak označ si ako ''uzol'' potomka ''ľavý''. Choď na krok 1.
 +
#Ak je hodnota ''x'' menšia ako hodnota uzla ''uzol'', tak označ si ako ''uzol'' potomka ''pravý''. Choď na krok 1.
 +
 
 +
Pseudokód algoritmu vyhľadávania:
 +
<source lang="text">
 +
hľadaj(strom, x)
 +
uzol <- vrhol stromu strom
 +
ak je uzol list
 +
  koniec - x sme nenašli
 +
ak je hodnota uzla == x tak
 +
  koniec - vráť hodnotu x
 +
ak je hodnota uzla < x tak
 +
  hľadaj(uzol->lavy,x)
 +
ak je hodnota uzla > x tak
 +
  hľadaj(uzol->pravy,x)
 +
</source>
 +
značenie uzol->lavy, resp. uzol->pravy má význam, že ďalej budeme pracovať len s ľavou, resp. pravou časťou binárneho stromu.
 +
 
 +
===Implementácia v jazyku C===
 +
Definícia binárneho stromu je v kapitole [[Binárny strom]]. Pre správne pochopenie nasledujúcej časti je potrebné vedieť pracovať s binárnym stromom.
 +
 
 +
 
 +
Definujme dátovú štruktúru binárny strom:
 +
<source lang="c">
 +
struct TUzol
 +
{  int data;
 +
TUzol *lavy,*pravy;
 +
};
 +
</source>
 +
 
 +
 
 +
<properties>
 +
Názov funkcie=hladajRekurzivneStrom
 +
Návratová hodnota=smerník na nájdený prvok (v prípade neúspechu NULL)
 +
Parametre=binárny strom - strom<br/>hľadaný prvok - x
 +
Zložitosť algoritmu=O(n)
 +
</properties>
 +
 
 +
<source lang="c">
 +
TUzol* hladajRekurzivneStrom(TUzol *s, int x)
 +
{
 +
  if(s==NULL) return NULL; 
 +
  if(s->data == x ) return s;
 +
  if(x < s->data) return hladajRekurzivneStrom(s->lavy);
 +
  if(x > s->data) return hladajRekurzivneStrom(s->pravy);
 +
 
 +
}
 +
</source>
 +
 
  
−
=HASH funckie=
+
=Odkazy=
 +
* http://en.wikipedia.org/wiki/Linear_search
 +
* http://en.wikipedia.org/wiki/Binary_search
 +
* http://en.wikipedia.org/wiki/Ternary_search
 +
* http://www.dcc.uchile.cl/~rbaeza/handbook/search_a.html
 +
* http://www.cs.auckland.ac.nz/software/AlgAnim/searching.html
 +
* http://www.cs.auckland.ac.nz/software/AlgAnim/trees.html

Aktuálna revízia z 21:15, 16. august 2010

Imbox draft.png
 Toto je projekt, na ktorom sa ešte stále pracuje!!

Aj keď sú v tomto dokumente použiteľné informácie, ešte nie je dokončený. Svoje návrhy môžete vyjadriť v diskusii o tejto stránke.

Algoritmy a programovanie

Dátový typ

Štruktúry

Rekurzia

Algoritmy vyhľadávania

Algoritmy triedenia

Lineárny zoznam

Binárny strom

Numerické algoritmy

Grafové algoritmy

Practice.png
 Praktické príklady

Riešené príklady k tejto téme sú na stránke Vyhľadávanie (riešené príklady)

Vyhľadávanie

Vyhľadávanie je základnou úlohou pri práci s väčším objemom dát. Podľa povahy dát (zložitosti, usporiadania, veľkosti) volíme vhodný algoritmus vyhľadávania. Algortimy vyhľadávanie môžeme rozdeliť do niekoľko skupín:

  1. Sekvenčné vyhľadávanie
  2. Vyhľadávanie v usporiadaných zoznamoch (resp. poliach)
  3. Vyhľadávanie v rekurzívnych štruktúrach


Sekvenčné vyhľadávanie

Jednoduché sekvenčné vyhľadávanie

Princíp tohto vyhľadávania je jednoduchý. Majme pole údajov o dĺžke n, v ktorých budeme hľadať údaj x. Pod pojmom údaj si môžeme ptredstaviť ľubovoľný dátový typ (celé číslo, reálne číslo, štruktúru, smerník na nejaký dátový typ). Princíp: postupne prechádzame pole od indexu 0 až po index n-1. V prípade, ak zistíme zhodu hľadaného prvku s prvkom v poli, tak funkciu ukončíme s úspechom, v opačnom prípade skončíme s výsledkom "prvok sa nenašiel"

Dohodnuté návratové hodnoty funkcie:

Vyhľadávacia funkcia bude vracať index prvku, ktorý je zhodný s hľadaným prvkom. V prípade neúspechu (hľadaný prvok sa v poli nevyskytuje) vráti funkcia hodnotu -1.

Názov funkcie

hladajSekvencne

Návratová hodnota

index nájdeného prvku (-1 pri neúspechu)

Parametre

pole prvkov - pole
rozmer poľa - n
hľadaný prvok - x

Zložitosť algoritmu

O(n)


1 int hladajSekvencne(int *pole,int dlzka,int x)
2 {  int i=0;
3 	while( (i<dlzka) && (pole[i]!=x) )
4 		 i++;
5     if(i<dlzka)  return i;
6 	else return -1;
7 }

Analýza riešenia: Algoritmus je vhodný pre vyhľadávanie údajov v dátovej štruktúre jednorozmerné pole. Údaje v tomto poli môžu byť neusporiadané. Podmienka i<dlzka zaručí, že sa bude prehľadávať len v rozsahu poľa pole. Vždy sa začína na indexe i=0; tento index sa postupne zvyšuje (i++), pokiaľ nenarazíme na hľadaný prvok (pole[i]!=x). Podmienka na riadku 5 je tam pre kontrolu prípadu, keď sme prešli celé pole a hľadaný prvok sme nenašli.

Nevýhoda: každý cyklus sa vykonávajú 2 porovnania: i<dlzka a pole[i]!=x

Jednoduché sekvenčné vyhľadávanie s nárazníkom

V predchádzajúcom prípade sa v každom cykle robili 2 porovnania. Určitými úpravami dokážeme tieto porovnania znížiť len na 1 porovnanie. Bude to však chcieť drobnú úpravu poľa, v ktorom budeme vyhľadávať. Pole si upravíme tak, že hľadaný prvok sa tam bude vždy vyskytovať. Skutočná veľkosť poľa pole musí byť teda o jednu položku väčšia ako je počet prvkov v poli. Iba po splnení tejto podmienky môžeme urobiť priradenie, ako je ukázané v riadku 3. Toto priradenie nazveme nárazník.

Názov funkcie

hladajSekvencneN

Návratová hodnota

index nájdeného prvku (-1 pri neúspechu)

Parametre

pole prvkov - pole
rozmer poľa - n
hľadaný prvok - x

Zložitosť algoritmu

O(n)


 1 int hladajSekvencneN(int *pole, int n, int x)
 2 {
 3   pole[n] = x; // musi byt na to vyhradene miesto!
 4   int i = 0;
 5   while (pole[i] != x) 
 6     i++;
 7   if (i < n) 
 8     return i;
 9   else
10     return -1;
11 }

Analýza riešenia: Algoritmus je vhodný pre vyhľadávanie údajov v dátovej štruktúre jednorozmerné pole. Údaje v tomto poli môžu byť neusporiadané. Priradenie pole[n] = x dovoľuje vynechať kontrolu i<dlzka (funkcia hladajSekvencne). Vieme, že prvok v poli vždy nájdeme, preto stačí na konci urobiť porovnanie (riadok 7), či sme prvok x našli na pozícii menšej ako n (v rozsahu poľa). Ak áno, vrátime hodnotu premennej i, čo je index nájdeného prvku, ak sme hľadaný prvok našli na pozícii n, vrátime hodnotu -1, pretože na pozícii n je náš nárazník.

Poznámka: Touto úpravou sme vylepšili čas, vyhľadávania, ale nie zložitosť algoritmu.

Nasledujúci obrázok ukazuje porovanie časov vyhľadávania doteraz spomínaných algorimnov pri opakovanom vyhľadávaní vo veľkých (cca 1 000 000 položiek) poliach. <pLines ymin=0 axiscolor=888888 cubic angle=90 plots legend xtitle=pocet_cisel ytitle=cas> ,hladajSekvencne,hladajSekvencneN 10 000, 0.016, 0.015 100 000, 0.235, 0.125 200 000, 0.859, 0.813 300 000, 1.281, 1.234 500 000, 2.156, 2.063 700 000, 3.031, 2.891 1 000 000, 4.328, 4.141 2 000 000, 8.656, 8.375 5 000 000, 21.531, 20.657 10 000 000, 42.422, 41.235 </pLines>

Vyhľadávanie v usporiadaných zoznamoch

Zložitosť O(n) pre algorimy lineárneho, resp. sekvenčného vyhľadávania dokážeme znížiť, ak sú údaje v ktorých budeme vyhľadávať usporiadané. V tomto prípade nemusíme pole prvkov v ktorom hľadáme prechádzať celé (od indexu 0 až po n-1), ale stačí si skontrolovať položky len na určitých miestach.

Binárne vyhľadávanie

Predpoklad správneho vyhľadávania je, že prvku sú v poli usporiadané. Postup vyhľadávania:

Použité premenné
  • pole - jednorozmerné pole, v ktorom budeme vyhľadávať
  • x - prvok, ktorý hľadáme
  • n - veľkosť pola pole.
  • lavy, pravy - rozsah poľa, (začiatok , koniec) kde budeme hľadať.


  1. Rozdeľ pole na 2 polovice. Index stredného prvku vypočítaš ako:
    • stred=(lavy+pravy)/2
  2. Ak platí lavy>pravy, tak koniec, prvok sa nenašiel.
  3. Zober prvok v strede poľa (na indexe stred) a porovnaj ho s hľadaným prvkom x
  4. Ak sa x zhoduje so stredným prvkom - koniec. Výsledok je index tohto prvku
  5. V opačnom prípade
    • Ak je x väčšie ako stredný prvok, tak hľadaj v pravej časti poľa
      • lavy=stred+1, pravy zostava nezmenený (choď na krok 1)
    • Ak je x menšie ako stredný prvok, tak hľadaj v ľavej časti poľa
      • lavy=zostava nezmenený, pravy = stred-1 (choď na krok 1)

Ukážme si konkrétny príklad (šedé políčka predstavujú indexy poľa, biele sú prvky poľa): 

 x=18
 n=10
pole=
0 1 2 3 4 5 6 7 8 9 10
1 2 6 18 20 23 29 32 34 39 43

Pre implementáciu algoritmu binárneho vyhľadávania si musíme vypočítať hodnoty ľavého a pravého indexu poľa, v ktorom hľadáme. Na začiatok je to jednoduché: 

 lavy=0
 pravy=n-1
  • Porovnajme hľadaný prvok x=18 so stredným prvkom:
 stred=(lavy+pravy)/2
 stred=5
pole=
0 1 2 3 4 5 6 7 8 9 10
1 2 6 18 20 23 29 32 34 39 43
  • pole[5] != x (23 != 18 )
    • platí že x<23 (resp. x<pole[stred])
    • budeme vyhľadávať vľavo (žltá časť)
      • lavy zostane nezmeneny (0)
      • pravy=stred - 1 (4)
  • Porovnajme hľadaný prvok x=18 so stredným prvkom:
 stred=(lavy+pravy)/2 = (0+4)/2=2
 stred=2
pole=
0 1 2 3 4 5 6 7 8 9 10
1 2 6 18 20 23 29 32 34 39 43
  • pole[2] != x (6 != 18 )
    • platí že x>6 (resp. x>pole[stred])
    • budeme vyhľadávať vpravo (žltá časť)
      • lavy = stred + 1 (3)
      • pravy zostane nezmeneny (4)
  • Porovnajme hľadaný prvok x=18 so stredným prvkom:
 stred=(lavy+pravy)/2 = (3+4)/2=3
 stred=3
  • pole[3] == x (18 = 18 )
  • Stredný prvok je zhodný s hľadaným
  • Algoritmus končí
    • Výsledok je index nájdeného prvku, teda stred. V našom príklade je to 3.

Binárne vyhľadávanie - zdrojový kód v jazyku C

Názov funkcie

hladajBinarne
hladajBinarneR

Návratová hodnota

index nájdeného prvku (-1 pri neúspechu)

Parametre

pole prvkov - pole
rozmer poľa - n
hľadaný prvok - x

Zložitosť algoritmu

O(Log(n))


Keďže samotné definícia binárneho vyhľadávania je rekurzívna, uvádzame aj rekurzívnu verziu funkcie.


Iteračná verzia 

int hladajBinarne(int *pole,int dlzka, int x)
{	int najdene=0;
int lavy = 0, pravy = dlzka - 1, stred;
while ( (lavy <= pravy) && (najdene==0) )
{
   stred = (lavy + pravy) / 2;
   if (pole[stred] == x) 
	 najdene=1;
   else 
  	  if (pole[stred] < x) 
	     lavy = stred + 1;
	   else 
 	     pravy=stred - 1;
}
if(najdene==1)
	return stred;
else
	return -1;
}

Rekurzívna verzia 

int hladajBinarneR(int *pole,int lavy, int pravy, int x)
{   if(lavy>pravy)
		return -1;
	else
	{	
		int stred=(lavy+pravy)/2;
		if(pole[stred]==x)
		  return stred;
		else
		{   if( x<pole[stred] )
			return hladajB(pole,lavy,stred-1,x);
		   else
			return hladajB(pole,stred+1,pravy,x);
		}
	}
}

Ternárne vyhľadávanie

Predpoklad správneho vyhľadávania je, že prvku sú v poli usporiadané. Postup vyhľadávania je podobný ako pri binárnom vyhľadávaním abšak pole nerozdelíme na polovicu ale na tretiny.

Použité premenné
  • pole - jednorozmerné pole, v ktorom budeme vyhľadávať
  • x - prvok, ktorý hľadáme
  • n - veľkosť pola pole.
  • i, j - rozsah poľa, (začiatok , koniec) kde budeme hľadať.
  • m1 - index prvku v prvej tretine
  • m2 - index prvku v druhej tretine


  1. Rozdeľ pole na tretiny
    1. m1=( i*2 + j ) / 3;
    2. m2=( i + j*2 ) / 3;
  2. Porovnaj, či sa hľadaný prvok zhoduje z prvkom na indexe m1, ak áno, tak koniec. Výsledok je index m1
  3. Porovnaj, či sa hľadaný prvok zhoduje z prvkom na indexe m2, ak áno, tak koniec. Výsledok je index m2
  4. Ak platí i>j, skonči, prvok x sa v poli nenachádza.
  5. Ak je hľadaný prvok menší ako prvok pole[m1], tak hľadaj v prvej tretine poľa
    • i zostáva nezmenené , j=m1-1. Choď na krok 1.
  6. Ak je hľadaný prvok väčší ako prvok pole[m2], tak hľadaj v tretej tretine poľa
    • i = m2+1 , j zostáva nezmenené. Choď na krok 1.
  7. inak hľadaj v druhej tretine poľa
    • i = m1+1 , j=m2-+. Choď na krok 1.

Uveďme príklad: V prechádzajúcom príklade hľadajme číslo x=39

Na začiatku máme: 

 i=0
 j=10

Vypočítame m1, m2 

 m1=( i*2 + j ) / 3 = (0+10)/3 = 3
 m2=( i + j*2 ) / 3 = (0+20)/3 = 6
pole=
0 1 2 m1=3 4 5 m2=6 7 8 9 10
1 2 6 18 20 23 29 32 34 39 43

Teraz hľadáme v tretej tretine poľa: 

 i=m2+1=7
 j=10

Vypočítame m1, m2 

 m1=( i*2 + j ) / 3 = (14+10)/3 =8
 m2=( i + j*2 ) / 3 = (7+20)/3 = 9
pole=
0 1 2 3 4 5 6 7 m1=8 m2=9 10
1 2 6 18 20 23 29 32 34 39 43

Platí, že x=pole[m2]. Výsledkom bude teda hodnota m2 (index nájdeného prvku v poli)

Ternárne vyhľadávanie - zdrojový kód v C

Názov funkcie

hladajTernarne

Návratová hodnota

index nájdeného prvku (-1 pri neúspechu)

Parametre

pole prvkov - pole
rozmer poľa - n
hľadaný prvok - x

Zložitosť algoritmu

O(Log n)


int hladajTernarne(int pole[],int i,int j,int x) {
  int m1,m2;
  m1=( i*2 + j ) / 3;
  m2=( i + j*2 ) / 3;
  if(x==pole[m1])
    return m1;
  if(x==pole[m2])   
    return m2;
  if(i>j) return -1; // prvok sa nenašiel  
  if(x<pole[m1]) // hľadaj v prvej tretine
    return(hladajTernarne(pole, i,m1-1,x));
  if(x>pole[m2])  // hľadaj v druhej tretine
    return(hladajTernarne(pole, m2+1,j,x));
  else   // hľadaj v tretej tretine
    return(hladajTernarne(pole, m1+1,m2-1,x));
}

Porovnanie binárneho a ternárneho vyhľadávania

Provnávané varianty
rekurzívne verzie funkcií
Spôsov porovnávania
Veľkosť poľa v ktorom hľadáme - n (os x grafu)
Počet hľadaných čísel - 1000
Počet opakovaní každého hľadania - 1000

<pLines ymin=0 axiscolor=888888 cubic angle=90 plots legend xtitle=pocet_cisel ytitle=cas_[s]> ,binarne,ternarne 1 000, 2.115, 2.094 5 000, 2.537, 2.513 10 000, 2.674, 2.622 50 000, 3.028, 3.005 100 000, 3.252, 3.032 500 000, 3.642, 3.358 1 000 000, 3.719, 3.471 5 000 000, 4.129, 3.771 10 000 000, 4.410, 3.963 50 000 000, 5.679, 4.304 100 000 000, 5.806, 5.248 </pLines>

Vyhľadávanie v rekurzívnych štruktúrach

Ďalším špeciálnym typom vyhľadávania je vyhľadávanie v rekurzívne definovaných štruktúrach. Medzi tieto štruktúry patria stromy, konkrétne Binárny strom alebo B-strom. V týchto štruktúrach sa nedá implementovať lineárne vyhľadávanie ani binárne (resp. ternárane) vyhľadávanie, pretože samotná štruktúra takéhoto dátového typu to nedovoľuje.

Vyhľadávanie v binárnych stromoch

Najjednoduchšia forma stromu je binárny strom. Binárny strom je stromová dátová štruktúra, v ktorej každý uzol má najviac dvoch potomkov. Binárny strom sa skladá z

  1. koreňového uzla
  2. ľavý a pravý podstrom.
    • Oba podstromy sú taktiež binárne stromy.
Binárny strom

Uzly na najnižšej úrovni stromu (2, 5, 11, 4) sa nazývajú listy. Vlastnosťou binárneho stromu je to, že údaje v ňom sú vždy usporiadané nasledovným spôsobom:

  • naľavo od uzla sú tie prvky, ktoré majú hodnotu menšiu ako tohoto uzla
  • napravo od uzla sú tie prvky, ktoré majú hodnotu väčšiu ako tohoto uzla

Pri tomto predpoklade môžeme sformulovať vyhľadávací algoritmus pre binárne stromy:

Budeme hľadať v binárnom strome, ktorý si označme bstrom. Tento každý uzol stromu môže mať žiadneho, jedného alebo dvoch potomkov. Potomkov budeme značiť ľavý a pravý. V strome bstrom budeme hľadať prvok x.

  1. Označ si koreň stromu v ktorom budeme hľadať ako uzol.
  2. Porovnaj hodnotu uzla uzol s hľadaným prvkom x.
  3. Ak sa tieto hodnoty zhodujú - koniec. Našli sme prvok x.
  4. Ak aktuálny uzol nemá potomkov, tak koniec - Nenašli sme prvok x.
  5. Ak je hodnota x menšia ako hodnota uzla uzol, tak označ si ako uzol potomka ľavý. Choď na krok 1.
  6. Ak je hodnota x menšia ako hodnota uzla uzol, tak označ si ako uzol potomka pravý. Choď na krok 1.

Pseudokód algoritmu vyhľadávania: 

hľadaj(strom, x)
uzol <- vrhol stromu strom
ak je uzol list
  koniec - x sme nenašli
ak je hodnota uzla == x tak 
  koniec - vráť hodnotu x
ak je hodnota uzla < x tak
  hľadaj(uzol->lavy,x)
ak je hodnota uzla > x tak
  hľadaj(uzol->pravy,x)

značenie uzol->lavy, resp. uzol->pravy má význam, že ďalej budeme pracovať len s ľavou, resp. pravou časťou binárneho stromu.

Implementácia v jazyku C

Definícia binárneho stromu je v kapitole Binárny strom. Pre správne pochopenie nasledujúcej časti je potrebné vedieť pracovať s binárnym stromom.


Definujme dátovú štruktúru binárny strom: 

struct TUzol
{   int data;
	 TUzol *lavy,*pravy;
};


Názov funkcie

hladajRekurzivneStrom

Návratová hodnota

smerník na nájdený prvok (v prípade neúspechu NULL)

Parametre

binárny strom - strom
hľadaný prvok - x

Zložitosť algoritmu

O(n)


TUzol* hladajRekurzivneStrom(TUzol *s, int x)
{ 
  if(s==NULL) return NULL;   
  if(s->data == x ) return s;
  if(x < s->data) return hladajRekurzivneStrom(s->lavy);
  if(x > s->data) return hladajRekurzivneStrom(s->pravy);

}


Odkazy

Zdroj: „http://www.kiwiki.info/index.php?title=Algoritmy_vyhľadávania&oldid=6647“