Triedenie výberom

Algoritmy a programovanie

---

Dátový typ

Štruktúry

Rekurzia

Algoritmy vyhľadávania

Algoritmy triedenia

>Triedenie výmenou
>Triedenie vkladaním
>Triedenie zlučovaním
>Triedenie delením
>Triedenie výberom
>Triedenie - ostatné princípy

Lineárny zoznam

Binárny strom

Numerické algoritmy

Grafové algoritmy

Heap Sort

Prehľad

Heap Sort je triediaci algoritmus, ktorý podobne ako Selection sort, rozeľuje pole na zotriedenú a nezotriedenú časť, pričom nezotriedená časť predstavuje dátovú štruktúru binárna hromada. Celé triedenie spočíva v tom, že si zo vstupného poľa vytvoríme binárnu hromadu a následne postupným vyberaním a mazaním všetkých jej prvkov toto pole utriedime.

Hromada, ktorú využíva algoritmus Heap Sort, musí spĺňať nasledovné podmienky (ak indexujeme pole od 0):

1. Vrchol hromady (koreň) je vždy prvý prvok v poli (v našom prípade prvok na 0-tej pozícii).

2. Pre ľubovoľný prvok (uzol), uložený na indexe [math]i[/math] z intervalu [math] \langle 0 \ ; \ \text{dĺžka} - 1 \rangle [/math], platia nasledovné rovnice:

[math] \begin{align} \text{ľavý potomok} &= 2i + 1 && (1) \\ \text{pravý potomok} &= 2i + 2 && (2) \\ \text{rodič} &= \left \lfloor \frac{i - 1}{2} \right \rfloor \quad (\text {okrem} \ i = 0) && (3) \end{align} [/math]

3. Každý prvok (uzol) v hromade musí mať väčšiu, alebo rovnakú hodnotu ako jeho potomkovia (vlastnosť MAX HEAP - ak triedime pole vzostupne, v opačnom prípade by sme použili MIN HEAP).

Algoritmus Heapify

Vizualizácia algoritmu Heapify: Index i je iteračná premenná (pozri pseudokód). Ľavý a pravý potomok i-teho prvku je označený ako ĽP a PP. Prvky zafarbené na modro vyjadrujú pravú podhromadu i-teho prvku a prvky zafarbené na zeleno vyjadrujú ľavú podhromadu i-teho prvku. Chronlogický postup algoritmu je znázornený číslicami 1 až 3.

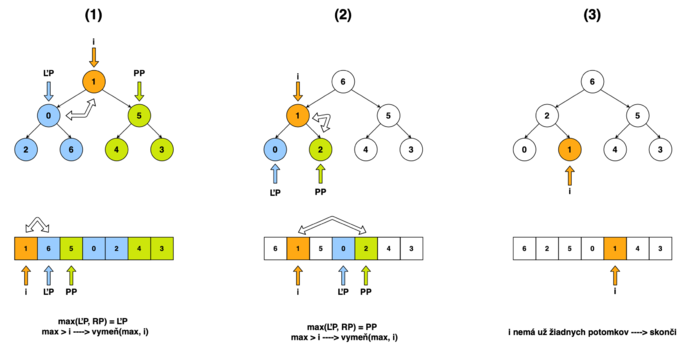
Heapify je kľúčovým podprogramom triediaceho algoritmu Heap Sort, vďaka ktorému vieme efektíve zabezpečiť procedúry: vytvorenie hromady z poľa a zmazanie hromady.

Princíp algoritmu Heapify spočíva v tom, že ak máme i-ty prvok v poli (v kompletnom binárnom strome), ktorého potomkovia tvoria dve samostatné podhromady, potom tieto dve podhromady preusporiadame do jednej hromady, pričom i-ty prvok bude jej vrcholom.

Vlastnosti algoritmu

• dátová štruktúra: hromada (reprezentovaná ako: pole)
• časová zložitosť: lineárna [math]O(n)[/math]
• priestorová zložitosť: konštantná [math]O(1)[/math] pri iteračnej verzii, [math]O(log(n))[/math] pri rekurzívnej verzii

Základné časti algoritmu

1. Určenie potomka i-teho prvku s maximálnou hodnotou.
2. Porovnanie hodnoty maximálneho potomka s hodnotou rodiča (i-tym prvkom).
3. Ak je hodnota maximálneho potomka väčšia ako hodnota rodiča, tak výmena potomka a rodiča.
4. Ak nastane výmena, skontrolovanie ovplyvneného potomka (podhromady).

Slovný opis algoritmu

Na vstupe prijmeme pole a index i, v ktorom chceme vytvoriť hromadu (Max Heap). Musí byť splnená podmienka, že oba potomkovia i-teho prvku tvoria dve samostatné podhromady. Najskôr skontrolujeme, či prvok na indexe i má nejakých potomkov (využijeme rovnice (1) a (2) z časti "Prehľad"). Ak nemá žiadnych potomkov, funkcia skončí, pretože i predstavuje vrchol jednoprvkovej hromady. Ak má práve jedného potomka, tento potomok je zároveň aj jeho maximálnym potomkom. Ak má práve dvoch potomkov, tak porovnáme ich hodnoty a vyberieme z nich maximálneho potomka. Následne skontrolujeme veľkosť maximálneho potomka a jeho rodiča (prvok na indexe i). Ak je rodič väčší, funkcia skončí, pretože želaná hromada už je utvorená. Ak nie, vymeníme rodiča a maximálneho potomka. Ak nastala výmena, musíme skontrolovať ovplyvnenú podhromadu, tj. zopakovať tento sled krokov pre podhromadu, ktorej vrchol bude v maximálnom potomkovi i-teho prvku.

Z hľadiska implementácie môžeme vytvoriť iteračnú aj rekurzívnu verziu.

Pseudokód

Iteračná verziaRekurzívna verzia

Nech funkcia Heapify má nasledovný prototyp: Heapify(pole[], dlzka, i)

1. Je 2 * i + 1 < dlzka ? Ak áno, pokračuj krokom 1.1., inak skonči.

1.1. Nech: lavy = 2 * i + 1

1.2. Nech: pravy = 2 * i + 2

1.3. Je pravy < dlzka a zároveň pole[pravy] > pole[lavy] ?

Ak áno:

1.3.1. Nech: max = pravy

Ak nie:

1.3.1. Nech: max = lavy

1.4. Je pole[max] > pole[i] ?

Ak áno:

1.4.1. Vymeň: pole[max] a pole[i]

1.4.2. i = max

Ak nie:

1.4.1 Skonči.

1.5. Skoč na krok 1.

Nech funkcia Heapify má nasledovný prototyp: Heapify(pole[], dlzka, i)

1. Nech: lavy = 2 * i + 1

2. Nech: pravy = 2 * i + 2

3. Nech: max = i

4. Je lavy < dlzka a zároveň pole[lavy] > pole[max] ?

Ak áno:

4.1. Nech: max = lavy

Ak nie:

4.1. Pokračuj krokom 5.

5. Je pravy < dlzka a zároveň pole[pravy] > pole[max] ?

Ak áno:

5.1. Nech: max = pravy

Ak nie:

5.1. Pokračuj krokom 6.

6. Je pole[max] > pole[i] ?

Ak áno:

6.1. Vymeň: pole[i] a pole[max]

6.2. Rekurzívne zavolaj: Heapify(pole[], dlzka, max)

Ak nie:

6.1. Skonči volanie.

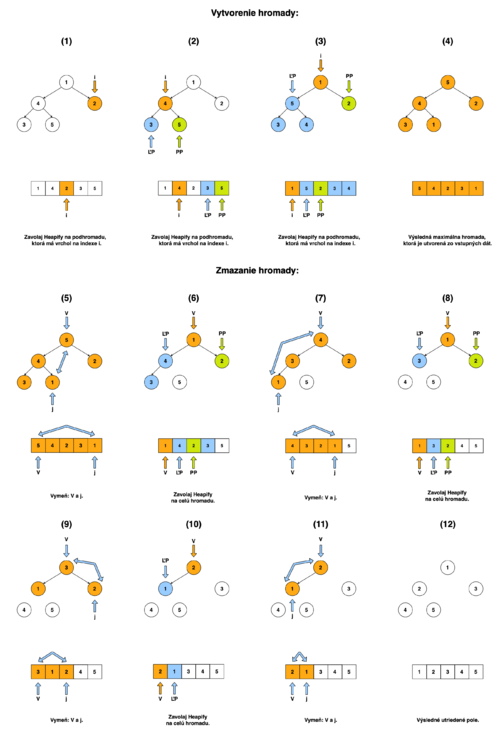
Algoritmus Heap Sort

Heap Sort pri triedení vykonáva dve základné úlohy: Vytvorenie maximálnej binárnej hromady zo vstupného poľa a postupné mazanie jednotlivých prvkov z hromady. Pri oboch procedúrach využíva algoritmus Heapify.

Vlastnosti algoritmu

• vhodný pre dátové štruktúry: pole
• časová náročnosť: vždy linearitmická [math] O(n\log(n)) [/math], vďaka ktorej dokáže efektívne triediť veľmi veľké polia

Vizualizácia priebehu algoritmu Heap Sort: Algoritus je znázornený pomocou poľa, ktoré triedime a binárnej hromady, ktorú dané pole reprezentuje. Indexy i a j sú sú iteračné premenné (pozri pseudokód). Indexy ľavého a pravého potomka i-teho prvku sú označené ako ĽP a PP. Vrchol celej hromady je označený ako V. Prvky zafarbené na modro vyjadrujú pravú podhromadu i-teho prvku a prvky zafarbené na zeleno vyjadrujú ľavú pohromadu i-teho prvku. Nevyfarbené prvky vyjadrujú prvky, ktoré boli zmazané. Chronologický priebeh je označený číslicami 1 až 12.

• priestorová náročnosť: konštantná [math]O(1)[/math] pri iteračnej verzii, logaritmická [math]O(\log(n))[/math] pri rekurzívnej verzii.
• druh triedenia: triedenie výberom (komparačný algoritmus)
• stabilita triedenia: nestabilný
• miesto triedenia: vnútorné triedenie

Základné časti algoritmu

1. Vytvorenie binárnej hromady z poľa.
2. Zmazanie binárnej hromady.

Slovný opis

Vytvorenie hromady

Pri vytváraní hromady využijeme algoritmus Heapify, pričom hromadu vytvoríme spôsobom zospodu na vrch.

Najskôr si určíme rodiča posledného potomka. Využijeme rovnicu (3) z časti "Prehľad", ktorú si jemne upravíme:

[math] \text{posledný rodič:} \ \ i = \left \lfloor \frac{\text{posledný index } - \ 1}{2} \right \rfloor = \left \lfloor\frac{\text{dĺžka } - \ 2}{2} \right \rfloor = \left \lfloor \frac{\text{dĺžka}}{2}\right \rfloor - 1 [/math]

Následne zavoláme Heapify na podhromadu s vrcholom na indexe i. Potom postupne zmenšujeme index i o 1 a opakovane naňho voláme Heapify až do chvíle, kým neprídeme na začiatok poľa. Touto procedúrou preusporiadavame spodné jednoprvkové podhromady do 3-prvkových podhromád, tie do 7-prvkových podhromád ... až kým nedostaneme jednu N-prvkovú hromadu, kde N je počet prvkov v poli. Schematicky by sme to mohli napísať takto:

[math] \text{pre } i \text{ z intervalu } \left \langle \left \lfloor \frac {\text{dĺžka}}{2} \right \rfloor - 1 \quad ; \quad 0 \right \rangle :\ \text{Heapify( pole[], dĺžka, i )}[/math]

Zmazanie hromady

Pri mazaní hromady vykonáme dve operácie. Ako prvé vymeníme prvok na vrchu hromady s koncovým prvkom hromady. Prvok čo je na konci poľa považujeme už za zmazaný, preto veľkosť hromady znížime o 1. Ďalej, aby sme splnili podmienky pre maximálnu binárnu hromadu, zavoláme funkciu Heapify na celú hromadu (vrch hromady je 0-tý prvok v poli). Tento proces opakujeme, pokým v hromade neostanú žiadne prvky.

Poznámka: Pri triediacom algoritme nemusíme mazať celú hromadu, stačí nám, keď v hromade ostane jeden prvok, pretože vtedy bude vstupné pole už utriedené.

Schematicky by sme to mohli zapísať takto:

[math]\text{pre } j \text{ z intervalu } \left \langle \text{dĺžka - 1} \quad ; \quad 0 \right ) : \ \ \text{Vymeň(pole[0], pole[$j$])} \ \ a \ \ \text{Heapify(pole[], dĺžka, 0)} [/math]

Z hľadiska implementácie môžeme vytvoriť iteračnú aj rekurzívnu verziu, čo závisí len od toho, ako je implementovaná funkcia Heapify.

Pseudokód

Nech funkcia Heap Sort má nasledovný prototyp: HeapSort(pole[], dlzka)

1. Nech: i = dlzka / 2 - 1, kde "/" predstavuje celočíslené delenie.

2. Je i >= 0 ? Ak áno, pokračuj krokom 2.1., inak skoč na krok 3.

2.1. Zavolaj funkciu: Heapify(pole[], dlzka, i)

2.2. i = i - 1

2.3. Skoč na krok 2.

3. Nech: j = dlzka - 1

4 Je j > 0 ? Ak áno, pokračuj krokom 4.1, inak skonči.

4.1. Vymeň: pole[0] a pole[j]

4.2. Zavolaj funkciu: Heapify(pole[], j, 0)

4.3. j = j - 1

4.4. Skoč na krok 4.

Implementácia algoritmov Heapify a HeapSort v rôznych programovacích jazykoch

Iteračná CRekurzívna CIteračná C++Rekurzívna C++Iteráčná JavaRekurzívna JavaIteračná Python3Rekurzívna Python3

#include <stdio.h>

void Vymen(int *a, int *b);
void Heapify(int pole[], int dlzka, int index);
void HeapSort(int pole[], int dlzka);

int main()
{
    int pole[]= {10, 5, 2, 9, 8, 7, 1, 3, 4, 0, -1};
    int dlzka = sizeof(pole) / sizeof(pole[0]);

    HeapSort(pole, dlzka);

    for (int i = 0; i < dlzka; ++i)
    {
        printf("%d ", pole[i]);
    }
}


void Vymen(int *a, int *b)
{
    int tmp = *a;
    *a = *b;
    *b = tmp;
}

void Heapify(int pole[], int dlzka, int index)
{
    int pravy, lavy, max;

    while(2 * index + 1 < dlzka)
    {
        lavy = 2 * index + 1;
        pravy = 2 * index + 2;

        // určenie potomka s maximálnou hodnotou
        if(pravy < dlzka && pole[pravy] > pole[lavy])
        {
            max = pravy;
        }
        else
        {
            max = lavy;
        }

        // porovnanie maximálneho potomka s rodičom
        if(pole[max] > pole[index])
        {

            Vymen(&pole[max], &pole[index]);
            index = max;
        }
        else
        {
            return;
        }
    }
}

void HeapSort(int pole[], int dlzka)
{
    // vytvor  maximálnu hromadu (procedúra BuildMaxHeap)
    for (int i = dlzka / 2 - 1 ; i >= 0; --i)
    {
        Heapify(pole, dlzka, i);
    }

    // zmaž všetky prvky z hromady
    for (int j = dlzka - 1; j > 0; --j)
    {
        Vymen(&pole[0], &pole[j]);
        Heapify(pole, j, 0);
    }
}

#include <stdio.h>

void Vymen(int *a, int *b);
void Heapify(int pole[], int dlzka, int index);
void HeapSort(int pole[], int dlzka);

int main()
{
    int pole[]= {10, 5, 2, 9, 8, 7, 1, 3, 4, 0, -1};
    int dlzka = sizeof(pole) / sizeof(pole[0]);

    HeapSort(pole, dlzka);

    for (int i = 0; i < dlzka; ++i)
    {
        printf("%d ", pole[i]);
    }
}


void Vymen(int *a, int *b)
{
    int tmp = *a;
    *a = *b;
    *b = tmp;
}

void Heapify(int pole[], int dlzka, int index)
{

    int lavy = 2 * index + 1;
    int pravy = 2 * index + 2;
    int max = index;

    // určenie potomka s maximálnou hodnotou
    if(lavy < dlzka && pole[lavy] >= pole[max])
    {
        max = lavy;
    }

    if(pravy < dlzka && pole[pravy] > pole[max])
    {
        max = pravy;
    }

    // porovnanie maximálneho potomka s rodičom
    if(pole[max] > pole[index])
    {
        Vymen(&pole[max], &pole[index]);
        Heapify(pole, dlzka, max);
    }
}

void HeapSort(int pole[], int dlzka)
{
    // vytvor  maximálnu hromadu (procedúra BuildMaxHeap)
    for (int i = dlzka / 2 - 1 ; i >= 0; --i)
    {
        Heapify(pole, dlzka, i);
    }

    // zmaž všetky prvky z hromady
    for (int j = dlzka - 1; j > 0; --j)
    {
        Vymen(&pole[0], &pole[j]);
        Heapify(pole, j, 0);
    }
}

#include <iostream>

using std::cout;
using std::endl;

void Vymen(int &a, int &b);
void Heapify(int pole[], int dlzka, int index);
void HeapSort(int pole[], int dlzka);

int main()
{
    int pole[]= {10, 5, 2, 9, 8, 7, 1, 3, 4, 0, -1};
    int dlzka = sizeof(pole) / sizeof(pole[0]);

    HeapSort(pole, dlzka);

    cout<<"Výsledné utriedené pole:"<<endl;

    for(auto i: pole)
    {
        cout<<i<<" ";
    }
}


void Vymen(int &a, int &b)
{
    int tmp = a;
    a = b;
    b = tmp;
}

void Heapify(int pole[], int dlzka, int index)
{
    int pravy, lavy, max;

    while(2 * index + 1 < dlzka)
    {
        lavy = 2 * index + 1;
        pravy = 2 * index + 2;

        // určenie potomka s maximálnou hodnotou
        if(pravy < dlzka && pole[pravy] > pole[lavy])
        {
            max = pravy;
        }
        else
        {
            max = lavy;
        }

        // porovnanie maximálneho potomka s rodičom
        if(pole[max] > pole[index])
        {

            Vymen(pole[max], pole[index]);
            index = max;
        }
        else
        {
            return;
        }
    }
}

void HeapSort(int pole[], int dlzka)
{
    // vytvor  maximálnu hromadu (procedúra BuildMaxHeap)
    for (int i = dlzka / 2 - 1 ; i >= 0; --i)
    {
        Heapify(pole, dlzka, i);
    }

    // zmaž všetky prvky z hromady
    for (int j = dlzka - 1; j > 0; --j)
    {
        Vymen(pole[0], pole[j]);
        Heapify(pole, j, 0);
    }
}

#include <iostream>

using std::cout;
using std::endl;

void Vymen(int &a, int &b);
void Heapify(int pole[], int dlzka, int index);
void HeapSort(int pole[], int dlzka);

int main()
{
    int pole[]= {10, 5, 2, 9, 8, 7, 1, 3, 4, 0, -1};
    int dlzka = sizeof(pole) / sizeof(pole[0]);

    HeapSort(pole, dlzka);

    cout<<"Výsledné utriedené pole:"<<endl;

    for(auto i: pole)
    {
        cout<<i<<" ";
    }

}


void Vymen(int &a, int &b)
{
    int tmp = a;
    a = b;
    b = tmp;
}

void Heapify(int pole[], int dlzka, int index)
{

    int lavy = 2 * index + 1;
    int pravy = 2 * index + 2;
    int max = index;

    // určenie potomka s maximálnou hodnotou
    if(lavy < dlzka && pole[lavy] > pole[max])
    {
        max = lavy;
    }

    if(pravy < dlzka && pole[pravy] > pole[max])
    {
        max = pravy;
    }

    // porovnanie maximálneho potomka s rodičom
    if(pole[max] > pole[index])
    {
        Vymen(pole[max], pole[index]);
        Heapify(pole, dlzka, max);
    }
}

void HeapSort(int pole[], int dlzka)
{
    // vytvor  maximálnu hromadu (procedúra BuildMaxHeap)
    for (int i = dlzka / 2 - 1 ; i >= 0; --i)
    {
        Heapify(pole, dlzka, i);
    }

    // zmaž všetky prvky z hromady
    for (int j = dlzka - 1; j > 0; --j)
    {
        Vymen(pole[0], pole[j]);
        Heapify(pole, j, 0);
    }
}

class HeapSortIT {
    void swap(int[] pole, int a, int b) {
        int tmp = pole[a];
        pole[a] = pole[b];
        pole[b] = tmp;
    }

    void heapify(int[] pole, int n) {
        for (int i = 1; i < n; i++) {

            /* Ak je potomok väčší ako rodič */
            if (pole[i] > pole[(i - 1) / 2]) {
                int j = i;

                /* Vymieňaj elementy (rodič, potomok), dokým je rodič menší ako potomok */
                while (pole[j] > pole[(j - 1) / 2]) {
                    swap(pole, j, (j - 1) / 2);
                    j = (j - 1) / 2;
                }
            }
        }
    }

    void sort(int[] pole) {
        int n = pole.length;

        heapify(pole, n);

        for (int i = n - 1; i > 0; i--) {
            int j = 0, index;

            /* Vymeň prvý a posledný prvok */
            swap(pole, 0, i);

            do {
                index = 2 * j + 1;

                /* Ak je ľavý potomok menši ako pravý, presuň 'index' na pravého potomka */
                if (index < i - 1 && pole[index] < pole[index + 1])
                    index++;

                /* Ak je rodič menší ako potomok, tak ho vymeň s potomkom, ktorý má väčšiu hodnotu */
                if (index < i && pole[j] < pole[index])
                    swap(pole, j, index);

                j = index;
            } while (index < i);
        }
    }
}

public class Main {

    static void printArray(int[] pole) {
        int n = pole.length;

        for (int i : pole)
            System.out.print(i + " ");

        System.out.println();
    }

    public static void main(String[] args) {
	    int[] pole = {12, 11, 13, 5, 6, 7};
	    int n = pole.length;

        System.out.println("Pole pred zoradenim: ");
        printArray(pole);

	    HeapSortIT hs = new HeapSortIT();
	    hs.sort(pole);

        System.out.println("Pole po zoradeni: ");
        printArray(pole);
    }
}

class HeapSortRE {
    void swap(int[] pole, int a, int b) {
        int tmp = pole[a];
        pole[a] = pole[b];
        pole[b] = tmp;
    }
    
    void heapify(int[] pole, int n, int i) {
        int max = i; // rodič
        int l = 2 * i + 1; // ľavý potomok
        int p = 2 * i + 2; // pravý potomok

        /* Ak je ľavý potomok väčší ako rodič */
        if (l < n && pole[l] > pole[max])
            max = l;

        /* Ak je pravý potomok väčší ako rodič */
        if (p < n && pole[p] > pole[max])
            max = p;

        /* Ak sa rodič v priebehu funkcie zmenil */
        if (max != i) {
            swap(pole, i, max);

            heapify(pole, n, max);
        }
    }

    public void sort(int[] pole) {
       int n = pole.length;

       /* Vytvorenie hromadu */
        for (int i = n / 2 - 1; i >= 0 ; i--)
            heapify(pole, n, i);

        /* Extrahovanie jednotlivých elemetov z hromady */
        for (int i = n - 1; i > 0; i--) {
            /* Presuň aktuálneho rodiča na koniec */
            swap(pole, 0, i);

            /* Zavolanie heapify na zredukovanú hromadu */
            heapify(pole, i, 0);
        }
    }
}

public class Main {

    static void printArray(int[] pole) {
        int n = pole.length;

        for (int i : pole)
            System.out.print(i + " ");

        System.out.println();
    }

    public static void main(String[] args) {
	    int[] pole = {12, 11, 13, 5, 6, 7};
	    int n = pole.length;

        System.out.println("Pole pred zoradenim: ");
        printArray(pole);

	    HeapSortRE hs = new HeapSortRE();
	    hs.sort(pole);

        System.out.println("Pole po zoradeni: ");
        printArray(pole);
    }
}

def heapify(pole, n):
    for i in range(n):

        # Ak je potomok väčší ako rodič
        if pole[i] > pole[int((i - 1) / 2)]:
            j = i

            # Vymieňaj elementy (rodič, potomok), dokým je rodič menší ako potomok
            while pole[j] > pole[int((j - 1) / 2)]:
                pole[j], pole[int((j - 1) / 2)] = pole[int((j - 1) / 2)], pole[j]       # swap
                j = int((j - 1) / 2)


def sort(pole, n):
    heapify(pole, n)

    for i in range(n - 1, 0, -1):

        # Vymeň prvý a posledný prvok
        pole[0], pole[i] = pole[i], pole[0]     # swap

        j, index = 0, 0

        while True:
            index = 2 * j + 1

            # Ak je ľavý potomok menši ako pravý, presuň 'index' na pravého potomka
            if index < (i - 1) and pole[index] < pole[index + 1]:
                index += 1

            # Ak je rodič menší ako potomok, tak ho vymeň s potomkom, ktorý má väčšiu hodnotu
            if index < i and pole[j] < pole[index]:
                pole[j], pole[index] = pole[index], pole[j]     # swap

            j = index

            if index >= i:
                break


def printArray(pole, n):
    for i in range(n):
        print(pole[i], end=" ")


if __name__ == '__main__':
    pole = [12, 11, 13, 5, 6, 7]
    n = len(pole)

    print("Zadane pole:")
    printArray(pole, n)

    sort(pole, n)

    print("\nZoradene pole:")
    printArray(pole, n)

def heapify(pole, n, i):
    max = i     # rodic
    l = 2 * i + 1       # lavy potomok
    p = 2 * i + 2       # pravy potomok

    # Ak je ľavý potomok väčší ako rodič
    if l < n and pole[max] < pole[l]:
        max = l

    # Ak je pravý potomok väčší ako rodič
    if p < n and pole[max] < pole[p]:
        max = p

    # Ak sa rodič v priebehu funkcie zmenil
    if max != i:
        pole[i], pole[max] = pole[max], pole[i]     # swap

        heapify(pole, n, max)


def sort(pole):
    n = len(pole)

    # Vytvorenie hromady
    for i in range(n // 2 - 1, -1, -1):
        heapify(pole, n, i)

    # Extrahovanie jednotlivých elementov z hromady
    for i in range(n - 1, 0, -1):
        pole[i], pole[0] = pole[0], pole[i]     # swap
        heapify(pole, i, 0)


def printArray(pole):
    n = len(pole)

    for i in range(n):
        print(pole[i], end=" ")


if __name__ == '__main__':
    pole = [12, 11, 13, 5, 6, 7]

    print("Zadane pole:")
    printArray(pole)

    sort(pole)

    print("\nZoradene pole:")
    printArray(pole)

Selection Sort

Vizualizácia algoritmu SelectionSort

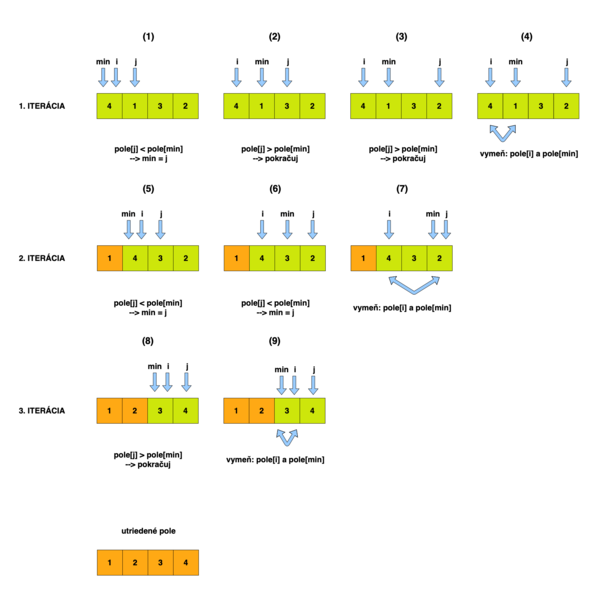
Prehľad

Selection Sort je triediaci algoritmus, ktorý si rozdelí pole na dve časti: zotriedenú a nezotriedenú. Následne opakovane vyberá minimum v nezotriedenej časti (ak triedime vzostupne), ktoré umiestni na koniec utrienej časti.

Vlastnosti algoritmu

• vhodný pre dátové štruktúry: pole
• časová náročnosť: vždy kvadratická [math] O(n^2) [/math], čo znamená, že algoritmus je určený na triedenie veľmi malých polí (rádovo 10, 20 prvkov), vďaka minimálnej réžii a jednoduchej implementácii, avšak pre väčšie polia sa stáva veľmi neefektívny
• priestorová náročnosť: vždy konštantná [math]O(1)[/math]
• druh triedenia: triedenie výberom (komparačný algoritmus)
• stabilita triedenia: nestabilný
• miesto triedenia: vnútorné triedenie

Základné časti algoritmu

1. Vonkajší cyklus: nastavenie hornej hranice utriedenej časti.
2. Vnútorný cyklus: hľadanie minima ....

Pseudokód

Nech má funkcia Selection Sort nasledovný prototyp: SelectionSort(pole[], dlzka)

1. Nech: min = pole[0]

2. Nech i = 1

3. Je i < dlzka ? Ak áno, pokračuj krokom 3.1., inak skonči.

3.1. Nech: j = i

3.2. Je j < dlzka ? Ak áno, pokračuj krokom 3.2.1. , inak skoč na krok 3.3.

3.2.1. Je pole[j] < min ?

Ak áno:

3.2.1.1. min = pole[j]

3.2.1.2. Skoč na krok 3.2.

Ak nie:

3.2.1.1. Skoč na krok 3.2.

3.3. Vymeň: pole[i] a pole[min]

3.4. Skoč na krok 3.2.

Odkazy

Heap Sort:

https://en.wikipedia.org/wiki/Heapsort

https://www.tutorialspoint.com/design_and_analysis_of_algorithms/design_and_analysis_of_algorithms_heapify_method.htm

https://www.geeksforgeeks.org/heap-sort/

https://www.geeksforgeeks.org/iterative-heap-sort/

https://www.youtube.com/watch?v=H5kAcmGOn4Q