Rádioaktívny rozpad: Rozdiel medzi revíziami
d |
|||
| (16 medziľahlých úprav od 2 ďalších používateľov nie je zobrazených) | |||
| Riadok 1: | Riadok 1: | ||
| + | {{sablona_python_priklady|Fyzika}} | ||
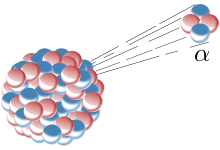
'''Rádioaktívny rozpad''' alebo jadrový rozpad je proces, pri ktorom nestabilné atómy strácajú svoju energiu vyžarovaním radiácie (žiarenia) vo forme častíc alebo elektromagnetických vĺn. Prvky, ktoré podliehajú radioaktívnemu rozpadu prirodzene (ich všetky izotopy podliehajú rádioaktívnemu rozpadu), sa nazývajú rádioaktívne prvky. | '''Rádioaktívny rozpad''' alebo jadrový rozpad je proces, pri ktorom nestabilné atómy strácajú svoju energiu vyžarovaním radiácie (žiarenia) vo forme častíc alebo elektromagnetických vĺn. Prvky, ktoré podliehajú radioaktívnemu rozpadu prirodzene (ich všetky izotopy podliehajú rádioaktívnemu rozpadu), sa nazývajú rádioaktívne prvky. | ||
| + | |||
| + | [[Súbor:2000px-Alpha Decay.svg.png]] | ||
==Prirodzená a umelá rádioaktivita== | ==Prirodzená a umelá rádioaktivita== | ||
| − | Rádioaktivita sa bežne rozdeľuje na | + | Rádioaktivita sa bežne rozdeľuje na |
| + | * prirodzenú | ||
| + | * umelú | ||
| + | Prirodzená rádioaktivita je dôsledkom samovoľného rozpadu atómového jadra. Umelú rádioaktivitu získajú prvky transmutáciou, vplyvom reťazovej reakcie alebo pôsobením urýchlených častíc. | ||
Príklad: | Príklad: | ||
| Riadok 28: | Riadok 34: | ||
kde <math>m_0</math> je počiatočná hmotnosť rádioaktívnej vzorky a <math>m</math> je jej hmotnosť v čase <math>t</math>. | kde <math>m_0</math> je počiatočná hmotnosť rádioaktívnej vzorky a <math>m</math> je jej hmotnosť v čase <math>t</math>. | ||
| − | === | + | === Polčas rozpadu === |
| − | Doba, za | + | Doba, za ktorú dôjde k rozpadu polovice z pôvodného počtu atómov rádionuklidu, sa označuje ako '''polčas rozpadu''' <math>T</math>. Počet častíc po uplynutí tejto doby je <math>N=\frac{N_0}{2}</math>, čím dostaneme pre polčas rozpadu vzťah |
:<math>T = \frac{\ln{2}}{\lambda}\approx 0,693\cdot\lambda^{-1}</math> | :<math>T = \frac{\ln{2}}{\lambda}\approx 0,693\cdot\lambda^{-1}</math> | ||
| − | === | + | === Stredná doba života === |
| − | + | Ďalšou veličinou charakterizujúcou rádioaktívny rozpad je '''stredná doba života''' <math>\tau</math>, čo je čas, za ktorý klesne pôvodný počet atómových jadier <math>N_0</math> na hodnotu <math>N=\frac{N_0}{\mathrm{e}}</math>. | |
| + | <br> | ||
| + | <br> | ||
| + | Pre strednú dobu života platí | ||
:<math>\tau = \frac{1}{\lambda} = \frac{T}{\ln{2}}</math> | :<math>\tau = \frac{1}{\lambda} = \frac{T}{\ln{2}}</math> | ||
| − | === Aktivita ( | + | === Aktivita (rádioaktivita) === |
| − | + | Rýchlosť rádioaktívnej premeny charakterizuje '''aktivita (rádioaktivita)''' <math>A</math>, ktorá sa definuje vzťahom | |
:<math>A = \left|\frac{\mathrm{d}n}{\mathrm{d}t}\right|</math> | :<math>A = \left|\frac{\mathrm{d}n}{\mathrm{d}t}\right|</math> | ||
| − | + | Dosadením z predchádzajúceho vzťahov dostaneme | |
:<math>A = \lambda n = \lambda n_0\mathrm{e}^{-\lambda t} = A_0\mathrm{e}^{-\lambda t}</math>, | :<math>A = \lambda n = \lambda n_0\mathrm{e}^{-\lambda t} = A_0\mathrm{e}^{-\lambda t}</math>, | ||
| − | kde <math>A_0</math> označuje aktivitu v | + | kde <math>A_0</math> označuje aktivitu v počiatočnom čase a <math>A</math> je aktivita v čase <math>t</math>. Aktivita, teda rýchlost rozpadu, klesá s časem. |
| + | |||
| + | Jednotkou aktivity je '''becquerel (Bq)''', popr. curie (Ci). | ||
| + | |||
| + | == Druhy rádioaktívneho žiarenia == | ||
| + | Žiarenie, ktoré pri rádioaktívnom rozpade vzniká, má štyri druhy, ktoré označujeme ako α, β, γ a neutrónové žiarenie. | ||
| + | |||
| + | * '''Žiarenie α''' je prúd jadier hélia (α-častíc) a nesie kladný elektrický náboj, má najkratší dosah (zastaví ho napr. i list papiera). | ||
| + | |||
| + | * '''Žiarenie β''' je prúd záporne nabitých elektrónov. Niekedy sa rozlišuje žiarenie β<sup>-</sup> (elektróny) a β<sup>+</sup> (kladne nabité pozitróny), zachytí ho 1 cm plexiskla alebo 1 mm olova. | ||
| + | |||
| + | * '''Žiarenie γ''' je elektromagnetické žiarenie vysokej frekvencie, resp. prúd veľmi energetických fotónov. Nemá elektrický náboj, a preto nereaguje na elektrické pole. Jeho prenikavosť je veľmi vysoká, pre zatienenie sa používajú veľmi tlsté štíty z kovov veľkej hustoty (napr. olovo) alebo zliatin kovov veľkej hustoty. Platí, že čím vyššia hustota a hrúbka štítu, tým viac je žiarenie zatienené. | ||
| + | |||
| + | * '''Neutrónové žiarenie''' je prúd neutrónov. Nemá elektrický náboj. Pohltí ho hrubá vrstva vody alebo betónu. | ||
| + | [[Súbor:150px-Radioactive_decay_modes.svg.png]] | ||
| + | |||
| + | == Rozpadové rady == | ||
| + | Kvantová mechanika umožňuje pre každý izotop spočítať pravdepodobnosť, že jadro sa v danom časovom intervale rozpadne. Pre väčšie množstvo látky je možné určiť polčas rozpadu, ktorým charakterizujeme rýchlosť premeny. Udáva, za ako dlho sa rozpadne práve polovica jadier vo vzorke. U tažkých prvkov sú produkty rozpadu takisto nestabilné a rozpadajú se ďalej. Tento proces popisuje rozpadová rada. | ||
| + | |||
| + | == Časový priebeh rádioaktívneho rozpadu == | ||
| + | Graf znázorňuje časové závislosti počtu rozpadnutých jadier N pre 3 rôzne hodnoty <math>{\lambda}</math> počas prvých piatich sekúnd rozpadu.<br> | ||
| + | Program využíva '''Zákon rádioaktívneho rozpadu'''.<br> | ||
| + | [[Súbor:Zakon rad.premeny.png]]<br> | ||
| + | '''Zdrojový kód pre graf (Python 2.7.1)''' | ||
| + | |||
| + | <source lang="python"> | ||
| + | from pylab import * | ||
| + | |||
| + | x=linspace(0,5,100000) | ||
| + | x1=linspace(0,5,100000) | ||
| + | x2=linspace(0,5,100000) | ||
| + | m=10^6 | ||
| + | y=m*exp(-0.1*x) | ||
| + | y1=m*exp(-1*x1) | ||
| + | y2=m*exp(-10*x2) | ||
| + | plot(x,y,x1,y1,x2,y2) | ||
| + | title("Casova zavislost radioaktivnej premeny") | ||
| + | legend(('lambda=0.1','lambda=1','lambda=10')) | ||
| + | xlabel("Cas [t]") | ||
| + | ylabel("Pocet castic [N]") | ||
| + | grid(1) | ||
| + | show() | ||
| + | </source> | ||
| − | + | == Zaujímavosti == | |
| + | * Rádioaktívny rozpad poskytol prvý dôkaz toho, že zákony riadiace subatómový svet majú štatistický charakter. | ||
| + | * Neexistuje vôbec žiadny spôsob, ako predpovedať, či určité jadro zo vzorky bude jedným z malého počtu jadier, ktoré se rozpadnú v nasledujúcej sekunde. U všetkých jadier je pravdepodobnosť rovnaká. | ||
Aktuálna revízia z 10:34, 18. marec 2013
Rádioaktívny rozpad alebo jadrový rozpad je proces, pri ktorom nestabilné atómy strácajú svoju energiu vyžarovaním radiácie (žiarenia) vo forme častíc alebo elektromagnetických vĺn. Prvky, ktoré podliehajú radioaktívnemu rozpadu prirodzene (ich všetky izotopy podliehajú rádioaktívnemu rozpadu), sa nazývajú rádioaktívne prvky.
Obsah
Prirodzená a umelá rádioaktivita
Rádioaktivita sa bežne rozdeľuje na
- prirodzenú
- umelú
Prirodzená rádioaktivita je dôsledkom samovoľného rozpadu atómového jadra. Umelú rádioaktivitu získajú prvky transmutáciou, vplyvom reťazovej reakcie alebo pôsobením urýchlených častíc.
Príklad: Polónium [math]{}_{84}^{210}Po[/math] je prirodzene rádioaktívny, pričom pri svojom rozpade vyžaruje α častice, ktoré premieňajú hliník na izotop fosforu.
- [math]{}_{13}^{27}Al + {}_2^4\alpha \,\to\, {}_{15}^{30}P + n[/math],
kde [math]n[/math] označuje neutrón. Izotop fosforu [math]{}_{15}^{30}P[/math] je však nestabilný s polčasom rozpadu. [math]T\approx 135,5\,\mbox{s}[/math]. Prostredníctvom kladného beta rozpadu prechádzajú na stabilný kremík, tzn.
- [math]{}_{15}^{30}P\,\to\, {}_{14}^{30}Si + e^{+} + \nu[/math],
kde [math]e^{+}[/math] je vyžiarený pozitron a [math]\nu[/math] predstavuje neutríno.
Zákon radioaktivního rozpadu
Vlastnosti rádioaktívneho rozpadu je možné skúmať pomocou štatistických metód.
Za predpokladu, že za časový interval [math]\mathrm{d}t[/math] dôjde k rozpadu [math]\mathrm{d}N[/math] atómov rádioaktívnej látky. Počet rozpadnutých atómov [math]\mathrm{d}N[/math] je úmerný počtu častíc v danom časovom okamihu, ktorý označíme [math]N[/math]. Túto úmeru vyjadrujeme vzťahom
- [math]-\mathrm{d}N = \lambda N \mathrm{d}t[/math],
kde [math]\lambda[/math] je tzv. rozpadová konštanta, ktorá charakterizuje predpokladanú rýchlosť rozpadu rádionuklidu. Znamienko - súvisí s tým, že s rastúcim časom dochádza k poklesu okamžitého počtu častíc.
Integráciou predchádzajúceho vzťahu môžeme počet častíc v čase [math]t[/math] vyjadriť ako
- [math]N = N_0\mathrm{e}^{-\lambda t}[/math],
kde [math]N_0[/math] predstavuje počet častíc v čase [math]t=0[/math]. Tento vzťah sa označuje ako zákon rádioaktívneho rozpadu.
Pre praktické využitie je vhodnejšie využiť úmeru mezdi počtom častíc a ich celkovou hmotnosťou, tzn. hmotnosťou rádioaktívnej vzorky [math]m[/math]. Predchádzajúci vzťah potom môžeme prepísať v tvare
- [math]m = m_0\mathrm{e}^{-\lambda t}[/math],
kde [math]m_0[/math] je počiatočná hmotnosť rádioaktívnej vzorky a [math]m[/math] je jej hmotnosť v čase [math]t[/math].
Polčas rozpadu
Doba, za ktorú dôjde k rozpadu polovice z pôvodného počtu atómov rádionuklidu, sa označuje ako polčas rozpadu [math]T[/math]. Počet častíc po uplynutí tejto doby je [math]N=\frac{N_0}{2}[/math], čím dostaneme pre polčas rozpadu vzťah
- [math]T = \frac{\ln{2}}{\lambda}\approx 0,693\cdot\lambda^{-1}[/math]
Stredná doba života
Ďalšou veličinou charakterizujúcou rádioaktívny rozpad je stredná doba života [math]\tau[/math], čo je čas, za ktorý klesne pôvodný počet atómových jadier [math]N_0[/math] na hodnotu [math]N=\frac{N_0}{\mathrm{e}}[/math].
Pre strednú dobu života platí
- [math]\tau = \frac{1}{\lambda} = \frac{T}{\ln{2}}[/math]
Aktivita (rádioaktivita)
Rýchlosť rádioaktívnej premeny charakterizuje aktivita (rádioaktivita) [math]A[/math], ktorá sa definuje vzťahom
- [math]A = \left|\frac{\mathrm{d}n}{\mathrm{d}t}\right|[/math]
Dosadením z predchádzajúceho vzťahov dostaneme
- [math]A = \lambda n = \lambda n_0\mathrm{e}^{-\lambda t} = A_0\mathrm{e}^{-\lambda t}[/math],
kde [math]A_0[/math] označuje aktivitu v počiatočnom čase a [math]A[/math] je aktivita v čase [math]t[/math]. Aktivita, teda rýchlost rozpadu, klesá s časem.
Jednotkou aktivity je becquerel (Bq), popr. curie (Ci).
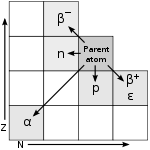
Druhy rádioaktívneho žiarenia
Žiarenie, ktoré pri rádioaktívnom rozpade vzniká, má štyri druhy, ktoré označujeme ako α, β, γ a neutrónové žiarenie.
- Žiarenie α je prúd jadier hélia (α-častíc) a nesie kladný elektrický náboj, má najkratší dosah (zastaví ho napr. i list papiera).
- Žiarenie β je prúd záporne nabitých elektrónov. Niekedy sa rozlišuje žiarenie β- (elektróny) a β+ (kladne nabité pozitróny), zachytí ho 1 cm plexiskla alebo 1 mm olova.
- Žiarenie γ je elektromagnetické žiarenie vysokej frekvencie, resp. prúd veľmi energetických fotónov. Nemá elektrický náboj, a preto nereaguje na elektrické pole. Jeho prenikavosť je veľmi vysoká, pre zatienenie sa používajú veľmi tlsté štíty z kovov veľkej hustoty (napr. olovo) alebo zliatin kovov veľkej hustoty. Platí, že čím vyššia hustota a hrúbka štítu, tým viac je žiarenie zatienené.
- Neutrónové žiarenie je prúd neutrónov. Nemá elektrický náboj. Pohltí ho hrubá vrstva vody alebo betónu.
Rozpadové rady
Kvantová mechanika umožňuje pre každý izotop spočítať pravdepodobnosť, že jadro sa v danom časovom intervale rozpadne. Pre väčšie množstvo látky je možné určiť polčas rozpadu, ktorým charakterizujeme rýchlosť premeny. Udáva, za ako dlho sa rozpadne práve polovica jadier vo vzorke. U tažkých prvkov sú produkty rozpadu takisto nestabilné a rozpadajú se ďalej. Tento proces popisuje rozpadová rada.
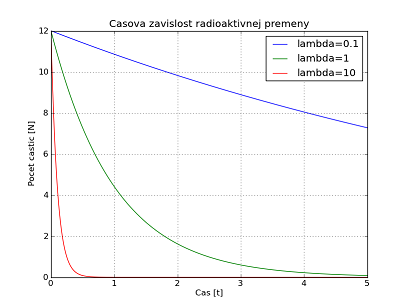
Časový priebeh rádioaktívneho rozpadu
Graf znázorňuje časové závislosti počtu rozpadnutých jadier N pre 3 rôzne hodnoty [math]{\lambda}[/math] počas prvých piatich sekúnd rozpadu.
Program využíva Zákon rádioaktívneho rozpadu.
Zdrojový kód pre graf (Python 2.7.1)
from pylab import *
x=linspace(0,5,100000)
x1=linspace(0,5,100000)
x2=linspace(0,5,100000)
m=10^6
y=m*exp(-0.1*x)
y1=m*exp(-1*x1)
y2=m*exp(-10*x2)
plot(x,y,x1,y1,x2,y2)
title("Casova zavislost radioaktivnej premeny")
legend(('lambda=0.1','lambda=1','lambda=10'))
xlabel("Cas [t]")
ylabel("Pocet castic [N]")
grid(1)
show()
Zaujímavosti
- Rádioaktívny rozpad poskytol prvý dôkaz toho, že zákony riadiace subatómový svet majú štatistický charakter.
- Neexistuje vôbec žiadny spôsob, ako predpovedať, či určité jadro zo vzorky bude jedným z malého počtu jadier, ktoré se rozpadnú v nasledujúcej sekunde. U všetkých jadier je pravdepodobnosť rovnaká.