Java - algoritmy interpolácie: Rozdiel medzi revíziami
(Vytvorená stránka „{{navigacne menu - java}} Interpolácia je matematický algoritmus, kde máme k dispozícii ''n'' bodov v rovine XY a úlohou je nájsť taký polynóm, ktorý prechádza c…“) |
|||
| Riadok 64: | Riadok 64: | ||
<math>\ell_j(x) = \prod_{i=0,\, i\neq j}^{n} \frac{x-x_i}{x_j-x_i} = \frac{(x-x_0)}{(x_j-x_0)} \cdots \frac{(x-x_{j-1})}{(x_j-x_{j-1})} \frac{(x-x_{j+1})}{(x_j-x_{j+1})} \cdots \frac{(x-x_{n})}{(x_j-x_{n})}</math> | <math>\ell_j(x) = \prod_{i=0,\, i\neq j}^{n} \frac{x-x_i}{x_j-x_i} = \frac{(x-x_0)}{(x_j-x_0)} \cdots \frac{(x-x_{j-1})}{(x_j-x_{j-1})} \frac{(x-x_{j+1})}{(x_j-x_{j+1})} \cdots \frac{(x-x_{n})}{(x_j-x_{n})}</math> | ||
| − | Kde L(x) je výsledný | + | Kde L(x) je výsledný interpolačný polynóm a <math>\ell_j(x)</math> sú Lagrangeove interpolačné polynómy (stupňa j). |
==Riešenie v jazyku Java== | ==Riešenie v jazyku Java== | ||
| − | Triedu Extrapolacia.java doplníme o nasledujúcu metódu | + | Pre implementáciu Lagrangeovho tvaru interpolačného polynómu využijeme triedu Extrapolator. Vstupné body sú rovnako ako pri aproximácii uložené v zozname bodov ''body''. |
| + | |||
| + | Triedu Extrapolacia.java doplníme o nasledujúcu metódu ''interpolacia''. Premenné v cykloch majú rovnaký názov ako indexy vo vzorcoch. V kóde je nutné najskôr vypočítať Lagrangeov interpolačný polynóm stupňa j (j sa mení sa od 0 do n) a následne sa sčítajú výrazy <math>y_jl_j(x)</math>. | ||
<source lang="java"> | <source lang="java"> | ||
| Riadok 87: | Riadok 89: | ||
} | } | ||
</source> | </source> | ||
| + | |||
| + | Pre vykreslenie priebehu interpolačného polynómu použijeme kód podobný ako pri aproximácii. Do aplikácie pridáme tlačidlo 'Interpoluj', priradíme mu názov ''tlcInterpoluj'' a pridáme mu udalosť ''ActionPerformed'': | ||
| + | |||
| + | <source lang="java"> | ||
| + | private void tlcInterpolujActionPerformed(java.awt.event.ActionEvent evt) { | ||
| + | int sirka, vyska; //sirka a vyska panelu na kreslenie | ||
| + | sirka = panel.getWidth(); | ||
| + | vyska = panel.getHeight(); | ||
| + | t.setSize(sirka, vyska); | ||
| + | |||
| + | g = panel.getGraphics(); | ||
| + | g.setColor(Color.GRAY); // osy X, Y | ||
| + | g.drawLine(0, vyska / 2, sirka, vyska / 2); | ||
| + | g.drawLine(sirka / 2, 0, sirka / 2, vyska); | ||
| + | |||
| + | //vykreslovanie interpolacneho polynomu | ||
| + | g.setColor(Color.BLUE); | ||
| + | //realne hodnoty, s ktorymi pocitame | ||
| + | double x1, y1, x2, y2 = 0; | ||
| + | //hodnoty v pixeloch | ||
| + | int X1, Y1, X2, Y2; | ||
| + | x1 = -t.getStrana(); | ||
| + | y1 = e.interpolacia(x1); | ||
| + | for (x2 = -t.getStrana(); x2 < t.getStrana(); x2 += t.getKrok()) { | ||
| + | y2 = e.interpolacia(x2); | ||
| + | X1 = t.getX(x1); | ||
| + | X2 = t.getX(x2); | ||
| + | Y1 = t.getY(y1); | ||
| + | Y2 = t.getY(y2); | ||
| + | g.drawLine(X1, Y1, X2, Y2); | ||
| + | x1 = x2; | ||
| + | y1 = y2; | ||
| + | } | ||
| + | |||
| + | //vykreslenie vstupnych bodov | ||
| + | g.setColor(Color.BLACK); | ||
| + | for(int i=0;i<e.body.size();i++) | ||
| + | { | ||
| + | g.drawOval(t.getX(e.body.get(i).x)-3,t.getY(e.body.get(i).y)-3, 6, 6); | ||
| + | } | ||
| + | } | ||
| + | </source> | ||
| + | |||
| + | |||
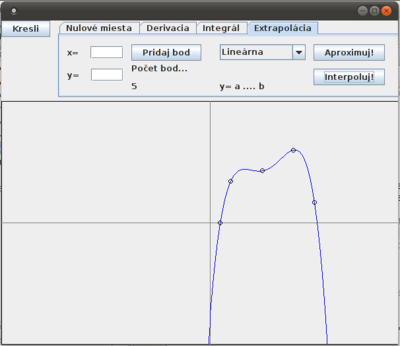
| + | '''Výledok''' | ||
| + | |||
| + | [[Súbor:lagrangeov interpolacny polynom Java aplikacia.png|center|thumb|400px|Implementácia interpolačného polynómu v Lagrangeovom tvare]] | ||
Aktuálna revízia z 09:06, 11. máj 2011
Základy informatiky - jazyk Java
Úvod do programovania v jazyku Java
Java - objektovo orientovaný prístup
Vzorové príklady:
Java - implementácia numerických algoritmov
- >Java - algoritmy hľadania nulových miest
>Java - algoritmy numerického derivovania
>Java - algoritmy numerického integrovania
>Java - algoritmy aproximácie
>Java - algoritmy interpolácie
Java - triedy geometrických tvarov
Pokročilé témy:
Interpolácia je matematický algoritmus, kde máme k dispozícii n bodov v rovine XY a úlohou je nájsť taký polynóm, ktorý prechádza cez všetky zadané body. Pri n bodoch dokážeme vypočítať polynóm stupňa n-1. Všeobecný tvar polynómu je:
[math]f(x)=a_nx^n+a_{n+1}x^{n-1}+...+a_1x+a_0[/math]
Interpolačný polynóm
Najpriamejším (aj keď nie najjednoduchším) spôsobom ako vypočítať interpolačný polynóm je jednoducho dosadiť známe body do predchádzajúcej rovnice. Vznikne nám tak sústava n rovníc o n neznámych. Majme nasledujúce body:
| x | 1 | 2 | 5 | 8 | 10 |
|---|---|---|---|---|---|
| y | 0 | 4 | 7 | 5 | 2 |
Pre tieto body dostávame sústavu rovníc:
[math] \begin{array}{lcr} 0=a_4 1^4 + a_3 1^3 + a_2 1^2 + a_1 1^1 + a_0 1^0 \\ 4=a_4 2^4 + a_3 2^3 + a_2 2^2 + a_1 2^1 + a_0 2^0 \\ 7=a_4 5^4 + a_3 5^3 + a_2 5^2 + a_1 5^1 + a_0 5^0 \\ 5=a_4 8^4 + a_3 8^3 + a_2 8^2 + a_1 8^1 + a_0 8^0 \\ 2=a_4 10^4 + a_3 10^3 + a_2 10^2 + a_1 10^1 + a_0 10^0 \\ \end{array} [/math]
Čo môžeme zapísať ako maticovú rovnicu:
[math] \begin{pmatrix} 1^4 & 1^3 & 1^2 & 1^1 & 1^0 \\ 2^4 & 2^3 & 2^2 & 2^1 & 2^0 \\ 5^4 & 5^3 & 5^2 & 5^1 & 5^0 \\ 8^4 & 8^3 & 8^2 & 8^1 & 8^0 \\ 10^4 & 10^3 & 10^2 & 10^1 & 10^0 \\ \end{pmatrix} \begin{pmatrix} a_0\\ a_1\\ a_2\\ a_3\\ a_4\\ \end{pmatrix}= \begin{pmatrix} 0\\ 4\\ 7\\ 5\\ 2\\ \end{pmatrix} [/math]
Túto maticovú rovnicu môžeme riešiť napríklad Gausovou eliminačnou metódou.
Lagrangeov tvar interpolačného polynómu
Pre dané body existuje iba jeden itnerpolačný polynóm. Rozdiel je len v spôsobe ako sa tento polynóm vypočíta. Lagrangeov interpolačný polynóm využíva špeciálny tvar polynómov, ktoré sa nazývajú Lagrangeove polynómy. Pre Langrangeov tvar intepolačného polynómu platia nasledujúce vzťahy:
[math]L(x) = \sum_{j=0}^{n} y_j \ell_j(x) [/math]
[math]\ell_j(x) = \prod_{i=0,\, i\neq j}^{n} \frac{x-x_i}{x_j-x_i} = \frac{(x-x_0)}{(x_j-x_0)} \cdots \frac{(x-x_{j-1})}{(x_j-x_{j-1})} \frac{(x-x_{j+1})}{(x_j-x_{j+1})} \cdots \frac{(x-x_{n})}{(x_j-x_{n})}[/math]
Kde L(x) je výsledný interpolačný polynóm a [math]\ell_j(x)[/math] sú Lagrangeove interpolačné polynómy (stupňa j).
Riešenie v jazyku Java
Pre implementáciu Lagrangeovho tvaru interpolačného polynómu využijeme triedu Extrapolator. Vstupné body sú rovnako ako pri aproximácii uložené v zozname bodov body.
Triedu Extrapolacia.java doplníme o nasledujúcu metódu interpolacia. Premenné v cykloch majú rovnaký názov ako indexy vo vzorcoch. V kóde je nutné najskôr vypočítať Lagrangeov interpolačný polynóm stupňa j (j sa mení sa od 0 do n) a následne sa sčítajú výrazy [math]y_jl_j(x)[/math].
public double interpolacia(double x) {
double lag, lag_pol = 0;
int j, i;
for (j = 0; j < this.body.size() ; j++) {
lag = 1.0;
for (i = 0; i < this.body.size() ; i++) {
if (i == j) {
continue;
}
lag *= (x - this.body.get(i).x) / (this.body.get(j).x - this.body.get(i).x);
}
lag_pol += this.body.get(j).y * lag;
}
return lag_pol;
}
Pre vykreslenie priebehu interpolačného polynómu použijeme kód podobný ako pri aproximácii. Do aplikácie pridáme tlačidlo 'Interpoluj', priradíme mu názov tlcInterpoluj a pridáme mu udalosť ActionPerformed:
private void tlcInterpolujActionPerformed(java.awt.event.ActionEvent evt) {
int sirka, vyska; //sirka a vyska panelu na kreslenie
sirka = panel.getWidth();
vyska = panel.getHeight();
t.setSize(sirka, vyska);
g = panel.getGraphics();
g.setColor(Color.GRAY); // osy X, Y
g.drawLine(0, vyska / 2, sirka, vyska / 2);
g.drawLine(sirka / 2, 0, sirka / 2, vyska);
//vykreslovanie interpolacneho polynomu
g.setColor(Color.BLUE);
//realne hodnoty, s ktorymi pocitame
double x1, y1, x2, y2 = 0;
//hodnoty v pixeloch
int X1, Y1, X2, Y2;
x1 = -t.getStrana();
y1 = e.interpolacia(x1);
for (x2 = -t.getStrana(); x2 < t.getStrana(); x2 += t.getKrok()) {
y2 = e.interpolacia(x2);
X1 = t.getX(x1);
X2 = t.getX(x2);
Y1 = t.getY(y1);
Y2 = t.getY(y2);
g.drawLine(X1, Y1, X2, Y2);
x1 = x2;
y1 = y2;
}
//vykreslenie vstupnych bodov
g.setColor(Color.BLACK);
for(int i=0;i<e.body.size();i++)
{
g.drawOval(t.getX(e.body.get(i).x)-3,t.getY(e.body.get(i).y)-3, 6, 6);
}
}
Výledok