Pružné kĺby: Rozdiel medzi revíziami
| (4 medziľahlé úpravy od 2 ďalších používateľov nie sú zobrazené) | |||
| Riadok 2: | Riadok 2: | ||
[[Kategória:Bakalárske práce]] | [[Kategória:Bakalárske práce]] | ||
[[Kategória:Mechatronika]] | [[Kategória:Mechatronika]] | ||
| − | {{Praca_uvod|4|Použitie mikrouchopovačov MEMS | + | {{Praca_uvod|4|Použitie mikrouchopovačov MEMS|Čo je to MEMS alebo MST?|Základné problémy pri návrhu mikrouchopovača|Pružné Mechanizmy|Pružné kĺby|Materiál pre mikrouchopovače|Návrh mikrouchopovača|Riešenie pružných mechanizmov pomocou metódy konečných prvkov}} |
= = | = = | ||
| Riadok 45: | Riadok 45: | ||
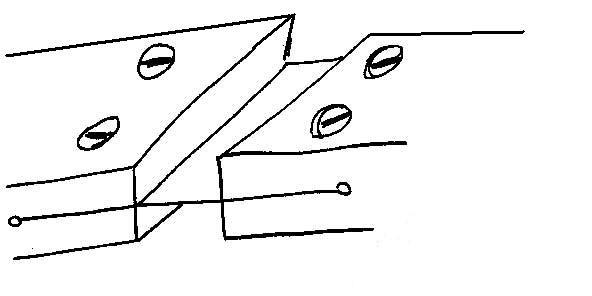
[[Image:dvojosý pružný kĺb.jpg|center|framed|Obr 4.4 jdvojosý pružný kĺb ]] | [[Image:dvojosý pružný kĺb.jpg|center|framed|Obr 4.4 jdvojosý pružný kĺb ]] | ||
| + | |||
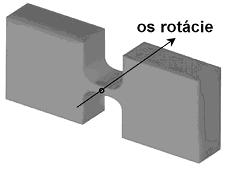
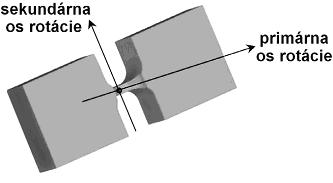
| + | V trojrozmerných systémoch sa dá využiť aj viacosý kĺb (Obr. 4.5), ktorý umožňuje ohyb v rôznych smeroch [3]. | ||
| + | |||
| + | [[Image:viacosý pružný kĺb.jpg|center|framed|Obr 4.5 viacosý pružný kĺb ]] | ||
| + | |||
| + | ==Tvary pružných kĺbov== | ||
| + | Asi najviac využívané pružné kĺby v praxi čo sa týka dvojrozmerných systémov sú kĺby s kruhovým zárezom (Obr. 4.6a), trámovy kĺb (Obr. 4.6b), poprípade krížový kĺb (Obr. 4.6c). Samozrejme by sa dalo hovoriť aj o rôznych ďalších možných riešeniach ale kvôli jednoduchosti a ľahkému vyhotoveniu sa väčšinou používajú vyššie uvedené. Hlavnou ich výhodou je však schopnosť redukovať koncentráciu napätia vďaka ich zaobleným častiam v rohoch. | ||
| + | |||
| + | [[Image:tvary pružných kĺbov.jpg|center|framed|Obr 4.6 a) pružný kĺb s kruhovým zárezom, b) pružný trámový kĺb, c) pružný krížový kĺb ]] | ||
| + | |||
| + | |||
| + | ==Návrh pružných kĺbov== | ||
| + | |||
| + | Keďže pružné kĺby zabezpečujú pohyb pružných mechanizmov, je kladený obrovský dôraz na ich presnosť a hlavne tvar. Aj ta najmenšia zmena tvaru kĺbu môže ovplyvniť výsledný efekt pri pohybe mechanizmu. | ||
| + | Pri návrhu treba preto zvážiť hľadiská: | ||
| + | • vykonanie požadovanej rotácie, ohybu, | ||
| + | • zabezpečenie žiadanej presnosti rotácie, | ||
| + | • vyhovieť napätiam, vzniknutým pri ohybe, | ||
| + | • vyhovieť požiadavkám na spotrebu alebo akumuláciu energie. | ||
| + | |||
| + | Konečné požiadavky na mechanizmus: | ||
| + | • pevnosť, tuhosť, | ||
| + | • spotreba energie, | ||
| + | • presnosť výstupného pohybu.[3], [1] | ||
| + | |||
| + | Pri navrhovaní pružných kĺbov treba správne zvolenie vlastností. A to tuhosť v smere rotácie ψ, tuhosť v smere x-ovej a z-ovej osi, ohybové napätie v smere ψ a tiež napätia spôsobené normálovou silou F<sub>n</sub> [4]. | ||
| + | |||
| + | ===Kĺb s kruhovým zárezom=== | ||
| + | Keďže pri návrhu nášho mikrouchopovača budeme využívať len kĺb s kruhovým zárezom, budeme sa detailnejšie venovať len tomuto typu kĺbu. | ||
| + | |||
| + | [[Súbor:Popis rozmerov pružného kĺbu s kruhovým zárezom.png|center|frame|Obr. 4.7: Popis rozmerov pružného kĺbu s kruhovým zárezom]] | ||
| + | |||
| + | Vlastnosti pružného kĺbu s kruhovým zárezom, vyjadrené pomocou metódy konečných prvkov, sú reprezentované vzťahmi podľa literatúry [4]. | ||
| + | |||
| + | Tuhosť v smere osi x: | ||
| + | |||
| + | {{Vzorec|<math>\frac{{{C}_{x}}}{E.t}=0,0010+0,4256\sqrt{\frac{h}{D}}+0,824{{\left( \sqrt{\frac{h}{D}} \right)}^{2}}</math> | ||
| + | |4.1}} | ||
| + | |||
| + | |||
| + | Tuhosť v smere z: | ||
| + | |||
| + | {{Vzorec|<math>\frac{{{C}_{z}}}{E.t}=0,0040+0,0727\sqrt{\frac{h}{D}}+0,3417{{\left( \sqrt{\frac{h}{D}} \right)}^{2}}</math>|4.2}} | ||
| + | |||
| + | |||
| + | Tuhosť v smere ψ: | ||
| + | |||
| + | {{Vzorec|<math>\frac{12.{{k}_{\psi }}}{E.t.{{h}^{2}}}=-0,0089+1,3556\sqrt{\frac{h}{D}}-0,5227{{\left( \sqrt{\frac{h}{D}} \right)}^{2}}</math>|4.3}} | ||
| + | |||
| + | |||
| + | Ohybové napätie v smere ψ: | ||
| + | |||
| + | {{Vzorec| | ||
| + | <math>\frac{{{\sigma }_{\psi }}}{E.\psi }=-0,0028+0,6397\sqrt{\frac{h}{D}}-0,0856{{\left( \sqrt{\frac{h}{D}} \right)}^{2}}</math>|4.4}} | ||
| + | |||
| + | |||
| + | Napätie spôsobené normálovou silou F<sub>n</sub>: | ||
| + | {{Vzorec| | ||
| + | <math>\frac{{{\sigma }_{x}}.h.t}{Fn}=0,9951+0,0542\sqrt{\frac{h}{D}}+0,5171{{\left( \sqrt{\frac{h}{D}} \right)}^{2}}</math>|4.5}} | ||
| + | |||
| + | [[Image:Graf pre kĺb s kruhovým zárezom.png|center|framed|Graf 4.1: Graf pre kĺb s kruhovým zárezom]] | ||
Aktuálna revízia z 18:59, 11. december 2010
Obsah
Pružný kĺb je prvok v rámci konštrukcie, ktorý vďaka svojej pružnosti umožňuje pohyb medzi dvoma susediacimi nehybnými časťami.
Pružný kĺb môžeme zabezpečiť pomocou pružného elementu ako je napríklad tenký oceľový pásik uchytený medzi pevné nepohybujúce sa časti.
Pružný kĺb môžeme dosiahnuť aj opracovaním materiálu tak, aby v mieste ohybu vznikol vrub, teda vytvorí sa ohybové tenké spojítko. V tomto prípade predchádzame rozdeleniu materiálu.
Výhody pružných kĺbov
Berme do úvahy len monolitické pružné kĺby. Keďže sú vyrobené z jedného kusa materiálu majú oproti mechanickým značné výhody:
- Žiadne straty spôsobené trením
- Nie je potrebné mazanie
- Nie sú citlivé na znečistenie
- Uloženie je bez vôle
- Žiadna hysterézia
- Kompaktnosť
- Jednoduché zhotovenie
- Prakticky žiadna potrebná údržba
Nevýhody pružných kĺbov
Nevýhody sa týkajú najmä obmedzení:
- Kĺby sú schopné poskytnúť pomerne nízku úroveň rotácii.
- Rotácie nie je čistá, pretože vzniká axiálne strihanie prípadne aj torzia zaťaženia, okrem ohýbania.
- Ohýbanie kĺbu je zvyčajne citlivé voči zmenám teploty.
Jeho rozmery sa menia v dôsledku tepelnej rozťažnosti čo vedie k zmenám oproti pôvodným hodnotám. Mechanizmus s kĺbmi bude fungovať, kým sa niečo nepokazí. Zvyčajne to býva samotný kĺb v dôsledku únavy alebo preťaženia materiálu.
Osové otáčanie pružných kĺbov
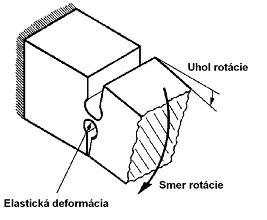
Pružné kĺby sa rozdeľujú aj podľa pohybu. V dvojrozmerných systémoch sa využívajú kĺby, ktoré umožňujú pohyb iba okolo jednej osi. Je to os okolo ktorej sa otáčajú neohybné pevné časti. Sú to tzv. jednoosé pružné kĺby (Obr. 4.3).
V trojrozmerných systémoch sú zas zapracované dvojosé kĺby (Obr. 4.4). Tieto kĺby umožňujú ohyb okolo dvoch osí, ktoré sú na seba kolmé.
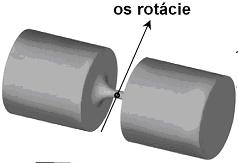
V trojrozmerných systémoch sa dá využiť aj viacosý kĺb (Obr. 4.5), ktorý umožňuje ohyb v rôznych smeroch [3].
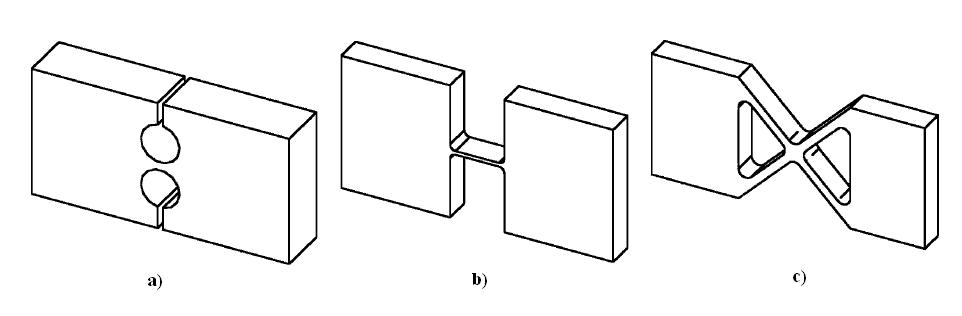
Tvary pružných kĺbov
Asi najviac využívané pružné kĺby v praxi čo sa týka dvojrozmerných systémov sú kĺby s kruhovým zárezom (Obr. 4.6a), trámovy kĺb (Obr. 4.6b), poprípade krížový kĺb (Obr. 4.6c). Samozrejme by sa dalo hovoriť aj o rôznych ďalších možných riešeniach ale kvôli jednoduchosti a ľahkému vyhotoveniu sa väčšinou používajú vyššie uvedené. Hlavnou ich výhodou je však schopnosť redukovať koncentráciu napätia vďaka ich zaobleným častiam v rohoch.
Návrh pružných kĺbov
Keďže pružné kĺby zabezpečujú pohyb pružných mechanizmov, je kladený obrovský dôraz na ich presnosť a hlavne tvar. Aj ta najmenšia zmena tvaru kĺbu môže ovplyvniť výsledný efekt pri pohybe mechanizmu. Pri návrhu treba preto zvážiť hľadiská: • vykonanie požadovanej rotácie, ohybu, • zabezpečenie žiadanej presnosti rotácie, • vyhovieť napätiam, vzniknutým pri ohybe, • vyhovieť požiadavkám na spotrebu alebo akumuláciu energie.
Konečné požiadavky na mechanizmus: • pevnosť, tuhosť, • spotreba energie, • presnosť výstupného pohybu.[3], [1]
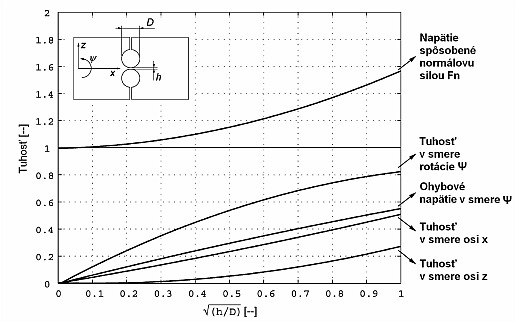
Pri navrhovaní pružných kĺbov treba správne zvolenie vlastností. A to tuhosť v smere rotácie ψ, tuhosť v smere x-ovej a z-ovej osi, ohybové napätie v smere ψ a tiež napätia spôsobené normálovou silou Fn [4].
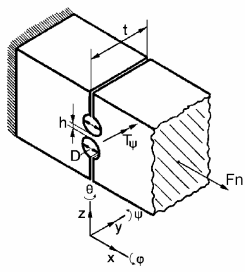
Kĺb s kruhovým zárezom
Keďže pri návrhu nášho mikrouchopovača budeme využívať len kĺb s kruhovým zárezom, budeme sa detailnejšie venovať len tomuto typu kĺbu.
Vlastnosti pružného kĺbu s kruhovým zárezom, vyjadrené pomocou metódy konečných prvkov, sú reprezentované vzťahmi podľa literatúry [4].
Tuhosť v smere osi x:
|
[math]\frac{{{C}_{x}}}{E.t}=0,0010+0,4256\sqrt{\frac{h}{D}}+0,824{{\left( \sqrt{\frac{h}{D}} \right)}^{2}}[/math] |
(4.1) |
Tuhosť v smere z:
|
[math]\frac{{{C}_{z}}}{E.t}=0,0040+0,0727\sqrt{\frac{h}{D}}+0,3417{{\left( \sqrt{\frac{h}{D}} \right)}^{2}}[/math] |
(4.2) |
Tuhosť v smere ψ:
|
[math]\frac{12.{{k}_{\psi }}}{E.t.{{h}^{2}}}=-0,0089+1,3556\sqrt{\frac{h}{D}}-0,5227{{\left( \sqrt{\frac{h}{D}} \right)}^{2}}[/math] |
(4.3) |
Ohybové napätie v smere ψ:
|
[math]\frac{{{\sigma }_{\psi }}}{E.\psi }=-0,0028+0,6397\sqrt{\frac{h}{D}}-0,0856{{\left( \sqrt{\frac{h}{D}} \right)}^{2}}[/math] |
(4.4) |
Napätie spôsobené normálovou silou Fn:
|
[math]\frac{{{\sigma }_{x}}.h.t}{Fn}=0,9951+0,0542\sqrt{\frac{h}{D}}+0,5171{{\left( \sqrt{\frac{h}{D}} \right)}^{2}}[/math] |
(4.5) |