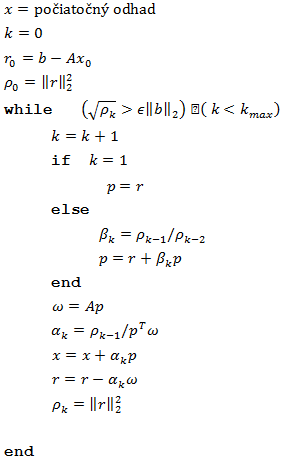Moderné metódy riešenia veľkých sústav rovníc

Obsah práce

1.	Sústavy lineárnych rovníc a matice
2.	Klasické metódy riešenia sústav lineárnych rovníc
3.	Priame metódy pre riešenie veľkých sústav rovníc
4.	Moderné metódy riešenia veľkých sústav rovníc
5.	Softvérové balíky pre riešenie veľkých lineárnych systémov

V tejto časti sú opísané niektoré z moderných iteračných metód, ktoré sú vhodné pre riešenie veľmi veľkých a riedkych matíc. Sú tu opísané gradientné metódy a taktiež multigridové metódy. Tieto metódy využívajú mnohé zo simulačných softvérov, kde je potrebné riešiť veľké riedke sústavy lineárnych rovníc.

Metóda konjugovaných gradientov (CG)

Väčšina iteračných metód je závislá na parametroch, avšak niekedy je veľmi náročné zvoliť správne parametre. Toto nie je potrebné pri metóde konjugovaných gradientov (Conjugate Gradient Method). Táto metóda sa používa pre riešenie pre veľkých riedkych systémov, pretože sa v nej často využíva len násobenie matice sústavy vektorom. Metóda konjugovaných gradientov je vhodná pre symetrické a kladne definitné systémy[3]. </nowiki>

Majme systém rovníc Ax=b, kde A je štvorcová symetrická kladne definitná matica.

Využíva sa tu fakt, že riešenie takejto sústavy je jediným minimom nasledovnej formy:

[math]\phi \left( x \right)=\frac{1}{2}{{x}^{T}}Ax-{{x}^{T}}b[/math]

(4.1)

[3][9]

Minimum funkcie [math]\phi \left( x \right)[/math] je [math]-{{b}^{T}}{{A}^{-1}}b/2[/math], čo sme dostali dosadením za x , [math]x={{A}^{-1}}b[/math].

Potom teda minimalizácia funkcie [math]\phi \left( x \right)[/math] a riešenie rovnice [math]Ax=b[/math], sú ekvivalentné problémy ak je matica A symetrická kladne definitná.

Jedným z najjednoduchších spôsobov pre minimalizáciu je tzv. metóda najväčšieho spádu. V nejakom bode [math]x_c[/math] funkcia ϕ klesá najviac v smere záporného gradientu:[math]-\nabla \phi \left( {{x}_{c}} \right)=b-A{{x}_{c}}[/math].

Potom [math]{{r}_{c}}=b-A{{x}_{c}}[/math]. Hovoríme že, rc je reziduálny vektor v bode xc. Ak je reziduálny vektor nenulový , potom existuje kladné α , také že [math]\phi \left( {{x}_{c}}+\alpha {{r}_{c}} \right)\lt \phi \left( {{x}_{c}} \right)[/math]. Pre minimalizáciu dosadíme za α:

[math]\alpha =\frac{r_{c}^{T}{{r}_{c}}}{r_{c}^{T}A{{r}_{c}}}[/math]

[math]\phi \left( {{x}_{c}}+\alpha {{r}_{c}} \right)=\phi \left( {{x}_{c}} \right)-\alpha r_{c}^{T}{{r}_{c}}+\frac{1}{2}{{\alpha }^{2}}r_{c}^{T}A{{r}_{c}}[/math]

Budeme uvažovať o minimalizácii pozdĺž smerov {p1,p2,....} . V tejto metóde sa volia vektory pk tak, že vzniknú A-ortogonalizáciou vektora rezíduí . A-ortogonalizácia umožňuje z postupnosti lineárne nezávislých vektorov u1 , ... , un zostrojiť inú postupnosť lineárne nezávislých vektorov v1 , ... , vn tak , že bude platiť nasledovný vzťah [math]v_{i}^{T}A{{v}_{j}}=0\,pre\,i\ne j[/math]

Možno dokázať, že minimum funkcie [math]\phi \left( {{x}_{k-1}}+\alpha {{p}_{k}} \right)[/math] dostaneme pre

[math]\alpha ={{\alpha }_{k}}=p_{k}^{T}{{r}_{k-1}}/p_{k}^{T}A{{p}_{k}}[/math].

Dostávame [math]{{x}_{k}}={{x}_{k-1}}+{{\alpha }_{k}}{{p}_{k}}[/math], kde [math]p_k[/math] je spádový smer a [math]{{\alpha }_{k}}[/math] je optimálny krok[3].

Ak [math]{{r}_{k-1}}\ne 0[/math], potom existuje [math]p_k[/math] také, že [math]p_{k}^{T}{{r}_{k-1}}\ne 0[/math]. Keď je [math]k=1[/math] potom [math]{{p}_{1}}={{r}_{0}}[/math]. Pre k > 1 potom platí : [math]{{p}_{k}}={{r}_{k-1}}+{{\beta }_{k}}{{p}_{k-1}}[/math].

Keď [math]p_{k-1}^{T}A{{p}_{k}}=0\lt /math, potom dostávame vzťah : \lt math\gt {{\beta }_{k}}=-\frac{p_{k-1}^{T}A{{r}_{k-1}}}{p_{k-1}^{T}A{{p}_{k-1}}}[/math]

Reziduálny vektor [math]r_k[/math] môžeme vyjadriť ako [math]{{r}_{k}}={{r}_{k-1}}-{{\alpha }_{k}}A{{p}_{k}}[/math].

Potom použitím nasledovných substitúcií [math]\begin{align} & r_{k-1}^{T}{{r}_{k-1}}=-{{\alpha }_{k-1}}r_{k-1}^{T}A{{p}_{k-1}} \\ & r_{k-2}^{T}{{r}_{k-2}}={{\alpha }_{k-1}}p_{k-1}^{T}A{{p}_{k-1}} \\ \end{align}[/math]

vo vzťahu pre [math]{{\beta }_{k}}[/math] dostávame výsledný algoritmus.

Algoritmus CG

k=0
r_0=b-Ax_0
while   r_k≠0
	k=k+1
	if    k=1
		p_1=r_0	
	else
		β_k=r_(k-1)^T*r_(k-1)/r_(k-2)^T*r_(k-2)
		p_k=r_(k-1)+β_k*p_(k-1)
	end
	α_k=r_(k-1)^T*r_(k-1)/p_k^T*Ap_k
              x_k=x_(k-1)+α_k*p_k
              r_k=r_(k-1)+α_k*Ap_k
end 
x=x_k

V praxi sa však používa obmenená verzia tohto algoritmu, pretože zaokrúhľovacie chyby vedú k strate ortogonálnosti nad rezidúami a preto by nebolo zaručené ukončenie algoritmu. Preto je ukončenie algoritmu založené na maxime iterácií kmax a norme rezidua a danej presnosti ϵ. Toto vedie k nasledovnému algoritmu .

Upravený algoritmus CG:

Metóda konjugovaných gradientov konverguje k riešeniu sústavy rovníc o n neznámych najneskôr za n krokov. Tento algoritmus vyžaduje jedno násobenie matica-vektor a 10n flops za jednu iteráciu [3] .

Ilustračný príklad riešenia prostredníctvom metódy CG

Pre ilustráciu riešenia prostredníctvom metódy konjugovaných gradientov riešme jednoduchý príklad. Majme sústavu lineárnych rovníc Ax=b , kde A je symetrická matica o rozmeroch 2×2.

[math]\text{A}=\left[ \begin{matrix} 2 & 1 \\ 1 & 3 \\ \end{matrix} \right],\ x=\left[ \begin{matrix} {{x}_{1}} \\ {{x}_{2}} \\ \end{matrix} \right],\ b=\left[ \begin{matrix} 2 \\ 3 \\ \end{matrix} \right][/math]

Najprv zvolíme počiatočný odhad riešenia x0 .

[math]x=\left[ \begin{matrix} 1 \\ 1 \\ \end{matrix} \right][/math]

Riešenie Určíme reziduálny vektor [math]r_0[/math] ku [math]x_0[/math] prostredníctvom vzťahu [math]r_0=b-Ax_0[/math]. V našom prípade :

[math]{{r}_{0}}=\left[ \begin{matrix} 2 \\ 3 \\ \end{matrix} \right]-~\left[ \begin{matrix} 2 & 1 \\ 1 & 3 \\ \end{matrix} \right]\left[ \begin{matrix} 1 \\ 1 \\ \end{matrix} \right]=~\left[ \begin{matrix} 2 \\ 3 \\ \end{matrix} \right]-~\left[ \begin{matrix} 3 \\ 4 \\ \end{matrix} \right]=\left[ \begin{matrix} -1 \\ -1 \\ \end{matrix} \right][/math]

Toto je prvá iterácia , preto zvolíme za smer [math]p_0[/math] reziduálny vektor [math]r_0[/math]. Ďalej určíme skalár [math]α_0[/math] nasledovne

[math]{{\alpha }_{0}}=\frac{r_{0}^{T}{{r}_{0}}}{p_{0}^{T}A{{p}_{0}}}=\frac{\begin{matrix} \left[ \begin{matrix} -1 & -1 \\ \end{matrix} \right] & \left[ \begin{matrix} -1 \\ -1 \\ \end{matrix} \right] \\ \end{matrix}}{\begin{matrix} \left[ \begin{matrix} -1 & -1 \\ \end{matrix} \right] & \left[ \begin{matrix} 2 & 1 \\ 1 & 3 \\ \end{matrix} \right] & \left[ \begin{matrix} -1 \\ -1 \\ \end{matrix} \right] \\ \end{matrix}}=\frac{2}{7}[/math]

Vypočítame [math]x_1[/math] použitím nasledovného vzorca :

[math]{{x}_{1}}={{x}_{0}}+{{\alpha }_{0}}{{p}_{0}}=\left[ \begin{matrix} 1 \\ 1 \\ \end{matrix} \right]+\frac{2}{7}\left[ \begin{matrix} -1 \\ -1 \\ \end{matrix} \right]=\left[ \begin{matrix} 0.7143 \\ 0.7143 \\ \end{matrix} \right][/math]

Týmto sme ukončili prvú iteráciu a určili sme presnejšie približné riešenie systému . Teraz určíme ďalší reziduálny vektor [math]r_1[/math]:

[math]{{r}_{1}}={{r}_{0}}-{{\alpha }_{0}}A{{p}_{0}}=\left[ \begin{matrix} -1 \\ -1 \\ \end{matrix} \right]-\frac{2}{7}~\left[ \begin{matrix} 2 & 1 \\ 1 & 3 \\ \end{matrix} \right]~\left[ \begin{matrix} -1 \\ -1 \\ \end{matrix} \right]=\left[ \begin{matrix} -0.1429 \\ -0.1428 \\ \end{matrix} \right][/math]

Ďalším krokom výpočtu je určenie skalára [math]β_0[/math] ktorý sa použije na určenie ďalšieho smeru [math]p_1[/math]

[math]{{\beta }_{0}}=\frac{r_{1}^{T}{{r}_{1}}}{r_{0}^{T}{{r}_{0}}}=\frac{\left[ \begin{matrix} -0.1429 & -0.1428 \\ \end{matrix} \right]\left[ \begin{matrix} -0.1429 \\ -0.1428 \\ \end{matrix} \right]}{\begin{matrix} \left[ \begin{matrix} -1 & -1 \\ \end{matrix} \right] & \left[ \begin{matrix} -1 \\ -1 \\ \end{matrix} \right] \\ \end{matrix}}=0.0204[/math]

Teraz skalár [math]β_0[/math] použijeme pre určenie ďalšieho smeru [math]p_1[/math]

[math]{{p}_{1}}={{r}_{1}}+{{\beta }_{0}}{{p}_{0}}=\left[ \begin{matrix} -0.1429 \\ -0.1428 \\ \end{matrix} \right]+0,0204~\left[ \begin{matrix} -1 \\ -1 \\ \end{matrix} \right]=\left[ \begin{matrix} -0,1633 \\ 0,1224 \\ \end{matrix} \right][/math]

Určíme α_1 podobne ako predtým [math]α_0[/math] , ale teraz použijeme nový smer [math]p_1[/math]

[math]{{\alpha }_{1}}=\frac{r_{1}^{T}{{r}_{1}}}{p_{1}^{T}A{{p}_{1}}}=\frac{\begin{matrix} \left[ \begin{matrix} -0.1429 & -0.1428 \\ \end{matrix} \right] & \left[ \begin{matrix} -0.1429 \\ -0.1428 \\ \end{matrix} \right] \\ \end{matrix}}{\begin{matrix} \left[ \begin{matrix} -0,1633 & 0,1224 \\ \end{matrix} \right] & \left[ \begin{matrix} 2 & 1 \\ 1 & 3 \\ \end{matrix} \right] & \left[ \begin{matrix} -0,1633 \\ 0,1224 \\ \end{matrix} \right] \\ \end{matrix}}=0.6999[/math]

Nakoniec určíme [math]x_2[/math] podobným spôsobom ako predtým [math]x_1[/math] [10].

[math]{{x}_{2}}={{x}_{1}}+{{\alpha }_{1}}{{p}_{1}}=\left[ \begin{matrix} 0.7143 \\ 0.7143 \\ \end{matrix} \right]+0.6999\left[ \begin{matrix} -0,1633 \\ 0,1224 \\ \end{matrix} \right]=\left[ \begin{matrix} 0.600006 \\ 0.799967 \\ \end{matrix} \right][/math]

Dostávame riešenie sústavy [math]x=\left[ \begin{matrix} 0.600006 \\ 0.799967 \\ \end{matrix} \right][/math]

Overenie výsledku pomocou priamej metódy

Pre určenie presného riešenia sústavy použijeme Cramerovo pravidlo. Pre danú sústavu Ax=b , kde [math]\text{A}=\left[ \begin{matrix} 2 & 1 \\ 1 & 3 \\ \end{matrix} \right],\ x=\left[ \begin{matrix} {{x}_{1}} \\ {{x}_{2}} \\ \end{matrix} \right],\ b=\left[ \begin{matrix} 2 \\ 3 \\ \end{matrix} \right][/math]

Najprv zvolíme počiatočný odhad riešenia x0 .

[math]x=\left[ \begin{matrix} 1 \\ 1 \\ \end{matrix} \right][/math] určíme najskôr determinant sústavy [math]D=\left| \begin{matrix} 2 & 1 \\ 1 & 3 \\ \end{matrix} \right|=2*3-1*1=5[/math]

Potom nahradíme prvý stĺpec matice A vektorom pravých strán b a určíme determinant:

[math]{{D}_{1}}=\left| \begin{matrix} 2 & 1 \\ 3 & 3 \\ \end{matrix} \right|=2*3-1*3=3[/math]

Podobne nahradíme druhý stĺpec matice A a dostávame :

[math]{{D}_{2}}=\left| \begin{matrix} 2 & 2 \\ 1 & 3 \\ \end{matrix} \right|=2*3-2*1=4[/math]

Teraz určíme riešenie sústavy:

[math]\begin{align} & {{x}_{1}}=\frac{{{D}_{1}}}{D}=\frac{3}{5}=0.6 \\ & {{x}_{2}}=\frac{{{D}_{2}}}{D}=\frac{4}{5}=0.8 \\ \end{align}[/math]