Algoritmy hľadania nulových miest

Algoritmy a programovanie

---

Dátový typ

Štruktúry

Rekurzia

Algoritmy vyhľadávania

Algoritmy triedenia

Lineárny zoznam

Binárny strom

Numerické algoritmy

>Algoritmy hľadania nulových miest
>Algoritmy numerického derivovania
>Algoritmy numerického integrovania
>Algoritmy interpolácie
>Algoritmy aproximácie
>Algoritmy numerického riešenia diferenciálnych rovníc

Grafové algoritmy

Algoritmy hľadania nulových miest (A root-finding algorithms), sú také algoritmy ktoré hľadajú takú hodnotu x, pre ktorú platí f(x)=0, pre danú funkcie f.

Hľadanie nulových miest rovnice [math]f(x) − g(x) = 0[/math] je totožné s riešením rovnice [math]f(x) = g(x)[/math], kde x je neznáma. Inak povedané, ľubovoľnú rovnicu môžeme vyjadriť v kanonickom tvare [math]f(x) = 0[/math], takže riešenie takejto rovnice je vlastne hľadaním nulového bodu funkcie. Prvý odhad riešenia rovnice je počiatočný návrh. Zvolená metóda (algoritmus) vypočítava postupnosť hodnôt, ktoré berú v ohľad predchádzajúcu vypočítanú hodnotu a riešenú funkciu f.

Vo všetkých nasledujúcich algoritmoch hľadáme také x, pre ktoré platí : [math]f(x)=0[/math]

Newtonova metóda nulových miest

Pre danú funkciu [math]f(x)[/math] a je algoritmus definovaný pomocou vzorca

[math]x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}. \,\![/math]

kde

[math]{f'(x_n)}. \,\![/math] je prvá derivácia funkcie [math]{f(x_n)}. \,\![/math]

Hodnota [math]x_0[/math] je prvý odhad riešenia. Výpošet skončíme vtedy, keď sa hodnota [math]{f(x_n)}. \,\![/math] blíži k nule.

Odvodenie Newtonovho vzorca

Vieme, že derivácia funkcie je limita podielu rozdielov 2 funkčných hodnôt a prislúchajúcich hodnôt na osi x, pričom vzdialenosť týchto hodnôt na osi x sa limitne blíži k nule.

[math]{f}'\left( x \right)=\underset{{{x}_{n}}-{{x}_{n+1}}\to 0}{\mathop{\lim }}\,\frac{f\left( {{x}_{n}} \right)-f\left( {{x}_{n+1}} \right)}{{{x}_{n}}-{{x}_{n+1}}}[/math]

Tento vzťah môžeme vyjadriť pomocou diferencií nasledovne:

[math]{f}'({{x}_{n}})=\frac{\Delta \text{y}}{\Delta \text{x}}=\frac{f({{x}_{n}})-f({{x}_{n+1}})}{{{x}_{n}}-{{x}_{n+1}}}[/math]

Ak uvažujeme, že [math]x_{n+1}[/math] ako presné riešenie, potom [math]f(x_{n+1})=0[/math] a rovnicu môžeme prepísať nasledovne

[math]{f}'({{x}_{n}})=\frac{\Delta \text{y}}{\Delta \text{x}}=\frac{f({{x}_{n}})-0}{{{x}_{n}}-{{x}_{n+1}}}[/math]

Z čoho môžme vyjadriť [math]x_{n+1}[/math] ako:

[math]x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}. \,\![/math]

čo sme chceli dokázať.

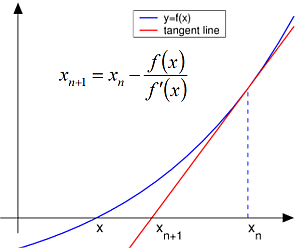
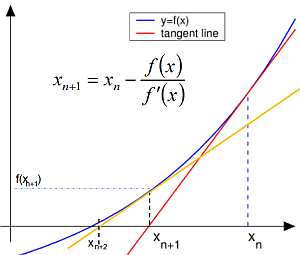
Geometrická interpretácia riešenia

Newtonova metóda sa nazýva aj metóda dotyčníc, podľa jej geometrického významu V geometrickej interpretácii Newtonovho vzorca je bod [math][x_{k+1},0][/math] prienikom dotyčnice zostrojenej v bode [math][x_k,f(x_k)][/math] ku krivke [math]y=f(x)[/math] a x-ovej osi. Preto Newtonovej metóde hovoríme aj metóda dotyčníc.

Prvá iterácia. [math]x_n[/math] je prvý odhad. Hodnota [math]x_{n+1}[/math] je priesečník dotyčnice funkcie f(x) v bode [math]x_n[/math] s osou x

Druhá iterácia. [math]x_{n+1}[/math] je prvý vypočítaná hodnota. Hodnota [math]x_{n+2}[/math] je priesečník dotyčnice funkcie f(x) v bode [math]x_{n+1}[/math] s osou x. Hodnota [math]x_{n+2}[/math] sa približuje presnému riešeniu.

Riešenie v jazyku C

Pre výpočet nulových bodov potrebujeme:

• Rovnicu v tvare f(x)=0
• Deriváciu podľa x : f´(x)

Daný Newtonov vzorec je rekurzívny, čo využijeme pri programovaní. Pri rekurzívnych funkciách treba definovať podmienku, kedy sa funkcia ukončí rekurzívne volanie. V tomto prípade je podmienka prostá: keď sa priblížime k riešeniu s dostatočnou presnosťou. Vyjadrené matematickým vzorcom: Funkcia ukončí rekurzívne volanie ak platí že [math]f(x_n)\lt \epsilon[/math], kde [math]\epsilon[/math] je požadovaná presnosť.

V príklade budeme hľadať riešenie rovnice:

[math]f(x)=cos(x)+x^3[/math]

prvá derivácia tejto funkcie je:

[math]f'(x)=-sin(x)+3x^2[/math]

Riešenie č. 1

double fx(double x) 
{	
   return (cos(x) + x*x*x); 
}
double dfx(double x)
{
   return (-sin(x) + 3*x*x); 
}
double NewtonRoot1(double x0=1.0,double epsilon=0.01)
{
   if( fx1(x0) < epsilon)
      return x0;
   else
      return NewtonRoot1( x0-fx1(x0)/dfx1 (x0) );
}
// použitie

int main()
{
   double x;
   x=NewtonRoot1();
   cout<<"Riesenie rovnice cos(x) + x*x*x=0 : x="<<x;
}

Riešenie č. 2

V tomto riešení využijeme smerník na funkciu ako parameter funkcie NewtonRoot. Táto zmena má nasledovné výhody

• Funkcia NewtonRoot má informáciu o tom, pre ktorú funkciu sa počíta nulový bod. Smerník na túto funkciu je parametrom funkcie NewtonRoot.
• Pomocou parametrov funkcie dokážem jednoducho zmeniť rovnicu pre ktorú hľadám nulový bod (bez zmeny tela funkcie NewtonRoot)

double fx1(double x) 
{	
   return (cos(x) + x*x*x); 
}
double dfx1(double x)
{
   return (-sin(x) + 3*x*x); 
}

double fx2(double x) 
{	
   return (cos(x*x) + x*x); 
}
double dfx2(double x)
{
   return (-sin(x)*2*x + 2*x); 
}

double NewtonRoot2(double (*f)(double), double (*f_der)(double),double x0=1.0,double epsilon=0.01)
{
   if( f(x0) < epsilon)
      return x0;
   else
      return NewtonRoot2(f , f_der , x0-f(x0)/f_der(x0) );
}
// použitie

int main()
{
   double x;
   x=NewtonRoot2(fx1,dfx1);
   cout<<"Riesenie rovnice cos(x) + x*x*x=0 : x="<<x;

   x=NewtonRoot2(fx2,dfx2);
   cout<<"Riesenie rovnice cos(x*x) + x*x=0 : x="<<x;
}

Riešenie č. 3

Obmedzujúcim faktorom je to, že musíme vypočítať prvú deriváciu riešenej funkcie. V prípade, ak dokážeme prvú deriváciu vypočítať pomocou nejakého algoritmu (Algoritmy numerického derivovania), využijeme to a vytvoríme funkciu, ktorá dokáže zderivovať ľubovoľnú spojitú matematickú funkciu.

double dfx(double (*f)(double ),double x)
{
   double h=0.0000000001;
   return (f(x+h)-f(x))/h;
}
double fx1(double x) 
{	
   return (cos(x) + x*x*x); 
}
double fx2(double x) 
{	
   return (cos(x*x) + x*x); 
}

double NewtonRoot3(double (*f)(double ),double x0=1.0,double epsilon=0.01)
{ 
   if( f(x0) < epsilon)
      return x0;
   else
      return NewtonRoot3(f, x0-f(x0)/dfx(f,x0) );
}
// použitie

int main()
{
   double x;
   x=NewtonRoot3(fx1);
   cout<<"Riesenie rovnice cos(x) + x*x*x=0 : x="<<x;

   x=NewtonRoot3(fx2);
   cout<<"Riesenie rovnice cos(x*x) + x*x=0 : x="<<x;
}

Pozor pri funkcii dfx, pretože výpočet prvej derivácie musí byť dostatočne presný, keďže chyba derivácie sa nám postupne šíri celým riešením. Toto riešenie je najmenej presné a závisí práve od presnosti derivácie.

Metóda polenia intervalov

Táto metóda je taktiež známa ako bisekčná metóda.

Polenie intervalov sa využíva pri hľadaná približného riešenia rovníc. Ak nájdeme také 2 čísla, pre ktoré platí [math]sgn(f(x1)) = - sgn(f(x2)) \,\![/math], kde sgn znamená znamienkovú funkciu signum. Ďalej určíme hodnotu [math]x_0 = \frac{x_1 + x_2}{2}[/math]. Podľa hodnoty f(x0) potom postupujeme nasledovne:

1. ak platí [math]f(x0) = 0[/math] našli sme nulový bod
2. ak platí: [math]f(x_0) \neq 0[/math]: zistíme, v ktorom z bodov x1 a x2 má funkcia f rovnaké znamienko ako v bode x0
   • Ak je to bod x1, potom uvažujme x1 = x0
   • Ak je to bod x2, potom uvažujme x2 = x0

Ak s[ body x1 a x2 blízko seba (teda x2 − x1 < ε, kde ε je požadovaná presnosť), potom sme našli približné riešenie. V opačnom prípade sa vrátime na začiatok a celý postup opakujeme, ale na intervale polovičnej dĺžky.

Pseudo kód

 opakuj pokiaľ platí ( abs(right - left) > 2*epsilon)
   
   //Vypočítaj stredný bod intervalu
   midpoint = (right + left) / 2
   
   //určovanie intervalu
   ak ((f(left) * f(midpoint)) < 0) tak
     //hľadanie riešenia bude v pravej časti
     right = midpoint
   inak ak ((f(right) * f(midpoint)) < 0)
     //hľadanie riešenia bude v pravej časti
     left = midpoint
   inak
    // ukonči cyklus, našli sme riešenie - midpoint
 koniec cyklu
 Vráť midpoint

Riešenie v jazyku C

double fx1(double x) 
{	
   return (cos(x) + x*x*x); 
}
double fx2(double x) 
{	
   return (x*x-3); 
}

double bis_met(double a, double b,double (*f)(double))
{
  // predpoklad správneho riesenia:
  // jedna z hodnot f(a),f(b) musi byt mensia ako 0, druha vascia
  double lo, hi,mid;     
  if (f(a) <= 0)
  { 
     lo = a;
     hi = b;
  }
  else
  {
    lo = b;
    hi = a;
  }

  mid = lo + (hi-lo)/2;
  while ((mid != lo) && (mid != hi)) 
  { 
     if (f(mid) <= 0)
        lo = mid;
     else
        hi = mid;
     mid = lo + (hi-lo)/2;
  }
 
  return mid;
}

// použitie
int main()
{
   double x;
   x=bis_met(0,2,fx1);
   cout<<"Riesenie rovnice cos(x) + x*x*x=0 : x="<<x;
   cout<<endl;

   x=bis_met(0,2,fx2);
   cout<<"Riesenie rovnice x*x - 3=0 : x="<<x;
   cout<<endl;

  getch();
}

n-tá odmocnina

Tento algoritmus je veľmi rýchly a hľadá riešenie rovnice

[math]x^n = A [/math]

alebo inak povedané, hľadáme n-tú odmocninu čísla A: [math]\sqrt[n]{A}[/math]

naša funkcia f(x) vyzerá nasledovne: [math]f(x)=\sqrt[n]{A}[/math]

Algoritmus

1. Nastav počiatočnú hodnotu [math]x_0[/math] (prvý odhad riešenia)
2. Nastav [math]x_{k+1} = \frac{1}{n} \left[{(n-1)x_k +\frac{A}{x_k^{n-1}}}\right][/math]
3. opakuj krok 2 pokiaľ nie je dosiahnutá požadovaná presnosť.

Požadovanú presnosť môžeme určiť tak, že ak rozdiel hodnôt x_{k+1} a x_{k} je menší ako požadované presnosť, výpočet skončí.

Špeciálnym prípadom tohto algoritmu je výpočet druhej odmocniny, kde sa nám vzorec zjednoduší na nasledujúcu verziu:

[math]x_{k+1} = \frac{1}{2}\left(x_k + \frac{A}{x_k}\right)[/math]

double nth_root(double A,int n,double x0=1.0,double epsilon=0.01)
{
   double x=1.0/n*( (n-1)*x0 + A/pow(x0,n-1) );
   if(fabs(x-x0)<epsilon)
     return x;
   return nth_root(A,n,x);
}

// použitie
int main()
{
   cout<<nth_root(125,5);
   getch();
}

Odkazy

• http://en.wikipedia.org/wiki/Newton%27s_method
• http://mathworld.wolfram.com/NewtonsMethod.html
• http://en.wikipedia.org/wiki/Bisection_method
• http://mathworld.wolfram.com/Bisection.html