Chaotické riešenie diferenciálnych rovníc - Rösslerov atraktor: Rozdiel medzi revíziami
Skočit na navigaci
Skočit na vyhledávání
| Riadok 7: | Riadok 7: | ||
: <math>\frac{dz}{dt} = b + z(x-c)</math> | : <math>\frac{dz}{dt} = b + z(x-c)</math> | ||
| − | Sústava rovníc vykazuje pri vhodnom výbere vstupných parametrov ''a, b, c'' chaotické<ref>http://en.wikipedia.org/wiki/Chaos_theory</ref><ref>http://cs.wikipedia.org/wiki/Teorie_chaosu</ref><ref>http://sk.wikipedia.org/wiki/Te%C3%B3ria_chaosu</ref> nedeterministické riešenie. Simulačný model vytvoríme priamym prepisom sústavy rovníc do grafickej podoby pomocou [[Knižnica_komponentov_gsim | komponentov ]] Xspice. | + | Sústava rovníc vykazuje pri vhodnom výbere vstupných parametrov ''a, b, c'' chaotické<ref>http://en.wikipedia.org/wiki/Chaos_theory</ref><ref>http://cs.wikipedia.org/wiki/Teorie_chaosu</ref><ref>http://sk.wikipedia.org/wiki/Te%C3%B3ria_chaosu</ref> nedeterministické riešenie. Simulačný model vytvoríme priamym prepisom integrálneho tvaru sústavy rovníc do grafickej podoby pomocou [[Knižnica_komponentov_gsim | komponentov ]] Xspice. |
<center> | <center> | ||
Verzia zo dňa a času 08:44, 1. apríl 2010
Rösslerova sústava[1][2] diferenciálnych rovníc má tvar
- [math]\frac{dx}{dt} = -y - z[/math]
- [math]\frac{dy}{dt} = x + ay[/math]
- [math]\frac{dz}{dt} = b + z(x-c)[/math]
Sústava rovníc vykazuje pri vhodnom výbere vstupných parametrov a, b, c chaotické[3][4][5] nedeterministické riešenie. Simulačný model vytvoríme priamym prepisom integrálneho tvaru sústavy rovníc do grafickej podoby pomocou komponentov Xspice.
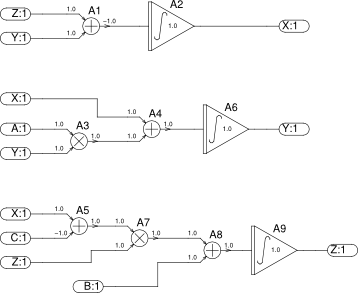
|
| Simulačný model[6][7] |
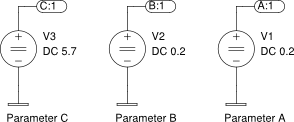
|
| Definícia konštánt a,b,c |
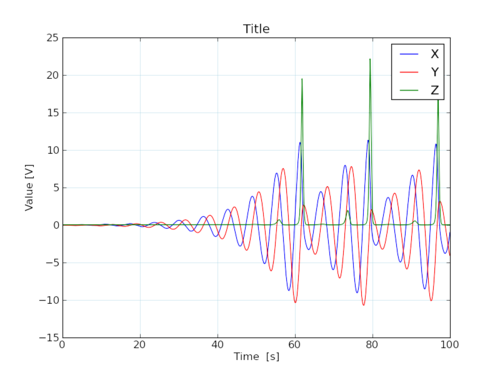
|
| Časový priebeh premenných x, y a z |

|
| Parametrické 2D zobrazenie premenných x a y |
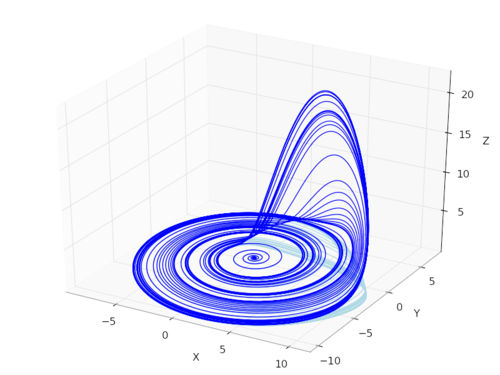
|
| 3D parametrické zobrazenie premenných x,y a z |
Odkazy a literatúra
- ↑ http://en.wikipedia.org/wiki/R%C3%B6ssler_attractor
- ↑ http://www.scholarpedia.org/article/Rossler_attractor
- ↑ http://en.wikipedia.org/wiki/Chaos_theory
- ↑ http://cs.wikipedia.org/wiki/Teorie_chaosu
- ↑ http://sk.wikipedia.org/wiki/Te%C3%B3ria_chaosu
- ↑ http://193.87.70.141/~pf/wiki_upload/sch/0304_rossler.sch
- ↑ http://193.87.70.141/~pf/wiki_upload/pdf/0304_rossler.pdf