Teória grafov: Rozdiel medzi revíziami
| Riadok 27: | Riadok 27: | ||
=Teória grafov= | =Teória grafov= | ||
| + | |||
| + | V matematike a počítačových vedách sa [http://en.wikipedia.org/wiki/Graph_theory teória grafov] zaoberá štúdiom [http://sk.wikipedia.org/wiki/Graf_(matematika) grafov], teda grafických matematických štruktúr používaných na modelovanie vzájomných vzťahov medzi objektami z určitej množiny. Teória grafov je súčasťou diskrétnej matematiky. | ||
| + | |||
==Základné pojmy a charakteristika grafov== | ==Základné pojmy a charakteristika grafov== | ||
| + | |||
| + | {| align="right" | ||
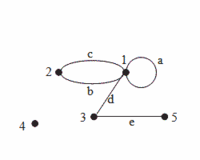
| + | | valign="top" | [[Súbor:Atgathvrp-obr3-priklad_neorientovaneho_grafu.png | thumb | 200px | '''Obr. 3 – Príklad neorientovaného grafu''' <br> | ||
| + | ''a'' je slučka, ''b'' a ''c'' sú rovnobežné hrany, ''4'' je izolovaný vrchol, ''d'' a ''e'' sú susedné (priľahlé) hrany; uzol ''1'' ježí na hranách ''a'', ''b'', ''c'', hrana ''c'' spája uzly ''1'' a ''2''. ]] | ||
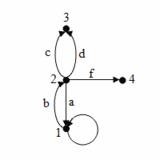
| + | | valign="top" | [[Súbor:Atgathvrp-obr4-priklad_orientovaneho_grafu.png | thumb | 160px | '''Obr. 4 – Príklad orientovaného grafu''' <br> | ||
| + | ''E'' je slučka, ''a'' a ''b'' sú nesúhlasne rovnobežné hrany, ''c'' a ''d'' sú súhlasne rovnobežné hrany. ''2'' je počiatočný a ''4'' koncový uzol hrany ''f''.]] | ||
| + | |} | ||
| + | |||
| + | V matematike sa pojem ''graf'' používa najčastejšie v zmysle grafického znázornenia určitej funkcie , napr. y=f(2x+3). Grafy, ktoré sú objektom štúdia teórie grafov sú však svojou povahou veľmi vzdialené od grafov funkcií. Sú to objekty tvorené určitou množinou bodov a čiar, ktoré tieto body spájajú na základe určitých pravidiel. Graf môžu tvoriť napr. mestá pospájané železnicou, rôzne miesta prepojené mostami ale aj elektrické siete alebo chemické zlúčeniny. | ||
| + | |||
| + | K tomu, aby bol zadaný [http://en.wikipedia.org/wiki/Graph_(mathematics) graf] (označíme ho ''φ'') je treba, aby boli dané dve množiny: množina ''vrcholov V'' (predtým zmieňované body v grafe) a množina ''hrán H'' (zmienené čiary). Vo väčšine prípadov sú obe množiny konečné, avšak nie je to nutná podmienka existencie grafu. Graf potom zapisujeme ako ''φ=VH'', prípadne ''φ=(V,H)''. | ||
| + | |||
| + | |||
==Základné druhy grafových štruktúr== | ==Základné druhy grafových štruktúr== | ||
==Typy problémov riešených pomocou teórie grafov== | ==Typy problémov riešených pomocou teórie grafov== | ||
Verzia zo dňa a času 14:47, 22. január 2010
Obsah
Teória grafov
V matematike a počítačových vedách sa teória grafov zaoberá štúdiom grafov, teda grafických matematických štruktúr používaných na modelovanie vzájomných vzťahov medzi objektami z určitej množiny. Teória grafov je súčasťou diskrétnej matematiky.
Základné pojmy a charakteristika grafov
V matematike sa pojem graf používa najčastejšie v zmysle grafického znázornenia určitej funkcie , napr. y=f(2x+3). Grafy, ktoré sú objektom štúdia teórie grafov sú však svojou povahou veľmi vzdialené od grafov funkcií. Sú to objekty tvorené určitou množinou bodov a čiar, ktoré tieto body spájajú na základe určitých pravidiel. Graf môžu tvoriť napr. mestá pospájané železnicou, rôzne miesta prepojené mostami ale aj elektrické siete alebo chemické zlúčeniny.
K tomu, aby bol zadaný graf (označíme ho φ) je treba, aby boli dané dve množiny: množina vrcholov V (predtým zmieňované body v grafe) a množina hrán H (zmienené čiary). Vo väčšine prípadov sú obe množiny konečné, avšak nie je to nutná podmienka existencie grafu. Graf potom zapisujeme ako φ=VH, prípadne φ=(V,H).